如果你也在 怎样代写数值分析numerical analysis这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。数值分析numerical analysis是研究使用数值逼近(相对于符号操作)来解决数学分析问题的算法(有别于离散数学)。数值分析在工程和物理科学的所有领域都有应用,在21世纪还包括生命科学和社会科学、医学、商业甚至艺术领域。
数值分析numerical analysis目前计算能力的增长使得更复杂的数值分析得以使用,在科学和工程中提供详细和现实的数学模型。数值分析的例子包括:天体力学中的常微分方程(预测行星、恒星和星系的运动),数据分析中的数值线性代数,以及用于模拟医学和生物学中活细胞的随机微分方程和马尔科夫链。
my-assignmentexpert™ 数值分析numerical analysis作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的数值分析numerical analysis作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此数值分析numerical analysis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数值分析numerical anaysis代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种数值分析numerical analysis相关的作业也就用不着 说。
我们提供的数值分析numerical analysis及其相关学科的代写,服务范围广, 其中包括但不限于:
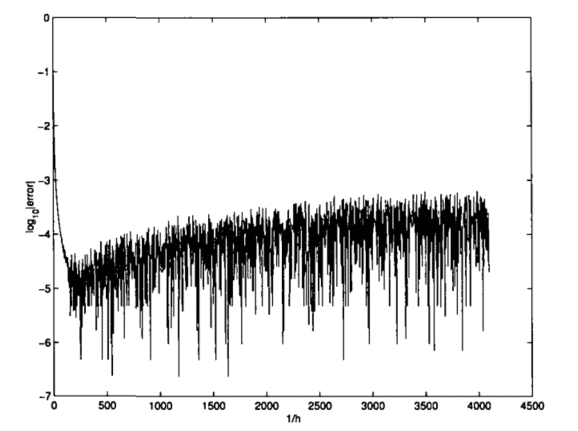
数学代写|数值分析代写numerical analysis代考|HORNER’S RULE AND NESTED MULTIPLICATION
In Chapter 1 we devoted some time to the construction of polynomial approximations to given functions. It might be good if we discussed the best way to evaluate those approximations efficiently; hence this section.
The most efficient way to evaluate a polynomial is by nested multiplication. If we have
$$
p_{n}(x)=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}
$$
then we factor out each power of $x$ as far as it will go, thus getting
$$
p_{n}(x)=a_{0}+x\left(a_{1}+x\left(a_{2}+\cdots+x\left(a_{n-1}+a_{n} x\right) \cdots\right)\right) \text {. }
$$
Computation with the second form of the polynomial will take $n+1$ multiplications and $n$ additions. Computation with the first form will take the same amount of work, plus the cost of forming the powers $x^{2}, x^{3}, \ldots, x^{n}$.
For example, we could write
$$
q(x)=1+x+3 x^{2}-6 x^{3}
$$
as
$$
q(x)=1+x(1+x(3-6 x)) .
$$
数学代写|数值分析代写numerical analysis代考|DIFFERENCE APPROXIMATIONS TO THE DERIVATIVE
One of the simplest uses of Taylor’s Theorem as a means of constructing approximations involves the use of difference quotients to approximate the derivative of a known function $f$. Intuitively, this is obvious from the definition of the derivative:
$$
f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \Rightarrow f^{\prime}(x) \approx \frac{f(x+h)-f(x)}{h} .
$$
The challenge for us is to make this vague statement more precise (just how accurate is this approximation, in terms of the parameter $h$ ?) and to see if anything better (more accurate) can be found.
We determine the accuracy of the approximation by a very simple computation involving Taylor’s Theorem:
$$
f^{\prime}(x)-\frac{f(x+h)-f(x)}{h}=f^{\prime}(x)-\frac{h f^{\prime}(x)+\frac{1}{2} h^{2} f^{\prime \prime}\left(\xi_{x, h}\right)}{h}=-\frac{1}{2} h f^{\prime \prime}\left(\xi_{x, h}\right)
$$
so that we have
$$
f^{\prime}(x)-\frac{f(x+h)-f(x)}{h}=-\frac{1}{2} h f^{\prime \prime}\left(\xi_{x, h}\right)=\mathcal{O}(h)
$$
Thus the error is roughly proportional to the parameter $h$.
Can we do better? Yes, and the improvement does not take a lot of work. Consider the two Taylor expansions:
$$
f(x+h)=f(x)+h f^{\prime}(x)+\frac{1}{2} h^{2} f^{\prime \prime}(x)+\frac{1}{6} h^{3} f^{\prime \prime \prime}\left(\xi_{1}\right)
$$
and
$$
f(x-h)=f(x)-h f^{\prime}(x)+\frac{1}{2} h^{2} f^{\prime \prime}(x)-\frac{1}{6} h^{3} f^{\prime \prime \prime}\left(\xi_{2}\right)
$$
Now subtract these to get
$$
f(x+h)-f(x-h)=2 h f^{\prime}(x)+\frac{1}{6} h^{3} f^{\prime \prime \prime}\left(\xi_{1}\right)+\frac{1}{6} h^{3} f^{\prime \prime \prime}\left(\xi_{2}\right)
$$
We can solve this for $f^{\prime}(x)$ to get
$$
f^{\prime}(x)=\frac{f(x+h)-f(x-h)}{2 h}-\frac{1}{6} h^{2} \frac{f^{\prime \prime \prime}\left(\xi_{1}\right)+f^{\prime \prime \prime}\left(\xi_{2}\right)}{2}
$$
or, using the Discrete Average Value Theorem,
$$
f^{\prime}(x)=\frac{f(x+h)-f(x-h)}{2 h}-\frac{1}{6} h^{2} f^{\prime \prime \prime}\left(\xi_{x, h}\right)
$$
数学代写|数值分析代写NUMERICAL ANALYSIS代考|APPLICATION: EULER’S METHOD FOR INITIAL VALUE PROBLEMS
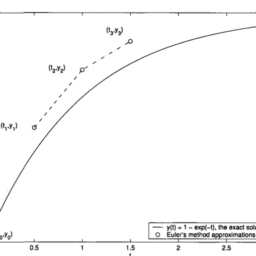
One immediate application of difference methods for approximating derivatives is the approximate solution of initial value problems for ordinary differential equations. The usual general form of such a problem is
$$
y^{\prime}=f(t, y), \quad y\left(t_{0}\right)=y_{0},
$$
where $f$ is a known function of $t$ and $y$, and $t_{0}$ and $y_{0}$ are given values. The object in solving this problem is to find $y$ as a function of $t$; in the usual sophomore-level course in ordinary differential equations, the student learns a number of techniques for analytically solving (2.8), based on assuming any one of a number of special forms for $f$. Here we will use one of our derivative approximations to construct a method for approximately solving (2.8).
We use (2.1) to replace the derivative in (2.8):
$$
\frac{y(t+h)-y(t)}{h}=f(t, y(t))+\frac{1}{2} h y^{\prime \prime}\left(t_{h}\right)
$$
which can be simplified slightly to become
$$
y(t+h)=y(t)+h f(t, y(t))+\frac{1}{2} h^{2} y^{\prime \prime}\left(t_{h}\right) .
$$
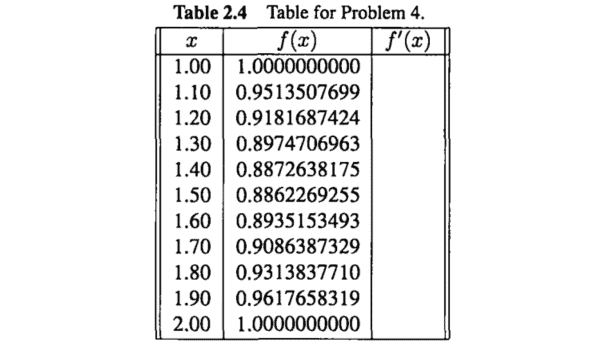
数值分析代写
数学代写|数值分析代写NUMERICAL ANALYSIS代考|HORNER’S RULE AND NESTED MULTIPLICATION
在第 1 章中,我们花了一些时间来构造给定函数的多项式逼近。如果我们讨论有效评估这些近似值的最佳方法可能会很好;因此本节。
评估多项式的最有效方法是嵌套乘法。如果我们有
pn(X)=一种0+一种1X+一种2X2+⋯+一种nXn
然后我们分解出每个幂X尽其所能,从而得到
pn(X)=一种0+X(一种1+X(一种2+⋯+X(一种n−1+一种nX)⋯)).
使用多项式的第二种形式进行计算n+1乘法和n补充。第一种形式的计算将花费相同的工作量,加上形成幂的成本X2,X3,…,Xn.
例如,我们可以写
q(X)=1+X+3X2−6X3
作为
q(X)=1+X(1+X(3−6X)).
数学代写|数值分析代写NUMERICAL ANALYSIS代考|DIFFERENCE APPROXIMATIONS TO THE DERIVATIVE
泰勒定理作为构造近似方法的最简单用途之一涉及使用差商来近似已知函数的导数F. 直观地说,这从导数的定义中是显而易见的:
F′(X)=林H→0F(X+H)−F(X)H⇒F′(X)≈F(X+H)−F(X)H.
我们面临的挑战是使这个模糊的陈述更准确j在s吨H这在一种CC在r一种吨和一世s吨H一世s一种ppr这X一世米一种吨一世这n,一世n吨和r米s这F吨H和p一种r一种米和吨和r$H$?看看有没有更好的米这r和一种CC在r一种吨和能够被找到的。
我们通过涉及泰勒定理的非常简单的计算来确定近似的准确性:
F′(X)−F(X+H)−F(X)H=F′(X)−HF′(X)+12H2F′′(XX,H)H=−12HF′′(XX,H)
所以我们有
F′(X)−F(X+H)−F(X)H=−12HF′′(XX,H)=这(H)
因此误差与参数大致成正比H.
我们能做得更好吗?是的,改进并不需要很多工作。考虑两个泰勒展开式:
F(X+H)=F(X)+HF′(X)+12H2F′′(X)+16H3F′′′(X1)
和
F(X−H)=F(X)−HF′(X)+12H2F′′(X)−16H3F′′′(X2)
现在减去这些得到
F(X+H)−F(X−H)=2HF′(X)+16H3F′′′(X1)+16H3F′′′(X2)
我们可以解决这个问题F′(X)要得到
F′(X)=F(X+H)−F(X−H)2H−16H2F′′′(X1)+F′′′(X2)2
或者,使用离散平均值定理,
F′(X)=F(X+H)−F(X−H)2H−16H2F′′′(XX,H)
数学代写|数值分析代写NUMERICAL ANALYSIS代考|APPLICATION: EULER’S METHOD FOR INITIAL VALUE PROBLEMS
用于逼近导数的差分方法的一种直接应用是常微分方程初值问题的近似解。这种问题的一般一般形式是
是′=F(吨,是),是(吨0)=是0,
在哪里F是一个已知函数吨和是, 和吨0和是0是给定的值。解决这个问题的目的是找到是作为一个函数吨; 在通常的二年级常微分方程课程中,学生学习了许多解析求解的技术2.8,基于假设任何一种特殊形式F. 在这里,我们将使用我们的一个导数近似来构造一种近似求解的方法2.8.
我们用2.1替换导数2.8:
是(吨+H)−是(吨)H=F(吨,是(吨))+12H是′′(吨H)
可以稍微简化为
是(吨+H)=是(吨)+HF(吨,是(吨))+12H2是′′(吨H).

数学代写|数值分析代写numerical analysis代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。