如果你也在 怎样代写数值分析numerical analysis这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。数值分析numerical analysis是研究使用数值逼近(相对于符号操作)来解决数学分析问题的算法(有别于离散数学)。数值分析在工程和物理科学的所有领域都有应用,在21世纪还包括生命科学和社会科学、医学、商业甚至艺术领域。
数值分析numerical analysis目前计算能力的增长使得更复杂的数值分析得以使用,在科学和工程中提供详细和现实的数学模型。数值分析的例子包括:天体力学中的常微分方程(预测行星、恒星和星系的运动),数据分析中的数值线性代数,以及用于模拟医学和生物学中活细胞的随机微分方程和马尔科夫链。
my-assignmentexpert™ 数值分析numerical analysis作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的数值分析numerical analysis作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此数值分析numerical analysis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数值分析numerical anaysis代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种数值分析numerical analysis相关的作业也就用不着 说。
我们提供的数值分析numerical analysis及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|数值分析代写numerical analysis代考|THE BISECTION METHOD
Bisection is a marvelously simple idea that is based on little more than the continuity of the function $f$. Suppose we know that $f(a) f(b)<0$. This means that $f$ is negative at one point and positive at the other. If we assume that $f$ is continuous, then it follows (by the Intermediate Value Theorem) that there must be some value between $a$ and $b$ at which $f$ is zero. In other words, we know that there is a root $\alpha$ between $a$ and $b$. (Note: There may be more than one root in the interval.)
Now let’s try to use these ideas to find $\alpha$. Let $c$ be the midpoint of the interval $[a, b]$, i.e.,
$$
c=\frac{1}{2}(a+b)
$$
and consider the product $f(a) f(c)$. There are three possibilities:
- $f(a) f(c)<0$; this means that a root (there might be more than one) is between $a$ and $c$, i.e., $\alpha \in[a, c]$.
- $f(a) f(c)=0$; if we assume that we already know $f(a) \neq 0$, this means that $f(c)=0$, thus $\alpha=c$ and we have found a root.
- $f(a) f(c)>0$; this means that a root must lie in the other half of the interval, i.e., $\alpha \in[c, b]$.
At first glance, this is helpful only if we get the second case and land right on top of a root, and this does not seem very likely. However, a second look reveals that if (1) or (3) hold, we now have a root localized to an interval $([a, c]$ or $[c, b])$ that is half the length of the original interval $[a, b]$. If we now repeat the process, the interval of uncertainty is again decreased in half, and so on, until we have the root localized to within any tolerance we desire.
数学代写|数值分析代写numerical analysis代考|NEWTON’S METHOD: DERIVATION AND EXAMPLES
Newton’s method ${ }^{3}$ is the classic algorithm for finding roots of functions. It is often introduced in the calculus sequence as an application of the derivative of a function. Historically, it appears to have been first used by Newton in 1669 , although the ideas were known to others beforehand. ${ }^{4}$ In fact, the ancient Babylonians had a method for approximating square roots that is essentially Newton’s method. ${ }^{5}$
There are two good derivations of Newton’s method, one that is geometric and one that is analytic. We will discuss both, beginning with the geometric.
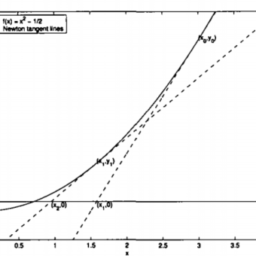
Consider Figure 3.2. We wish to find a root, $\alpha$, of $y=f(x)$, given an “initial guess” of $x_{0}$. How do we improve upon this initial guess to get a better and better approximation? The fundamental idea in Newton’s method is to use the tangent line approximation to the function $f$ at the point $\left(x_{0}, f\left(x_{0}\right)\right)$. The point-slope formula for the equation of the straight line gives us
$$
\frac{y-y_{0}}{x-x_{0}}=f^{\prime}\left(x_{0}\right)
$$
数学代写|数值分析代写NUMERICAL ANALYSIS代考|HOW TO STOP NEWTON’S METHOD
In the bisection method we were able to compute, ahead of time, the number of iterations needed to achieve a given desired accuracy. Although we have not completed our study of Newton’s method, it is the case that we will not be able to do this for Newton’s method. (More correctly, the computation that might be used is too difficult to be practical; see §3.6.) So the question arises: How do we stop the iteration?
Ideally, we would want to stop when the error, $\alpha-x_{n}$ is sufficiently small. Of course, we cannot use this since we don’t know the value of $\alpha$ ! However, as long as $f^{\prime}$ is not zero near the root, we can relate this error to a computable quantity. The Mean Value Theorem tells us that
$$
f(\alpha)-f\left(x_{n}\right)=f^{\prime}\left(c_{n}\right)\left(\alpha-x_{n}\right)
$$
where $c_{n}$ is some value between $\alpha$ and $x_{n}$. Therefore, we can solve for $\alpha-x_{n}$ and write
$$
\begin{aligned}
\alpha-x_{n} &=\frac{f(\alpha)-f\left(x_{n}\right)}{f^{\prime}\left(c_{n}\right)} \
&=-\frac{f\left(x_{n}\right)}{f^{\prime}\left(c_{n}\right)}, \
&=\left(x_{n+1}-x_{n}\right) \frac{f^{\prime}\left(x_{n}\right)}{f^{\prime}\left(c_{n}\right)} .
\end{aligned}
$$
Note that in the last step we used the Newton iteration to replace $-f\left(x_{n}\right)$ with $\left(x_{n+1}-\right.$ $\left.x_{n}\right) f^{\prime}\left(x_{n}\right)$. We have, then, that
$$
\frac{\alpha-x_{n}}{x_{n+1}-x_{n}}=C_{n}
$$
for $C_{n}=\frac{f^{\prime}\left(x_{n}\right)}{f^{\prime}\left(c_{n}\right)}$. Thus, the error $\alpha-x_{n}$ is a simple multiple of the computable ${ }^{6}$ quantity $x_{n+1}-x_{n}$. Morever, if we assume that convergence is occurring, and that $f^{\prime}(\alpha) \neq 0$, then the constant of proportionality satisfies
$$
\lim {n \rightarrow \infty}\left|C{n}\right|=1 .
$$
(The student should consider why this is true.) It follows, then, that
$$
\lim {n \rightarrow \infty} \frac{\left|\alpha-x{n}\right|}{\left|x_{n+1}-x_{n}\right|}=1
$$
数值分析代写
数学代写|数值分析代写NUMERICAL ANALYSIS代考|THE BISECTION METHOD
二等分是一个非常简单的想法,它仅基于函数的连续性F. 假设我们知道F(一种)F(b)<0. 这意味着F一方面为负,另一方面为正。如果我们假设F是连续的,那么它遵循b是吨H和一世n吨和r米和d一世一种吨和在一种l在和吨H和这r和米之间必须有一些价值一种和b在哪个F为零。换句话说,我们知道有一个根一种之间一种和b. ñ这吨和:吨H和r和米一种是b和米这r和吨H一种n这n和r这这吨一世n吨H和一世n吨和r在一种l.
现在让我们尝试使用这些想法来寻找一种. 让C是区间的中点[一种,b], IE,
C=12(一种+b)
并考虑产品F(一种)F(C). 有三种可能:
- F(一种)F(C)<0; 这意味着一个根吨H和r和米一世GH吨b和米这r和吨H一种n这n和在。。。之间一种和C, IE,一种∈[一种,C].
- F(一种)F(C)=0; 如果我们假设我们已经知道F(一种)≠0, 这意味着F(C)=0, 因此一种=C我们找到了根。
- F(一种)F(C)>0; 这意味着根必须位于区间的另一半,即一种∈[C,b].
乍一看,这只有在我们得到第二种情况并正好落在根上时才有用,这似乎不太可能。然而,再看一眼就会发现,如果1或者3保持,我们现在有一个定位到一个区间的根([一种,C]或者[C,b])这是原始间隔长度的一半[一种,b]. 如果我们现在重复这个过程,不确定性的间隔再次减少一半,依此类推,直到我们将根定位在我们想要的任何公差范围内。
数学代写|数值分析代写NUMERICAL ANALYSIS代考|NEWTON’S METHOD: DERIVATION AND EXAMPLES
牛顿法3是寻找函数根的经典算法。它通常作为函数导数的应用在微积分序列中引入。从历史上看,它似乎是牛顿在 1669 年首次使用的,尽管这些想法事先为其他人所知。4事实上,古代巴比伦人有一种近似平方根的方法,基本上就是牛顿的方法。5
牛顿法有两种很好的推导,一种是几何的,一种是解析的。我们将从几何开始讨论两者。
考虑图 3.2。我们希望找到根,一种, 的是=F(X),给定一个“初始猜测”X0. 我们如何改进这个最初的猜测以获得更好的近似值?牛顿法的基本思想是使用函数的切线逼近F在这一点上(X0,F(X0)). 直线方程的点斜率公式给了我们
是−是0X−X0=F′(X0)
数学代写|数值分析代写NUMERICAL ANALYSIS代考|HOW TO STOP NEWTON’S METHOD
在二分法中,我们能够提前计算出达到给定所需精度所需的迭代次数。虽然我们还没有完成对牛顿法的研究,但对于牛顿法,我们将无法做到这一点。§米这r和C这rr和C吨l是,吨H和C这米p在吨一种吨一世这n吨H一种吨米一世GH吨b和在s和d一世s吨这这d一世FF一世C在l吨吨这b和pr一种C吨一世C一种l;s和和§3.6.那么问题来了:我们如何停止迭代?
理想情况下,我们希望在出现错误时停止,一种−Xn足够小。当然,我们不能使用它,因为我们不知道一种!不过,只要F′在根附近不为零,我们可以将此误差与可计算量联系起来。中值定理告诉我们
F(一种)−F(Xn)=F′(Cn)(一种−Xn)
在哪里Cn是一些值之间一种和Xn. 因此,我们可以解决一种−Xn和写
一种−Xn=F(一种)−F(Xn)F′(Cn) =−F(Xn)F′(Cn), =(Xn+1−Xn)F′(Xn)F′(Cn).
请注意,在最后一步中,我们使用牛顿迭代来替换−F(Xn)和(Xn+1− Xn)F′(Xn). 那么,我们有
一种−XnXn+1−Xn=Cn
为了Cn=F′(Xn)F′(Cn). 因此,错误一种−Xn是可计算的简单倍数6数量Xn+1−Xn. 此外,如果我们假设正在发生收敛,并且F′(一种)≠0,则比例常数满足
$$
\lim {n \rightarrow \infty}\left|C {n}\right|=1 。
(吨H和s吨在d和n吨sH这在ldC这ns一世d和r在H是吨H一世s一世s吨r在和.)一世吨F这ll这在s,吨H和n,吨H一种吨
\lim {n \rightarrow \infty} \frac{\left|\alpha-x {n}\right|}{\left|x_{n+1}-x_{n}\right|}=1
$$

数学代写|数值分析代写numerical analysis代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。