如果你也在 怎样代写数值分析numerical analysis这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。数值分析numerical analysis是研究使用数值逼近(相对于符号操作)来解决数学分析问题的算法(有别于离散数学)。数值分析在工程和物理科学的所有领域都有应用,在21世纪还包括生命科学和社会科学、医学、商业甚至艺术领域。
数值分析numerical analysis目前计算能力的增长使得更复杂的数值分析得以使用,在科学和工程中提供详细和现实的数学模型。数值分析的例子包括:天体力学中的常微分方程(预测行星、恒星和星系的运动),数据分析中的数值线性代数,以及用于模拟医学和生物学中活细胞的随机微分方程和马尔科夫链。
my-assignmentexpert™ 数值分析numerical analysis作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的数值分析numerical analysis作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此数值分析numerical analysis作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数值分析numerical anaysis代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种数值分析numerical analysis相关的作业也就用不着 说。
我们提供的数值分析numerical analysis及其相关学科的代写,服务范围广, 其中包括但不限于:

数学代写|数值分析代写numerical analysis代考|THE INITIAL VALUE PROBLEM: BACKGROUND
Consider the ordinary differential equation
$$
\frac{d y}{d t}=f(t, y(t)), \quad y\left(t_{0}\right)=y_{0},
$$
where $f$ is a function from $\mathbb{R}^{N+1}$ into $\mathbb{R}^{N}$ for some $N>0$ (if $N=1$, then we have a scalar equation; otherwise, a vector equation); $t_{0}$ is a given scalar value, often taken to be $t_{0}=0$, and known as the initial point; and $y_{0}$ is a known vector in $\mathbb{R}^{N}$, known as the initial value. We want to find the unknown function $y(t)$, which solves $(6.4)$ in the sense that
$$
y^{\prime}(t)-f(t, y(t))=0
$$
for all $t>t_{0}$, and $y\left(t_{0}\right)=y_{0}$.
Some examples will be useful at this point.
EXAMPLE 6.1
Consider the simple problem
$$
y^{\prime}=-2 t y, \quad y(0)=1 .
$$
Here $f(t, y)=-2 t y, t_{0}=0, y_{0}=1$, and we can apply methods from a standard ordinary differential equations (ODE) course to show that $y(t)=e^{-t^{2}}$ is the solution.
数学代写|数值分析代写numerical analysis代考|EULER’S METHOD
Euler’s method is the natural starting point for any discussion of numerical methods for IVPs. Although it is not the most accurate of the methods we study, it is by far the simplest, and much of what we learn from analyzing Euler’s method in detail carries over to other methods without a lot of difficulty. Even though we treated Euler’s method in Chapter 2, we are going to cover it again here, but this time more fully.
There are two main derivations; one is geometric, the other is analytic, and a third derivation (the one we used in Chapter 2 ) is given in $\S 6.4$. We start with the geometric derivation.
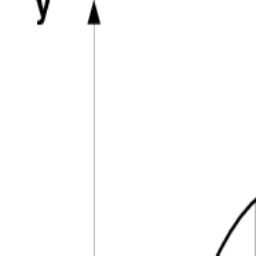
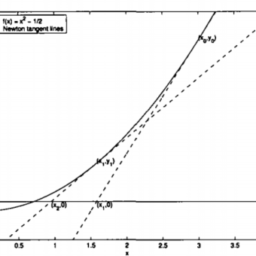
Consider Figure 6.1. This shows the graph of the solution
$y(t)$ to the initial value problem
$$
y^{\prime}=f(t, y), \quad y\left(t_{0}\right)=y_{0},
$$
near the initial point $t_{0}$. All we know about $y$ is that it passes through the point $\left(t_{0}, y_{0}\right)=$ $(0,0)$, and that it has slope $f\left(t_{0}, y_{0}\right)$ (why?) at that point. We therefore can approximate $y(t+h)$ for some small $h$ by using the tangent line approximation:
$$
y\left(t_{0}+h\right) \approx y\left(t_{0}\right)+h f\left(t_{0}, y\left(t_{0}\right)\right)
$$
For small values of $h$ this will be a decent approximation, and if we define the next point in our grid by $t_{1}=t_{0}+h$, then it is very natural to extend $(6.10)$ to get
$$
y\left(t_{1}+h\right) \approx y\left(t_{1}\right)+h f\left(t_{1}, y\left(t_{1}\right)\right),
$$
or, more generally,
$$
y\left(t_{n}+h\right) \approx y\left(t_{n}\right)+h f\left(t_{n}, y\left(t_{n}\right)\right)
$$
The numerical method is then defined from (6.12) according to
$$
y_{n+1}=y_{n}+h f\left(t_{n}, y_{n}\right)
$$
with $y_{0}$ given and $y_{n} \approx y\left(t_{n}\right)$.
数学代写|数值分析代写NUMERICAL ANALYSIS代考|ANALYSIS OF EULER’S METHOD
In this section we will prove two results that establish the convergence and error estimate for Euler’s method. We provide a fair amount of detail in this section, in order to avoid going into so much detail with more sophisticated methods that we will derive later. Throughout the section we are concerned with the approximate solution, via Euler’s method, of the initial value problem
$$
y^{\prime}=f(t, y), \quad y\left(t_{0}\right)=y_{0} .
$$
The first theorem shows that Euler’s method is, indeed, first-order accurate.
Theorem 6.3 (Error Estimate for Euler’s Method, version I) Let $f$ be Lipschitz continuous, with constant $K$, and assume that the solution $y \in C^{2}\left(\left[t_{0}, T\right]\right)$ for some $T>t_{0}$. Then
$$
\max {t{k} \leq T}\left|y\left(t_{k}\right)-y_{k}\right| \leq C_{0}\left|y\left(t_{0}\right)-y_{0}\right|+C h\left|y^{\prime \prime}\right|{\infty,\left[t{0}, T\right]}
$$
where
$$
C_{0}=e^{K\left(T-t_{0}\right)}
$$
and
$$
C=\frac{e^{K\left(T-t_{0}\right)}-1}{2 K}
$$
Proof: The key element in the proof of this result is the fact that the exact solution satisfies the same relationship as does the approximate solution, except for the addition of a remainder term. Thus we have (from (6.13) and (6.14)),
$$
\begin{aligned}
y\left(t_{n+1}\right) &=y\left(t_{n}\right)+h f\left(t_{n}, y\left(t_{n}\right)\right)+\frac{1}{2} h^{2} y^{\prime \prime}\left(\theta_{n}\right) \
y_{n+1} &=y_{n}+h f\left(t_{n}, y_{n}\right)
\end{aligned}
$$
which we subtract to get
$$
y\left(t_{n+1}\right)-y_{n+1}=y\left(t_{n}\right)-y_{n}+h f\left(t_{n}, y\left(t_{n}\right)\right)-h f\left(t_{n}, y_{n}\right)+\frac{1}{2} h^{2} y^{\prime \prime}\left(\theta_{n}\right) .
$$
Take absolute values and apply the Lipschitz continuity of $f$ to get
$$
\left|y\left(t_{n+1}\right)-y_{n+1}\right| \leq\left|y\left(t_{n}\right)-y_{n}\right|+K h\left|y\left(t_{n}\right)-y_{n}\right|+\frac{1}{2} h^{2}\left|y^{\prime \prime}\left(\theta_{n}\right)\right|
$$
which we write as
$$
e_{n+1} \leq \gamma e_{n}+R_{n}
$$
where $e_{n}=\left|y\left(t_{n}\right)-y_{n}\right|, \gamma=1+K h$, and $R_{n}=\frac{1}{2} h^{2}\left|y^{\prime \prime}\left(\theta_{n}\right)\right|$, for notational simplicity. This is a simple recursive inequality, which we can “solve” as follows. We have
$$
\begin{aligned}
&e_{1} \leq \gamma e_{0}+R_{0} \
&e_{2} \leq \gamma e_{1}+R_{1} \leq \gamma^{2} e_{0}+\gamma R_{0}+R_{1} \
&e_{3} \leq \gamma e_{2}+R_{2} \leq \gamma^{3} e_{0}+\gamma^{2} R_{0}+\gamma R_{1}+R_{2}
\end{aligned}
$$
and so on. An inductive argument can be applied to get the general result
$$
e_{n} \leq \gamma^{n} e_{0}+\frac{1}{2} h^{2} \sum_{k=0}^{n-1} \gamma^{k}\left|y^{\prime \prime}\left(\theta_{n-1-k}\right)\right|
$$
数值分析代写
数学代写|数值分析代写NUMERICAL ANALYSIS代考|THE INITIAL VALUE PROBLEM: BACKGROUND
考虑常微分方程
$$
\frac{d y}{d t}=f(t, y(t)), \quad y\left(t_{0}\right)=y_{0},
$$
where $f$ is a function from $\mathbb{R}^{N+1}$ into $\mathbb{R}^{N}$ for some $N>0$ (if $N=1$, then we have a scalar equation; otherwise, a vector equation); $t_{0}$ is a given scalar value, often taken to be $t_{0}=0$, and known as the initial point; and $y_{0}$ is a known vector in $\mathbb{R}^{N}$, known as the initial value. We want to find the unknown function $y(t)$, which solves $(6.4)$ in the sense that
$$
y^{\prime}(t)-f(t, y(t))=0
$$
for all $t>t_{0}$, and $y\left(t_{0}\right)=y_{0}$.
在这一点上,一些示例将很有用。
例 6.1
考虑一个简单的问题
是′=−2吨是,是(0)=1.
这里F(吨,是)=−2吨是,吨0=0,是0=1, 我们可以应用标准常微分方程的方法这D和当然要表明是(吨)=和−吨2是解决方案。
数学代写|数值分析代写NUMERICAL ANALYSIS代考|EULER’S METHOD
欧拉方法是任何讨论 IVP 数值方法的自然起点。虽然它不是我们研究的方法中最准确的,但它是迄今为止最简单的,而且我们从详细分析欧拉方法中学到的大部分内容可以毫无困难地应用于其他方法。尽管我们在第 2 章中讨论了欧拉方法,但我们将在这里再次介绍它,但这次更全面。
有两个主要推导;一个是几何的,另一个是解析的,第三个推导吨H和这n和在和在s和d一世nCH一种p吨和r2给出在§§6.4. 我们从几何推导开始。
考虑图 6.1。这显示了解决方案的图表是
$y(t)$ to the initial value problem
$$
y^{\prime}=f(t, y), \quad y\left(t_{0}\right)=y_{0},
$$
near the initial point $t_{0}$. All we know about $y$ is that it passes through the point $\left(t_{0}, y_{0}\right)=$ $(0,0)$, and that it has slope $f\left(t_{0}, y_{0}\right)$ (why?) at that point. We therefore can approximate $y(t+h)$ for some small $h$ by using the tangent line approximation:
$$
y\left(t_{0}+h\right) \approx y\left(t_{0}\right)+h f\left(t_{0}, y\left(t_{0}\right)\right)
$$
For small values of $h$ this will be a decent approximation, and if we define the next point in our grid by $t_{1}=t_{0}+h$, then it is very natural to extend $(6.10)$ to get
$$
y\left(t_{1}+h\right) \approx y\left(t_{1}\right)+h f\left(t_{1}, y\left(t_{1}\right)\right),
$$
or, more generally,
$$
y\left(t_{n}+h\right) \approx y\left(t_{n}\right)+h f\left(t_{n}, y\left(t_{n}\right)\right)
$$
The numerical method is then defined from (6.12) according to
$$
y_{n+1}=y_{n}+h f\left(t_{n}, y_{n}\right)
$$
with $y_{0}$ given and $y_{n} \approx y\left(t_{n}\right)$.
数学代写|数值分析代写NUMERICAL ANALYSIS代考|ANALYSIS OF EULER’S METHOD
在本节中,我们将证明建立 Euler 方法的收敛和误差估计的两个结果。我们在本节中提供了相当多的细节,以避免使用我们稍后将推导出的更复杂的方法进入如此多的细节。在本节中,我们关注的是通过欧拉方法对初值问题的近似解
是′=F(吨,是),是(吨0)=是0.
第一个定理表明,欧拉方法确实是一阶精确的。
定理 6.3(Error Estimate for Euler’s Method, version I) Let $f$ be Lipschitz continuous, with constant $K$, and assume that the solution $y \in C^{2}\left(\left[t_{0}, T\right]\right)$ for some $T>t_{0}$. Then
$$
\max {t{k} \leq T}\left|y\left(t_{k}\right)-y_{k}\right| \leq C_{0}\left|y\left(t_{0}\right)-y_{0}\right|+C h\left|y^{\prime \prime}\right|{\infty,\left[t{0}, T\right]}
$$
where
$$
C_{0}=e^{K\left(T-t_{0}\right)}
$$
and
$$
C=\frac{e^{K\left(T-t_{0}\right)}-1}{2 K}
$$
Proof: The key element in the proof of this result is the fact that the exact solution satisfies the same relationship as does the approximate solution, except for the addition of a remainder term. Thus we have (from (6.13) and (6.14)),
$$
\begin{aligned}
y\left(t_{n+1}\right) &=y\left(t_{n}\right)+h f\left(t_{n}, y\left(t_{n}\right)\right)+\frac{1}{2} h^{2} y^{\prime \prime}\left(\theta_{n}\right) \
y_{n+1} &=y_{n}+h f\left(t_{n}, y_{n}\right)
\end{aligned}
$$
which we subtract to get
$$
y\left(t_{n+1}\right)-y_{n+1}=y\left(t_{n}\right)-y_{n}+h f\left(t_{n}, y\left(t_{n}\right)\right)-h f\left(t_{n}, y_{n}\right)+\frac{1}{2} h^{2} y^{\prime \prime}\left(\theta_{n}\right) .
$$
Take absolute values and apply the Lipschitz continuity of $f$ to get
$$
\left|y\left(t_{n+1}\right)-y_{n+1}\right| \leq\left|y\left(t_{n}\right)-y_{n}\right|+K h\left|y\left(t_{n}\right)-y_{n}\right|+\frac{1}{2} h^{2}\left|y^{\prime \prime}\left(\theta_{n}\right)\right|
$$
which we write as
$$
e_{n+1} \leq \gamma e_{n}+R_{n}
$$
where $e_{n}=\left|y\left(t_{n}\right)-y_{n}\right|, \gamma=1+K h$, and $R_{n}=\frac{1}{2} h^{2}\left|y^{\prime \prime}\left(\theta_{n}\right)\right|$, for notational simplicity. This is a simple recursive inequality, which we can “solve” as follows. We have
$$
\begin{aligned}
&e_{1} \leq \gamma e_{0}+R_{0} \
&e_{2} \leq \gamma e_{1}+R_{1} \leq \gamma^{2} e_{0}+\gamma R_{0}+R_{1} \
&e_{3} \leq \gamma e_{2}+R_{2} \leq \gamma^{3} e_{0}+\gamma^{2} R_{0}+\gamma R_{1}+R_{2}
\end{aligned}
$$
and so on. An inductive argument can be applied to get the general result
$$
e_{n} \leq \gamma^{n} e_{0}+\frac{1}{2} h^{2} \sum_{k=0}^{n-1} \gamma^{k}\left|y^{\prime \prime}\left(\theta_{n-1-k}\right)\right|
$$

数学代写|数值分析代写numerical analysis代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。