如果你也在 怎样代写拓扑学topology这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。拓扑学topology在数学中,拓扑学(来自希腊语中的τόπος,”地方、位置”,和λόγος,”研究”)关注的是几何对象在连续变形下保持的属性,如拉伸、扭曲、皱缩和弯曲;也就是说,在不关闭孔、打开孔、撕裂、粘连或穿过自身的情况下。
拓扑学topology拓扑空间是一个被赋予了结构的集合,称为拓扑,它允许定义子空间的连续变形,以及更广泛地定义所有种类的连续性。欧几里得空间,以及更一般的,公制空间都是拓扑空间的例子,因为任何距离或公制都定义了一个拓扑。拓扑学中所考虑的变形是同构和同形。在这种变形下不变的属性是一种拓扑属性。拓扑属性的基本例子有:维度,它可以区分线和面;紧凑性,它可以区分线和圆;连接性,它可以区分一个圆和两个不相交的圆。
my-assignmentexpert™ 拓扑学topology作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的拓扑学topology作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此拓扑学topology作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的拓扑学topology代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种拓扑学topology相关的作业也就用不着 说。
我们提供的拓扑学topology及其相关学科的代写,服务范围广, 其中包括但不限于:
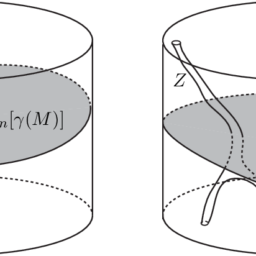
数学代写|拓扑学作业代写topology代考|Tubular neighbourhoods and collars
Let $M \subset \mathbb{R}^{h}$ be a compact boundaryless smooth $m$-manifold. Let $\mathbb{R}^{h}$ be endowed with the standard Riemannian metric $g_{0}$. Let us perform the following construction.
(1) Consider the smooth map
$$
\nu: M \rightarrow \mathfrak{G}{h, h-m} $$ where for every $p \in M, \nu(p)$ is the (matrix corresponding to the) orthogonal space $\left(T{p} M\right)^{\perp}\left(\right.$ with respect to $\left.g_{0}\right)$.
(2) Take the pull-back
$$
\nu^{} \tau_{h, h-m}: \nu^{}\left(\mathcal{V}\left(\mathfrak{G}{h, h-m}\right)\right) \rightarrow M . $$ Every fibre $\nu(p)$ of this vector bundle is endowed with the restriction of $g{0}$. We consider $M \subset \nu^{}\left(\mathcal{V}\left(\mathfrak{G}{h, h-m}\right)\right)$ via the canonical “zero section”. (3) Define the smooth map $$ f{\nu}: \nu^{}\left(\mathcal{V}\left(\mathfrak{G}{h, h-m}\right)\right) \rightarrow \mathbb{R}^{h}, f{\nu}(p, v)=p+v .
$$
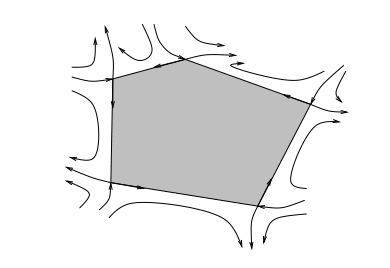
数学代写|拓扑学作业代写topology代考|The “double” of a manifold with boundary
Let $M \subset \mathbb{R}^{h}$ be a compact smooth manifold with $\partial M \neq \emptyset$. The existence of collars suggests a variant in the definition of a nice atlas given in Section 4.11.
Definition 6.5. A nice atlas with collar of $(M, \partial M)$ is of the form
$$
\left{\left(W_{\partial}, \phi_{\partial}\right)\right} \cup\left{\left(W_{j}, \phi_{j}\right)\right}, 1, \ldots, s
$$
where:
(1) $W_{\partial}$ is an open neighbourhood of $\partial M$ and
$$
\phi_{\partial}: W_{\partial} \rightarrow \partial M \times[0,1)
$$
is a diffeomorphism which is equal to the identity on $\partial M$. Define $B_{\partial}:=\phi_{\partial}^{-1}([0,1 / 3))$.
(2) Every $\left(W_{j}, \phi_{j}\right)$ is an normal chart contained in the interior of $M$, and $B_{j} \subset W_{j}$ is defined as for the usual nice atlas.
(3) $\left{B_{\partial}\right} \cup\left{B_{j}\right}$ is an open covering of $M$.
数学代写|拓扑学作业代写TOPOLOGY代考|A fibration theorem
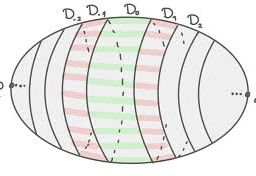
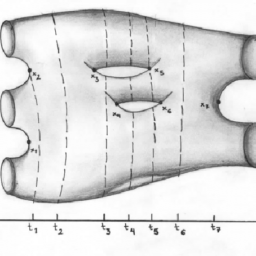
Proposition 6.11 (Fibration theorem). Let $M$ be a compact boundaryless smooth manifold and let $f: M \rightarrow N$ be a surjective submersion to the connected manifold $N$. Let $q_{0} \in N, F=f^{-1}\left(q_{0}\right)$. Then $f$ is a smooth fibre bundle with fibre $F$.
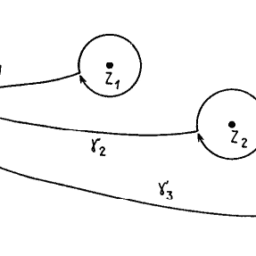
Proof. Let $q_{0} \in N$ and $F=f^{-1}\left(q_{0}\right)$. We know that $F$ is a submanifold of $M$. Fix a tubular neighbourhood $(U, p)$ of $F$ in $M$. Let $D$ be a small open disk in $N$ around $q_{0}$ such that $f^{-1}(D) \subset U$. Define $h: f^{-1}(D) \rightarrow F \times D$, $h(x)=(p(x), f(x))$. Clearly, $f=p_{D} \circ h$, where $p_{D}$ is the projection to $D$. Moreover, $h(x)=(x, 0)$ for every $x \in F$. As $f$ is a submersion, it is easy to verify that the differential of $h$ is invertible on $f^{-1}(D)$ (possibly shrinking $D)$. As $h$ is essentially the identity on $F$ and the fibres are compact, a usual argument (for instance like in the construction of the tubular neighbourhoods) shows that if $D$ is small enough, $h$ is a diffeomorphism and hence a local trivialization of $f$. If $q$ is an arbitrary point of $N$, we can cover a smooth arc joining $q_{0}$ and $q$ in $N$ by a “chain” of similar local trivializations over a chain $D=D_{0}, D_{1}, \ldots, D_{k}$, with $D_{k}$ around $q$, of small disks centred at the arc, $D_{j} \cap D_{j+1} \neq \emptyset$, so that we eventually deduce that the fibre $F^{\prime}$ over $q$ is diffeomorphic to $F$. Finally, we have proved that $f$ is a smooth fibration with fibre $F$.
拓扑学代写
数学代写|拓扑学作业代写TOPOLOGY代考|TUBULAR NEIGHBOURHOODS AND COLLARS
让米⊂RH是一个紧致的无边界光滑米-歧管。让RH被赋予标准黎曼度量G0. 让我们执行以下构造。
1考虑平滑映射
$$
\nu: M \rightarrow \mathfrak{G}{h, h-m} $$ where for every $p \in M, \nu(p)$ is the (matrix corresponding to the) orthogonal space $\left(T{p} M\right)^{\perp}\left(\right.$ with respect to $\left.g_{0}\right)$.
(2) Take the pull-back
$$
\nu^{} \tau_{h, h-m}: \nu^{}\left(\mathcal{V}\left(\mathfrak{G}{h, h-m}\right)\right) \rightarrow M . $$ Every fibre $\nu(p)$ of this vector bundle is endowed with the restriction of $g{0}$. We consider $M \subset \nu^{}\left(\mathcal{V}\left(\mathfrak{G}{h, h-m}\right)\right)$ via the canonical “zero section”. (3) Define the smooth map $$ f{\nu}: \nu^{}\left(\mathcal{V}\left(\mathfrak{G}{h, h-m}\right)\right) \rightarrow \mathbb{R}^{h}, f{\nu}(p, v)=p+v .
$$
数学代写|拓扑学作业代写TOPOLOGY代考|THE “DOUBLE” OF A MANIFOLD WITH BOUNDARY
让米⊂RH是一个紧致光滑流形∂米≠∅. 项圈的存在表明第 4.11 节给出的漂亮图集的定义存在变体。
定义 6.5。一个漂亮的地图集,领子(米,∂米)是形式
\left{\left(W_{\partial}, \phi_{\partial}\right)\right} \cup\left{\left(W_{j}, \phi_{j}\right)\right}, 1 , \ldots, s\left{\left(W_{\partial}, \phi_{\partial}\right)\right} \cup\left{\left(W_{j}, \phi_{j}\right)\right}, 1 , \ldots, s
在哪里:
1 在∂是一个开放的邻域∂米和
φ∂:在∂→∂米×[0,1)
是一个微分同胚,它等于∂米. 定义乙∂:=φ∂−1([0,1/3)).
2每一个(在j,φj)是包含在内部的正常图表米, 和乙j⊂在j被定义为通常的漂亮图集。
3 \left{B_{\partial}\right} \cup\left{B_{j}\right}\left{B_{\partial}\right} \cup\left{B_{j}\right}是一个开覆盖米.
数学代写|拓扑学作业代写TOPOLOGY代考|A FIBRATION THEOREM
提案 6.11F一世br一种吨一世这n吨H和这r和米. 让米是一个紧凑的无边界光滑流形并且让F:米→ñ是连接流形的满射浸没ñ. 让q0∈ñ,F=F−1(q0). 然后F是带有纤维的光滑纤维束F.
证明。. Let $q_{0} \in N$ and $F=f^{-1}\left(q_{0}\right)$. We know that $F$ is a submanifold of $M$. Fix a tubular neighbourhood $(U, p)$ of $F$ in $M$. Let $D$ be a small open disk in $N$ around $q_{0}$ such that $f^{-1}(D) \subset U$. Define $h: f^{-1}(D) \rightarrow F \times D$, $h(x)=(p(x), f(x))$. Clearly, $f=p_{D} \circ h$, where $p_{D}$ is the projection to $D$. Moreover, $h(x)=(x, 0)$ for every $x \in F$. As $f$ is a submersion, it is easy to verify that the differential of $h$ is invertible on $f^{-1}(D)$ (possibly shrinking $D)$. As $h$ is essentially the identity on $F$ and the fibres are compact, a usual argument (for instance like in the construction of the tubular neighbourhoods) shows that if $D$ is small enough, $h$ is a diffeomorphism and hence a local trivialization of $f$. If $q$ is an arbitrary point of $N$, we can cover a smooth arc joining $q_{0}$ and $q$ in $N$ by a “chain” of similar local trivializations over a chain $D=D_{0}, D_{1}, \ldots, D_{k}$, with $D_{k}$ around $q$, of small disks centred at the arc, $D_{j} \cap D_{j+1} \neq \emptyset$, so that we eventually deduce that the fibre $F^{\prime}$ over $q$ is diffeomorphic to $F$. Finally, we have proved that $f$ is a smooth fibration with fibre $F$.

数学代写|拓扑学作业代写TOPOLOGY代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。