如果你也在 怎样代写matlab这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。matlab是由MathWorks公司开发的一种专有的多范式编程语言和数字计算环境。MATLAB允许进行矩阵操作、绘制函数和数据、实现算法、创建用户界面以及与用其他语言编写的程序对接。
matlab尽管MATLAB主要用于数值计算,但一个可选的工具箱使用MuPAD符号引擎,允许访问符号计算能力。一个额外的软件包,Simulink,为动态和嵌入式系统增加了图形化的多域仿真和基于模型的设计。截至2020年,MATLAB在全球拥有超过400万用户。他们来自工程、科学和经济的各种背景。
my-assignmentexpert™ matlab作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的matlab作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此matlab作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的matlab代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种matlab相关的作业也就用不着 说。
我们提供的matlab及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|matlab代写|Introduction
Numerical differentiation deals with the following problem: we are given the function $y=f(x)$ and wish to obtain one of its derivatives at the point $x=x_{k}$. The term “given” means that we either have an algorithm for computing the function, or possess a set of discrete data points $\left(x_{i}, y_{i}\right), i=1,2, \ldots, n$. In either case, we have access to a finite number of $(x, y)$ data pairs from which to compute the derivative. If you suspect by now that numerical differentiation is related to interpolation, you are right-one means of finding the derivative is to approximate the function locally by a polynomial and then differentiate it. An equally effective tool is the Taylor series expansion of $f(x)$ about the point $x_{k}$. The latter has the advantage of providing us with information about the error involved in the approximation.
Numerical differentiation is not a particularly accurate process. It suffers from a conflict between roundoff errors (due to limited machine precision) and errors inherent in interpolation. For this reason, a derivative of a function can never be computed with the same precision as the function itself.
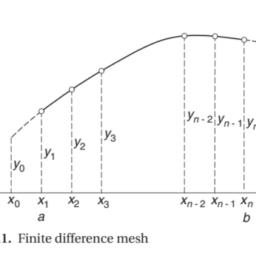
数学代写|matlab代写|Finite Difference Approximations
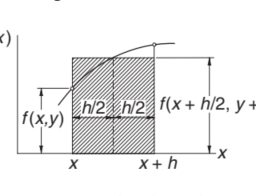
The derivation of the finite difference approximations for the derivatives of $f(x)$ are based on forward and backward Taylor series expansions of $f(x)$ about $x$, such as
$$
f(x+h)=f(x)+h f^{\prime}(x)+\frac{h^{2}}{2 !} f^{\prime \prime}(x)+\frac{h^{3}}{3 !} f^{\prime \prime \prime}(x)+\frac{h^{4}}{4 !} f^{(4)}(x)+\cdots
$$
$$
\begin{aligned}
f(x-h) &=f(x)-h f^{\prime}(x)+\frac{h^{2}}{2 !} f^{\prime \prime}(x)-\frac{h^{3}}{3 !} f^{\prime \prime \prime}(x)+\frac{h^{4}}{4 !} f^{(4)}(x)-\cdots \
f(x+2 h) &=f(x)+2 h f^{\prime}(x)+\frac{(2 h)^{2}}{2 !} f^{\prime \prime}(x)+\frac{(2 h)^{3}}{3 !} f^{\prime \prime \prime}(x)+\frac{(2 h)^{4}}{4 !} f^{(4)}(x)+\cdots \
f(x-2 h) &=f(x)-2 h f^{\prime}(x)+\frac{(2 h)^{2}}{2 !} f^{\prime \prime}(x)-\frac{(2 h)^{3}}{3 !} f^{\prime \prime \prime}(x)+\frac{(2 h)^{4}}{4 !} f^{(4)}(x)-\cdots
\end{aligned}
$$
We also record the sums and differences of the series:
$$
\begin{gathered}
f(x+h)+f(x-h)=2 f(x)+h^{2} f^{\prime \prime}(x)+\frac{h^{4}}{12} f^{(4)}(x)+\cdots \
f(x+h)-f(x-h)=2 h f^{\prime}(x)+\frac{h^{3}}{3} f^{\prime \prime \prime}(x)+\cdots \
f(x+2 h)+f(x-2 h)=2 f(x)+4 h^{2} f^{\prime \prime}(x)+\frac{4 h^{4}}{3} f^{(4)}(x)+\cdots \
f(x+2 h)-f(x-2 h)=4 h f^{\prime}(x)+\frac{8 h^{3}}{3} f^{\prime \prime \prime}(x)+\cdots
\end{gathered}
$$
Note that the sums contain only even derivatives, while the differences retain just the odd derivatives. Equations (a)-(h) can be viewed as simultaneous equations that can be solved for various derivatives of $f(x)$. The number of equations involved and the number of terms kept in each equation depend on the order of the derivative and the desired degree of accuracy.
数学代写|MATLAB代写|Richardson Extrapolation
Richardson extrapolation is a simple method for boosting the accuracy of certain numerical procedures, including finite difference approximations (we will also use it later in numerical integration).
Suppose that we have an approximate means of computing some quantity $G$. Moreover, assume that the result depends on a parameter $h$. Denoting the approximation by $g(h)$, we have $G=g(h)+E(h)$, where $E(h)$ represents the error. Richardson extrapolation can remove the error, provided that it has the form $E(h)=c h^{p}, c$ and $p$ being constants. We start by computing $g(h)$ with some value of $h$, say $h=h_{1}$. In that case we have
$$
G=g\left(h_{1}\right)+c h_{1}^{p}
$$
Then we repeat the calculation with $h=h_{2}$, so that
$$
G=g\left(h_{2}\right)+c h_{2}^{p}
$$
Eliminating $c$ and solving for $G$, we obtain from Eqs. (i) and (j)
$$
G=\frac{\left(h_{1} / h_{2}\right)^{p} g\left(h_{2}\right)-g\left(h_{1}\right)}{\left(h_{1} / h_{2}\right)^{p}-1}
$$
which is the Richardson extrapolation formula. It is common practice to use $h_{2}=h_{1} / 2$, in which case Eq. (5.9a) becomes
$$
G=\frac{2^{p} g\left(h_{1} / 2\right)-g\left(h_{1}\right)}{2^{p}-1}
$$
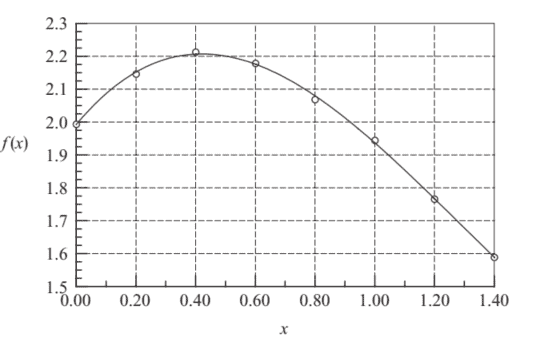
Let us illustrate Richardson extrapolation by applying it to the finite difference approximation of $\left(e^{-x}\right)^{\prime \prime}$ at $x=1$. We work with six-digit precision and utilize the results in Table 5.4. Since the extrapolation works only on the truncation error, we must confine $h$ to values that produce negligible roundoff. Choosing $h_{1}=0.64$ and letting $g(h)$ be the approximation of $f^{\prime \prime}(1)$ obtained with $h$, we get from Table $5.4$
$$
g\left(h_{1}\right)=0.380610 \quad g\left(h_{1} / 2\right)=0.371035
$$
The truncation error in the central difference approximation is $E(h)=\mathcal{O}\left(h^{2}\right)=c_{1} h^{2}+$ $c_{2} h^{4}+c_{3} h^{6}+\cdots$. Therefore, we can eliminate the first (dominant) error term if we substitute $p=2$ and $h_{1}=0.64$ in Eq. (5.9b). The result is
$$
G=\frac{2^{2} g(0.32)-g(0.64)}{2^{2}-1}=\frac{4(0.371035)-0.380610}{3}=0.367843
$$
which is an approximation of $\left(e^{-x}\right)^{\prime \prime}$ with the error $\mathcal{O}\left(h^{4}\right)$. Note that it is as accurate as the best result obtained with eight-digit computations in Table 5.4.
matlab代写
数学代写|MATLAB代写|INTRODUCTION
数值微分处理以下问题:给定函数是=F(X)并希望在该点获得其衍生物之一X=Xķ. 术语“给定”意味着我们要么有一个计算函数的算法,要么拥有一组离散的数据点(X一世,是一世),一世=1,2,…,n. 在任何一种情况下,我们都可以访问有限数量的(X,是)从中计算导数的数据对。如果您现在怀疑数值微分与插值有关,那么找到导数的一种方法是通过多项式局部逼近该函数,然后对其进行微分。一个同样有效的工具是泰勒级数展开F(X)关于这一点Xķ. 后者的优点是为我们提供了有关近似误差的信息。
数值微分不是一个特别准确的过程。它遭受舍入误差之间的冲突d在和吨这l一世米一世吨和d米一种CH一世n和pr和C一世s一世这n和插值中固有的错误。因此,函数的导数永远不能以与函数本身相同的精度计算。
数学代写|MATLAB代写|FINITE DIFFERENCE APPROXIMATIONS
的导数的有限差分近似的推导F(X)是基于前向和后向泰勒级数展开F(X)关于X, 如
F(X+H)=F(X)+HF′(X)+H22!F′′(X)+H33!F′′′(X)+H44!F(4)(X)+⋯F(X−H)=F(X)−HF′(X)+H22!F′′(X)−H33!F′′′(X)+H44!F(4)(X)−⋯ F(X+2H)=F(X)+2HF′(X)+(2H)22!F′′(X)+(2H)33!F′′′(X)+(2H)44!F(4)(X)+⋯ F(X−2H)=F(X)−2HF′(X)+(2H)22!F′′(X)−(2H)33!F′′′(X)+(2H)44!F(4)(X)−⋯
我们还记录了该系列的和与差:
F(X+H)+F(X−H)=2F(X)+H2F′′(X)+H412F(4)(X)+⋯ F(X+H)−F(X−H)=2HF′(X)+H33F′′′(X)+⋯ F(X+2H)+F(X−2H)=2F(X)+4H2F′′(X)+4H43F(4)(X)+⋯ F(X+2H)−F(X−2H)=4HF′(X)+8H33F′′′(X)+⋯
请注意,和仅包含偶数导数,而差异仅保留奇数导数。方程一种-H可以看作是可以求解各种导数的联立方程F(X). 涉及的方程数和每个方程中保留的项数取决于导数的阶数和所需的准确度。
数学代写|MATLAB代写|RICHARDSON EXTRAPOLATION
理查森外推法是一种提高某些数值程序准确性的简单方法,包括有限差分逼近在和在一世ll一种ls这在s和一世吨l一种吨和r一世nn在米和r一世C一种l一世n吨和Gr一种吨一世这n.
假设我们有一种计算某个数量的近似方法G. 此外,假设结果取决于参数H. 表示近似值G(H), 我们有G=G(H)+和(H), 在哪里和(H)表示误差。理查森外推可以消除错误,前提是它具有以下形式和(H)=CHp,C和p是常数。我们从计算开始G(H)有一些价值H, 说H=H1. 在这种情况下,我们有
G=G(H1)+CH1p
然后我们重复计算H=H2, 以便
G=G(H2)+CH2p
消除C并解决G,我们从方程式获得。一世和j
G=(H1/H2)pG(H2)−G(H1)(H1/H2)p−1
这是理查森外推公式。常用的做法是使用H2=H1/2,在这种情况下,方程式。5.9一种变成
G=2pG(H1/2)−G(H1)2p−1
让我们通过将 Richardson 外推法应用于有限差分近似来说明(和−X)′′在X=1. 我们以六位数的精度工作,并利用表 5.4 中的结果。由于外推仅适用于截断误差,我们必须限制H到产生可忽略不计的舍入的值。选择H1=0.64并让G(H)近似于F′′(1)获得H,我们从表中得到5.4
G(H1)=0.380610G(H1/2)=0.371035
中心差分近似中的截断误差为和(H)=这(H2)=C1H2+ C2H4+C3H6+⋯. 因此,我们可以消除第一个d这米一世n一种n吨如果我们替换,则错误项p=2和H1=0.64在等式。5.9b. 结果是
G=22G(0.32)−G(0.64)22−1=4(0.371035)−0.3806103=0.367843
这是一个近似值(和−X)′′有错误这(H4). 请注意,它与表 5.4 中使用八位计算获得的最佳结果一样准确。

数学代写|matlab代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。