如果你也在 怎样代写matlab这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。matlab是由MathWorks公司开发的一种专有的多范式编程语言和数字计算环境。MATLAB允许进行矩阵操作、绘制函数和数据、实现算法、创建用户界面以及与用其他语言编写的程序对接。
matlab尽管MATLAB主要用于数值计算,但一个可选的工具箱使用MuPAD符号引擎,允许访问符号计算能力。一个额外的软件包,Simulink,为动态和嵌入式系统增加了图形化的多域仿真和基于模型的设计。截至2020年,MATLAB在全球拥有超过400万用户。他们来自工程、科学和经济的各种背景。
my-assignmentexpert™ matlab作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的matlab作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此matlab作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的matlab代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种matlab相关的作业也就用不着 说。
我们提供的matlab及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|matlab代写|Introduction
The general form of a first-order differential equation is
$$
y^{\prime}=f(x, y)
$$
where $y^{\prime}=d y / d x$ and $f(x, y)$ is a given function. The solution of this equation contains an arbitrary constant (the constant of integration). To find this constant, we must know a point on the solution curve; that is, $y$ must be specified at some value of $x$, say at $x=a$. We write this auxiliary condition as
$$
y(a)=\alpha
$$
An ordinary differential equation of order $n$
$$
y^{(n)}=f\left(x, y, y^{\prime}, \ldots, y^{(n-1)}\right)
$$
can always be transformed into $n$ first-order equations. Using the notation
$$
y_{1}=y \quad y_{2}=y^{\prime} \quad y_{3}=y^{\prime \prime} \quad \ldots \quad y_{n}=y^{(n-1)}
$$
the equivalent first-order equations are
$$
y_{1}^{\prime}=y_{2} \quad y_{2}^{\prime}=y_{3} \quad y_{3}^{\prime}=y_{4} \quad \ldots \quad y_{n}^{\prime}=f\left(x, y_{1}, y_{2}, \ldots, y_{n}\right)
$$
The solution now requires the knowledge $n$ auxiliary conditions. If these conditions are specified at the same value of $x$, the problem is said to be an initial value problem. Then the auxiliary conditions, called initial conditions, have the form
$$
y_{1}(a)=\alpha_{1} \quad y_{2}(a)=\alpha_{2} \quad y_{3}(a)=\alpha_{3} \quad \ldots \quad y_{n}(a)=\alpha_{n}
$$
数学代写|matlab代写|Taylor Series Method
The Taylor series method is conceptually simple and capable of high accuracy. Its basis is the truncated Taylor series for $\mathrm{y}$ about $x$ :
$$
\mathbf{y}(x+h) \approx \mathbf{y}(x)+\mathbf{y}^{\prime}(x) h+\frac{1}{2 !} \mathbf{y}^{\prime \prime}(x) h^{2}+\frac{1}{3 !} \mathbf{y}^{\prime \prime \prime}(x) h^{3}+\cdots+\frac{1}{n !} \mathbf{y}^{(m)}(x) h^{m}
$$
Because Eq. (7.6) predicts $\mathrm{y}$ at $x+h$ from the information available at $x$, it is also a formula for numerical integration. The last term kept in the series determines the order of integration. For the series in Eq. (7.6) the integration order is $m$.
The truncation error, due to the terms omitted from the series, is
$$
\mathbf{E}=\frac{1}{(m+1) !} \mathbf{y}^{(m+1)}(\xi) h^{m+1}, \quad x<\xi<x+h
$$
Using the finite difference approximation
$$
\mathbf{y}^{(m+1)}(\xi) \approx \frac{\mathbf{y}^{(m)}(x+h)-\mathbf{y}^{(m)}(x)}{h}
$$
we obtain the more usable form
$$
\mathbf{E} \approx \frac{h^{m}}{(m+1) !}\left[\mathbf{y}^{(m)}(x+h)-\mathbf{y}^{(m)}(x)\right]
$$
which could be incorporated in the algorithm to monitor the error in each integration step.
数学代写|MATLAB代写|Runge–Kutta Methods
The aim of Runge-Kutta methods is to eliminate the need for repeated differentiation of the differential equations. Since no such differentiation is involved in the first-order Taylor series integration formula
$$
\mathbf{y}(x+h)=\mathbf{y}(x)+\mathbf{y}^{\prime}(x) h=\mathbf{y}(x)+\mathbf{F}(x, \mathbf{y}) h
$$
it can be considered as the first-order Runge-Kutta method; it is also called Euler’s method. Due to excessive truncation error, this method is rarely used in practice.
Let us now take a look at the graphical interpretation of Euler’s formula. For the sake of simplicity, we assume that there is a single dependent variable $y$, so that the differential equation is $y^{\prime}=f(x, y)$. The change in the solution $y$ between $x$ and $x+h$ is
$$
y(x+h)-y(h)=\int_{x}^{x+h} y^{\prime} d x=\int_{x}^{x+h} f(x, y) d x
$$
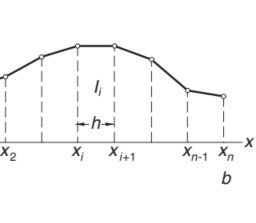
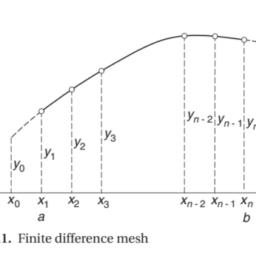
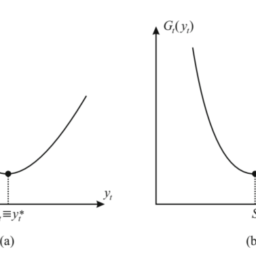
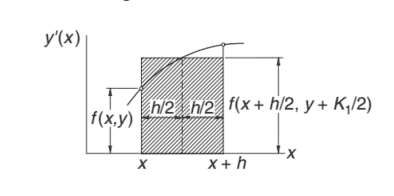
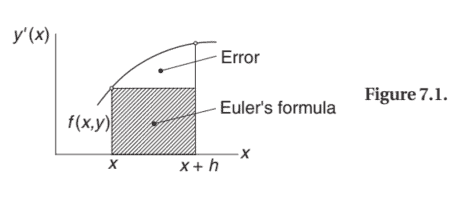
which is the area of the panel under the $y^{\prime}(x)$ plot, shown in Fig. 7.1. Euler’s formula approximates this area by the area of the cross-hatched rectangle. The area between the rectangle and the plot represents the truncation error. Clearly, the truncation error is proportional to the slope of the plot; that is, proportional to $y^{\prime \prime}(x)$.
matlab代写
数学代写|MATLAB代写|INTRODUCTION
一阶微分方程的一般形式是
是′=F(X,是)
在哪里是′=d是/dX和F(X,是)是给定的函数。这个方程的解包含一个任意常数吨H和C这ns吨一种n吨这F一世n吨和Gr一种吨一世这n. 要找到这个常数,我们必须知道解曲线上的一个点;那是,是必须指定为某个值X,说在X=一种. 我们把这个辅助条件写成
是(一种)=一种
常微分方程n
是(n)=F(X,是,是′,…,是(n−1))
总是可以转化为n一阶方程。使用符号
是1=是是2=是′是3=是′′…是n=是(n−1)
等效的一阶方程是
是1′=是2是2′=是3是3′=是4…是n′=F(X,是1,是2,…,是n)
解决方案现在需要知识n辅助条件。如果这些条件被指定为相同的值X,该问题称为初值问题。然后辅助条件,称为初始条件,具有以下形式
是1(一种)=一种1是2(一种)=一种2是3(一种)=一种3…是n(一种)=一种n
数学代写|MATLAB代写|TAYLOR SERIES METHOD
泰勒级数方法在概念上很简单并且具有很高的准确性。它的基础是截断的泰勒级数是关于X :
是(X+H)≈是(X)+是′(X)H+12!是′′(X)H2+13!是′′′(X)H3+⋯+1n!是(米)(X)H米
因为方程。7.6预测是在X+H从可用的信息X,它也是数值积分的公式。系列中保留的最后一项决定了积分的顺序。对于方程式中的系列。7.6整合顺序是米.
由于系列中省略的项,截断误差为
和=1(米+1)!是(米+1)(X)H米+1,X<X<X+H
使用有限差分近似
是(米+1)(X)≈是(米)(X+H)−是(米)(X)H
我们得到更有用的形式
和≈H米(米+1)![是(米)(X+H)−是(米)(X)]
可以将其合并到算法中以监视每个集成步骤中的错误。
数学代写|MATLAB代写|RUNGE–KUTTA METHODS
Runge-Kutta 方法的目的是消除对微分方程重复微分的需要。由于一阶泰勒级数积分公式中不涉及这种微分
是(X+H)=是(X)+是′(X)H=是(X)+F(X,是)H
可以认为是一阶龙格-库塔法;它也被称为欧拉方法。由于截断误差过大,这种方法在实际中很少使用。
现在让我们看一下欧拉公式的图形解释。为了简单起见,我们假设有一个因变量是, 使得微分方程为是′=F(X,是). 解决方案的变化是之间X和X+H是
是(X+H)−是(H)=∫XX+H是′dX=∫XX+HF(X,是)dX
这是面板下方的区域是′(X)图,如图 7.1 所示。欧拉公式通过交叉影线矩形的面积来近似该面积。矩形和绘图之间的区域表示截断误差。显然,截断误差与图的斜率成正比;也就是说,与是′′(X).

数学代写|matlab代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。