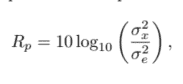如果你也在 怎样代写数字信号处理digital signal process这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。数字信号处理digital signal process是指使用数字处理,如通过计算机或更专业的数字信号处理器,来进行各种信号处理操作。以这种方式处理的数字信号是一连串的数字,代表时间、空间或频率等领域中连续变量的样本。在数字电子学中,数字信号被表示为脉冲序列,它通常由晶体管的开关产生。
数字信号处理digital signal process和模拟信号处理是信号处理的子领域。DSP的应用包括音频和语音处理、声纳、雷达和其他传感器阵列处理、频谱密度估计、统计信号处理、数字图像处理、数据压缩、视频编码、音频编码、图像压缩、电信的信号处理、控制系统、生物医学工程和地震学等。
my-assignmentexpert™ 数字信号处理digital signal process作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的数字信号处理digital signal process作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此数字信号处理digital signal process作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在信息Information作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数字信号处理digital signal process代写服务。我们的专家在信息Information代写方面经验极为丰富,各种数字信号处理digital signal process相关的作业也就用不着 说。
我们提供的数字信号处理digital signal process及其相关学科的代写,服务范围广, 其中包括但不限于:
调和函数 harmonic function
椭圆方程 elliptic equation
抛物方程 Parabolic equation
双曲方程 Hyperbolic equation
非线性方法 nonlinear method
变分法 Calculus of Variations
几何分析 geometric analysis
偏微分方程数值解 Numerical solution of partial differential equations
信号代写|数字信号处理作业代写digital signal process代考|Fixed-point Number Representation
In general, an arbitrary real number $x$ can be approximated by a finite summation
$$
x_{Q}=\sum_{i=0}^{w-1} b_{i} 2^{i}
$$
where the possible values for $b_{i}$ are 0 and 1 .
The fixed-point number representation with a finite number $w$ of binary places leads to four different interpretations of the number range (see Table $2.1$ and Fig. 2.35).
The signed fractional representation (2’s complement) is the usual format for digital audio signals and for algorithms in fixed-point arithmetic. For address and modulo operation, the unsigned integer is used. Owing to finite word-length $w$, overflow occurs as shown in Fig. 2.36. These curves have to be taken into consideration while carrying out operations, especially additions in 2’s complement arithmetic.
信号代写|数字信号处理作业代写digital signal process代考|Floating-point Number Representation
The representation of a floating-point number is given by
$$
x_{Q}=M_{G} 2^{E_{G}}
$$
with
$0.5 \leq M_{G}<1$,
where $M_{G}$ denotes the normalized mantissa and $E_{G}$ the exponent. The normalized standard format (IEEE) is shown in Fig. $2.40$ and special cases are given in Table 2.3. The mantissa $M$ is implemented with a word-length of $w_{M}$ bits and is in fixed-point number representation. The exponent $E$ is implemented with a word-length of $w_{E}$ bits and is an integer in the range from $-2^{w_{E}-1}+2$ to $2^{w_{E}-1}-1$. For an exponent word-length of $w_{E}=8$ bits, its range of values lies between $-126$ and $+127$. The range of values of the mantissa lies between $0.5$ and 1 . This is referred to as the normalized mantissa and is responsible for the unique representation of a number. For a fixed-point number in the range between $0.5$ and 1, it follows that the exponent of the floating-point number representation is $E=0$. To represent a fixed-point number in the range between $0.25$ and $0.5$ in floatingpoint form, the range of values of the normalized mantissa $M$ lies between $0.5$ and 1 , and for the exponent it follows that $E=-1$. As an example, for a fixed-point number $0.75$ the floating-point number $0.75 \cdot 2^{0}$ results. The fixed-point number $0.375$ is not represented as the floating-point number $0.375 \cdot 2^{0}$. With the normalized mantissa, the floating-point number is expressed as $0.75 \cdot 2^{-1}$. Owing to normalization, the ambiguity of floating-point number representation is avoided. Numbers greater than 1 can be represented. For example, $1.5$ becomes $0.75 \cdot 2^{1}$ in floating-point number representation.
信号代写|数字信号处理作业代写digital signal process代考|Effects on Format Conversion and Algorithms
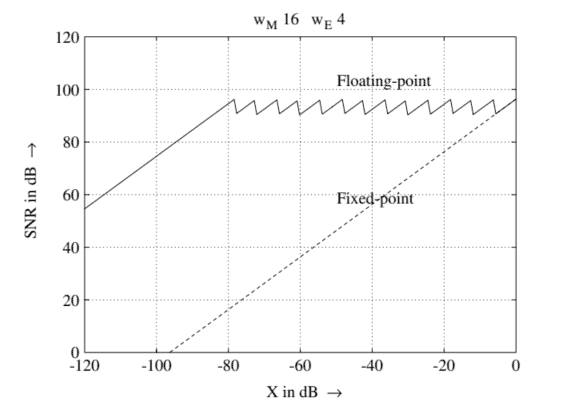
First, a comparison of signal-to-noise ratios is made for the fixed-point and floatingpoint number representation. Figure $2.43$ shows the signal-to-noise ratio as a function of input level for both number representations. The fixed-point word-length is $w=16$ bits. The word-length of the mantissa in floating-point representation is also $w_{M}=16$ bits, whereas that of the exponent is $w_{E}=4$ bits. The signal-to-noise ratio for floating-point representation shows that it is independent of input level and varies as a sawtooth curve in a $6 \mathrm{~dB}$ grid. If the input level is so low that a normalization of the mantissa due to finite number representation is not possible, then the signal-to-noise ratio is comparable to fixed-point representation. While using the full range, both fixed-point and floating-point result in the same signal-to-noise ratio. It can be observed that the signal-to-noise ratio for fixed-point representation depends on the input level. This signal-to-noise ratio in the digital domain is an exact image of the level-dependent signal-to-noise ratio of an analog signal in the analog domain. A floating-point representation cannot improve this signal-tonoise ratio. Rather, the floating-point curve is vertically shifted downwards to the value of signal-to-noise ratio of an analog signal.
数字信号处理代写
信号代写|数字信号处理作业代写DIGITAL SIGNAL PROCESS代考|FIXED-POINT NUMBER REPRESENTATION
通常,任意实数X可以用有限求和来近似
X问=∑一世=0在−1b一世2一世
其中可能的值为b一世是 0 和 1 。
具有有限数的定点数表示在二进制位置导致对数字范围的四种不同解释s和和吨一种bl和$2.1$一种ndF一世G.2.35.
有符号小数表示2′sC这米pl和米和n吨是数字音频信号和定点算术算法的常用格式。对于地址和模运算,使用无符号整数。由于字长有限在,溢出发生如图 2.36 所示。在执行运算时必须考虑这些曲线,尤其是 2 的补码运算中的加法。
信号代写|数字信号处理作业代写DIGITAL SIGNAL PROCESS代考|FLOATING-POINT NUMBER REPRESENTATION
浮点数的表示由下式给出
X问=米G2和G
和
0.5≤米G<1,
其中米G表示归一化尾数和和G指数。标准化的标准格式一世和和和如图所示。2.40特殊情况见表 2.3。尾数米用字长实现在米位并且是定点数表示。指数和用字长实现在和位,并且是范围内的整数−2在和−1+2到2在和−1−1. 对于指数字长在和=8位,其取值范围介于−126和+127. 尾数的取值范围介于0.5和 1。这被称为归一化尾数,负责数字的唯一表示。对于范围内的定点数0.5和 1,因此浮点数表示的指数是和=0. 表示范围内的定点数0.25和0.5以浮点形式,归一化尾数的值范围米介于0.5和 1 ,对于指数,它遵循和=−1. 例如,对于定点数0.75浮点数0.75⋅20结果。定点数0.375不表示为浮点数0.375⋅20. 使用归一化尾数,浮点数表示为0.75⋅2−1. 由于归一化,避免了浮点数表示的歧义。可以表示大于 1 的数字。例如,1.5变成0.75⋅21在浮点数表示中。
信号代写|数字信号处理作业代写DIGITAL SIGNAL PROCESS代考|EFFECTS ON FORMAT CONVERSION AND ALGORITHMS
首先,对定点数和浮点数表示的信噪比进行比较。数字2.43显示了两种数字表示的信噪比作为输入电平的函数。定点字长为在=16位。浮点表示中尾数的字长也是在米=16位,而指数的位是在和=4位。浮点表示的信噪比表明它与输入电平无关,并且在6 d乙网格。如果输入电平太低以至于由于有限数表示而无法对尾数进行归一化,则信噪比与定点表示相当。在使用全范围时,定点和浮点都会产生相同的信噪比。可以观察到,定点表示的信噪比取决于输入电平。数字域中的这种信噪比是模拟域中模拟信号的电平相关信噪比的精确图像。浮点表示不能改善这种信噪比。相反,浮点曲线垂直向下移动到模拟信号的信噪比值。

信号代写|数字信号处理作业代写digital signal process代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。