如果你也在 怎样代写信号和系统signals and systems这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。信号和系统signals and systems信号是对一个参数如何随另一个参数变化的描述。例如,电子电路中电压随时间变化,或图像中亮度随距离变化。一个系统是任何对输入信号产生输出信号的过程。
信号和系统signals and systems是对模拟和数字信号处理的介绍,这一主题构成了许多不同领域的工程系统的一个组成部分,包括地震数据处理、通信、语音处理、图像处理、国防电子、消费电子和消费产品。
my-assignmentexpert™ 信号和系统signals and systems作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的信号和系统signals and systems作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此信号和系统signals and systems作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在信息Information作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的信号和系统signals and systems代写服务。我们的专家在信息Information代写方面经验极为丰富,各种信号和系统signals and systems相关的作业也就用不着 说。
我们提供的信号和系统signals and systems及其相关学科的代写,服务范围广, 其中包括但不限于:
调和函数 harmonic function
椭圆方程 elliptic equation
抛物方程 Parabolic equation
双曲方程 Hyperbolic equation
非线性方法 nonlinear method
变分法 Calculus of Variations
几何分析 geometric analysis
偏微分方程数值解 Numerical solution of partial differential equations
信号代写|信号和系统作业代写signals and systems代考|Orthogonal vector space
From the theory of vector space, we know that an arbitrary $M$-dimensional vector can be represented in terms of its $M$ orthogonal coordinates. For example, a two-dimensional (2D) vector $\vec{V}$ with coordinates $\left(v_{i}, v_{j}\right)$ can be expressed as follows:
$$
\vec{V}=v_{i} \vec{i}+v_{j} \vec{j}
$$
where $\vec{i}$ and $\vec{j}$ are the two basis vectors, respectively, along the $x$-and $y$-axis. A graphical representation for the $2 \mathrm{D}$ vector is illustrated in Fig. 4.1(a). The two basis vectors $\vec{i}$ and $\vec{j}$ have unit magnitudes and are perpendicular to each other, as described by the following two properties:
orthogonality property $\quad \vec{i} \cdot \vec{j}=|\vec{i}||\vec{j}| \cos 90^{\circ}=0$;
unit magnitude property $\left{\begin{array}{l}\vec{i} \cdot \vec{i}=|\vec{i}||\vec{i}| \cos 0^{\circ}=1 \ \vec{j} \cdot \vec{j}=|\vec{j}||\vec{j}| \cos 0^{\circ}=1\end{array}\right.$
信号代写|信号和系统作业代写signals and systems代考|Orthogonal signal space
Two non-zero signals $p(t)$ and $q(t)$ are said to be orthogonal over interval $t=\left[t_{1}, t_{2}\right]$ if
$$
\int_{t_{1}}^{t_{2}} p(t) q^{}(t) \mathrm{d} t=\int_{t_{1}}^{t_{2}} p^{}(t) q(t) \mathrm{d} t=0,
$$
where the superscript $$ denotes the complex conjugation operator: In addition to Eq. (4.8), if both signals $p(t)$ and $q(t)$ also satisfy the unit magnitude property: $$ \int_{t_{1}}^{t_{2}} p(t) p^{}(t) \mathrm{d} t=\int_{t_{1}}^{t_{2}} q(t) q^{*}(t) \mathrm{d} t=1,
$$
they are said to be orthonormal to each other over the interval $t=\left[t_{1}, t_{2}\right]$.
Show that
(i) functions $\cos (2 \pi t)$ and $\cos (3 \pi t)$ are orthogonal over interval $t=[0,1]$;
(ii) functions $\exp (\mathrm{j} 2 t)$ and $\exp (\mathrm{j} 4 t)$ are orthogonal over interval $t=[0, \pi]$;
(iii) functions $\cos (t)$ and $t$ are orthogonal over interval $t=[-1,1]$.
信号代写|信号和系统作业代写SIGNALS AND SYSTEMS代考|Fourier basis functions
It was observed that the output response of an RLC circuit to a sinusoidal function was another sinusoidal function of the same frequency. The changes observed in the input sinusoidal function were only in its amplitude and phase. Below we illustrate that the property holds true for any LTIC system. Further, we extend the property to complex exponential signals proving that the output response of an LTIC system to a complex exponential function is another complex exponential with the same frequency, except for possible changes in its amplitude and phase.
Theorem 4.1 If a complex exponential function is applied to an LTIC system with a real-valued impulse response function, the output response of the system is identical to the complex exponential function except for changes in amplitude and phase. In other words,
$$
k_{1} \mathrm{e}^{\mathrm{j} \omega_{1} t} \rightarrow A_{1} k_{1} \mathrm{e}^{\mathrm{j}\left(\omega_{1} t+\phi_{1}\right)},
$$
where $A_{1}$ and $\phi_{1}$ are constants.
信号和系统代写
信号代写|信号和系统作业代写SIGNALS AND SYSTEMS代考|ORTHOGONAL VECTOR SPACE
根据向量空间理论,我们知道任意米维向量可以表示为米正交坐标。例如,一个二维2D向量在→带坐标(在一世,在j)可以表示如下:
在→=在一世一世→+在jj→
在哪里一世→和j→是两个基向量,分别沿X-和是-轴。的图形表示2D矢量如图 4.1 所示一种. 两个基向量一世→和j→具有单位大小并且相互垂直,如以下两个属性所述:
正交性一世→⋅j→=|一世→||j→|因90∘=0;
单位量级属性$\left{\begin{array}{l}\vec{i} \cdot \vec{i}=|\vec{i}||\vec{i}| \cos 0^{\circ}=1 \ \vec{j} \cdot \vec{j}=|\vec{j}||\vec{j}| \cos 0^{\circ}=1\end{array}\right.$
信号代写|信号和系统作业代写SIGNALS AND SYSTEMS代考|ORTHOGONAL SIGNAL SPACE
两个非零信号p(吨)和q(吨)被称为在区间上正交$t=\left[t_{1}, t_{2}\right]$ if
$$
\int_{t_{1}}^{t_{2}} p(t) q^{}(t) \mathrm{d} t=\int_{t_{1}}^{t_{2}} p^{}(t) q(t) \mathrm{d} t=0,
$$
where the superscript $$ denotes the complex conjugation operator: In addition to Eq. (4.8), if both signals $p(t)$ and $q(t)$ also satisfy the unit magnitude property: $$ \int_{t_{1}}^{t_{2}} p(t) p^{}(t) \mathrm{d} t=\int_{t_{1}}^{t_{2}} q(t) q^{*}(t) \mathrm{d} t=1,
$$
它们在区间内相互正交吨=[吨1,吨2].
显示
(i) functions $\cos (2 \pi t)$ and $\cos (3 \pi t)$ are orthogonal over interval $t=[0,1]$;
(ii) functions $\exp (\mathrm{j} 2 t)$ and $\exp (\mathrm{j} 4 t)$ are orthogonal over interval $t=[0, \pi]$;
(iii) functions $\cos (t)$ and $t$ are orthogonal over interval $t=[-1,1]$.
信号代写|信号和系统作业代写SIGNALS AND SYSTEMS代考|FOURIER BASIS FUNCTIONS
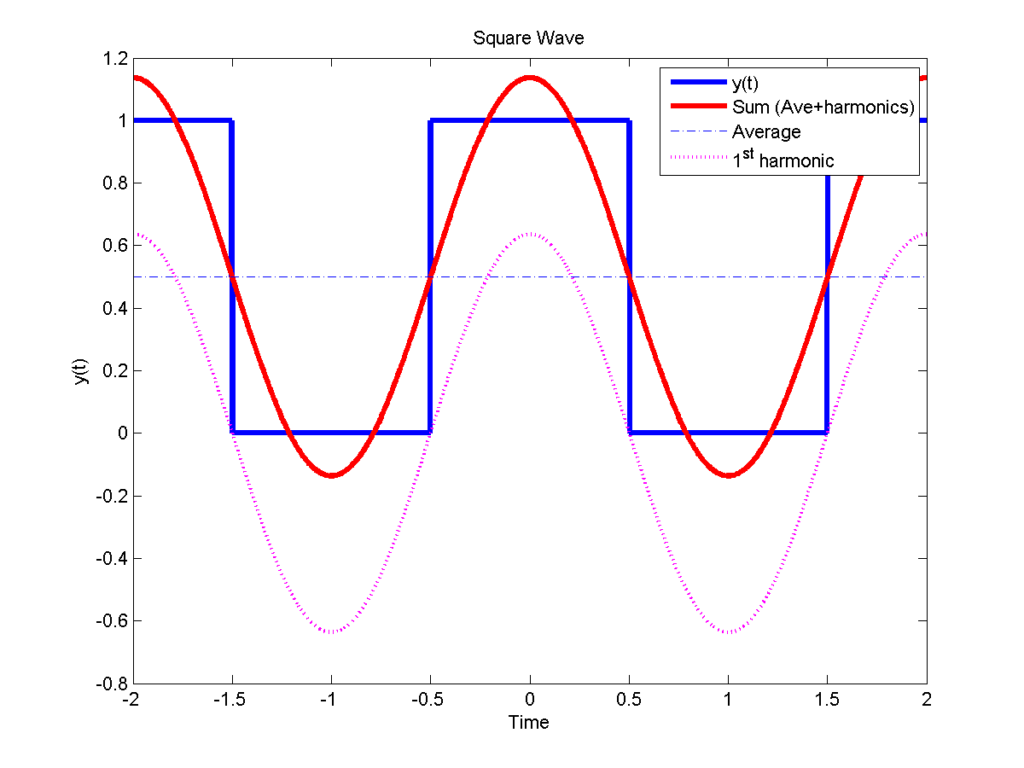
据观察,RLC 电路对正弦函数的输出响应是另一个相同频率的正弦函数。在输入正弦函数中观察到的变化仅在其幅度和相位上。下面我们说明该属性适用于任何 LTIC 系统。此外,我们将该属性扩展到复指数信号,证明 LTIC 系统对复指数函数的输出响应是另一个具有相同频率的复指数,除了其幅度和相位可能发生变化。
定理 4.1 如果将复指数函数应用于具有实值脉冲响应函数的 LTIC 系统,则系统的输出响应与复指数函数相同,只是幅度和相位发生变化。换句话说,
ķ1和jω1吨→一种1ķ1和j(ω1吨+φ1),
在哪里一种1和φ1是常数。

信号代写|信号和系统作业代写signals and systems代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。