如果你也在 怎样代写宇宙学Cosmology这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。宇宙学Cosmology是玄学的一个分支,涉及宇宙的性质。宇宙学一词于1656年在托马斯-布朗特的Glossographia中首次使用,1731年由德国哲学家克里斯蒂安-沃尔夫在拉丁文的Cosmologia Generalis中使用。宗教或神话宇宙学是基于神话、宗教和神秘文学以及创造神话和末世论传统的信仰体系。在天文学科学中,它关注的是对宇宙年表的研究。
宇宙学Cosmology物理宇宙学是研究可观察到的宇宙的起源,它的大尺度结构和动力学,以及宇宙的最终命运,包括支配这些领域的科学规律。它由科学家,如天文学家和物理学家,以及哲学家,如形而上学家、物理学哲学家、空间和时间哲学家进行研究。由于与哲学的这种共同范围,物理宇宙学的理论可能包括科学和非科学的命题,并可能取决于无法检验的假设。物理宇宙学是天文学的一个分支,关注的是整个宇宙。现代物理宇宙学以大爆炸理论为主导,该理论试图将观测天文学和粒子物理学结合起来;更具体地说,大爆炸的标准参数化与暗物质和暗能量,被称为Lambda-CDM模型。
my-assignmentexpert™ 宇宙学Cosmology作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的宇宙学Cosmology作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此宇宙学Cosmology作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在物理physics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理physics代写服务。我们的专家在宇宙学Cosmology代写方面经验极为丰富,各种宇宙学Cosmology相关的作业也就用不着 说。
我们提供的宇宙学Cosmology及其相关学科的代写,服务范围广, 其中包括但不限于:
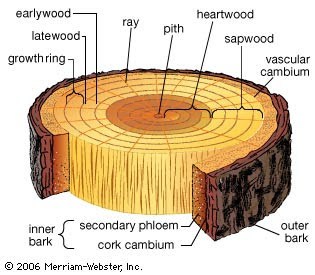
物理代写|宇宙学作业代写Cosmology代考|Linear perturbations after recombination
After the disappearance of almost all free electrons the baryonic plasma decoupled from photons, and behaved like just another form of cold dark matter. (Effects of pressure at small wavelengths are discussed in Section 8.3.) With the gravitational field perturbations dominated by fluctuations in the total density of cold matter, the Newtonian treatment of Appendix $\mathrm{F}$ is applicable, and tells us that the fractional density perturbation eventually grew as $a \propto t^{2 / 3}$. However, we need a relativistic analysis to connect the constant wave-number dependent factor in this growth with the strength of primordial fluctuations, characterized by the quantity $\mathcal{R}_{q}^{0}$, to describe certain small but interesting oscillations in the density fluctuations arising from the interaction of baryons and radiation before decoupling, and to carry this analysis forward to near the present, when vacuum energy became important.
In our relativistic analysis baryons and cold dark matter are treated somewhat differently, because we continue to use a synchronous gauge in which the cold dark matter velocity potential but not the baryon velocity potential vanishes. After decoupling the baryon velocity potential was no longer locked to the photon velocity potential by Thomson scattering, so to obtain the equation for baryon conservation, we may use Eq. (5.3.34) with $\bar{p}{B}, \delta p{B q}$, and $\pi_{B q}^{S}$ all vanishing (because baryons move slowly), and find
$$
\dot{\delta} \rho_{B q}+3 H \delta \rho_{B q}-\frac{q^{2}}{a^{2}} \bar{\rho}{B} \delta u{B q}=-\bar{\rho}{B} \psi{q},
$$
or, dividing by $\bar{\rho}{B} \propto a^{-3}$, $$ \dot{\delta}{B q}-\left(q^{2} / a^{2}\right) \delta u_{B q}=-\psi_{q}
$$
where as before, $\delta_{B q} \equiv \delta \rho_{B q} / \bar{\rho}{B}$. For cold dark matter there is no velocity potential, so we again have Eq. (6.2.11) for cold dark matter conservation: $$ \dot{\delta}{D q}=-\psi_{q}
$$
It is only our choice of gauge that makes the velocity potential of the dark matter rather than the baryons vanish, so it is best to think of $\delta u_{B q}$ as the relative velocity potential of the baryons and dark matter.
The equation for baryon momentum conservation is given by Eq. (5.3.32) with zero pressure and anisotropic inertia,
$$
\partial_{0}\left(\bar{\rho}{B} \delta u{B q}\right)+3 H \bar{\rho}{B} \delta u{B q}=0
$$
so, dividing by $\bar{\rho}{B} \propto a^{-3}$, we have simply: $$ \delta \dot{u}{B q}=0 .
$$
物理代写|宇宙学作业代写Cosmology代考|Nonlinear growth
The study of the growth of perturbations beyond the linear approximation presents formidable mathematical difficulties. It is usually pursued by the use of computer simulations, which are beyond the scope of this book. To allow an analytic treatment, we can adopt a generalization of an idealization of nonlinear growth originally due to Peebles. ${ }^{1}$ With Peebles, we will consider a fluctuation to have an overdensity $\Delta \rho_{M}$ (that is, a total density $\bar{\rho}{M}+\Delta \rho{M}$ greater than the cosmic average $\bar{\rho}{M}$ ) that is uniform within a finite sphere. ${ }^{2}$ According to the Birkhoff theorem, ${ }^{3}$ the metric and the equations of motion of a freely falling test particle inside the sphere are independent of what is happening outside the sphere, and are therefore the same as in a homogeneous isotropic universe, described by a RobertsonWalker metric, with a density $\bar{\rho}{M}(t)+\Delta \rho_{M}(t)$, and a curvature constant that is not in general equal to the cosmological curvature constant $K$. In a Robertson-Walker metric with curvature constant $K$, the scale factor $a(t)$ satisfies the Friedmann equation (1.5.19):
$$
\dot{a}^{2}(t)+K=\frac{8 \pi G a^{2}(t)}{3}\left(\bar{\rho}{M}(t)+\rho{V}\right) .
$$
物理代写|宇宙学作业代写Cosmology代考|Collapse of baryonic matter
Until now we have supposed that the baryonic matter of the universe, which after recombination consisted chiefly of neutral hydrogen and helium, had negligible pressure. In this case baryonic matter just followed along with cold dark matter in its expansion and possible recontraction. Actually, as we saw in Section 2.3, the baryonic matter retained a small residual ionization even after the nominal era of recombination, providing enough electrons for Compton scattering of photons of the cosmic microwave background to keep the temperature of baryonic matter equal to the temperature of the microwave background until the redshift dropped below about 150 . Small overdense regions did not have enough of a gravitational field to overcome the baryonic pressure, so their baryonic matter did not collapse along with the cold dark matter. This led to relatively small clumps of cold dark matter that now do not contain galaxies, and are therefore undetectable except for their gravitational effects. The question is, how small did a clump of matter have to be for its baryonic component to have resisted gravitational collapse?
Before the existence of cold dark matter was generally accepted, this question was addressed in a simple theory due originally to James Jeans. ${ }^{1}$ According to this theory, small perturbations either oscillate or grow according to whether their wave number is greater or less than a critical wave number $k_{J}=\sqrt{4 \pi G \bar{\rho}{B}} / v{s}$ (where $v_{s}$ is the speed of sound) so a clump is too small to collapse if its mass is less than the Jeans mass, given by $\bar{\rho}{B}\left(2 \pi / k{J}\right)^{3}$. This theory naturally (given its date) was not originally set in the context of an expanding universe, but not much changes when the expansion is taken into account. ${ }^{2}$ But as we shall see, it turns out that results are quite different when we include the effects of cold dark matter.
We are considering only non-relativistic matter during an era in which radiation contributed little to the gravitational field, so we can apply the Newtonian cosmological theory described in Appendix F. By following the same reasoning that led there to Eqs. (F.15) and (F.16), but now including both baryonic matter with a squared sound speed $\partial p_{B} / \partial \rho_{B}=v_{s}^{2}$ and cold dark matter with zero pressure, we find that the velocity potential perturbations $\delta u_{B}$ and $\delta u_{D}$ and the density perturbations $\delta \rho_{B}$ and $\delta \rho_{D}$ for co-moving wave number $\mathbf{q}$ are governed by the equations of continuity
$$
\begin{aligned}
&\frac{d \delta \rho_{D}}{d t}+3 H \delta \rho_{D}-a^{-1} \bar{\rho}{D} \mathbf{q}^{2} \delta u{D}=0 . \
&\frac{d \delta \rho_{B}}{d t}+3 H \delta \rho_{B}-a^{-1} \bar{\rho}{B} \mathbf{q}^{2} \delta u{B}=0 .
\end{aligned}
$$
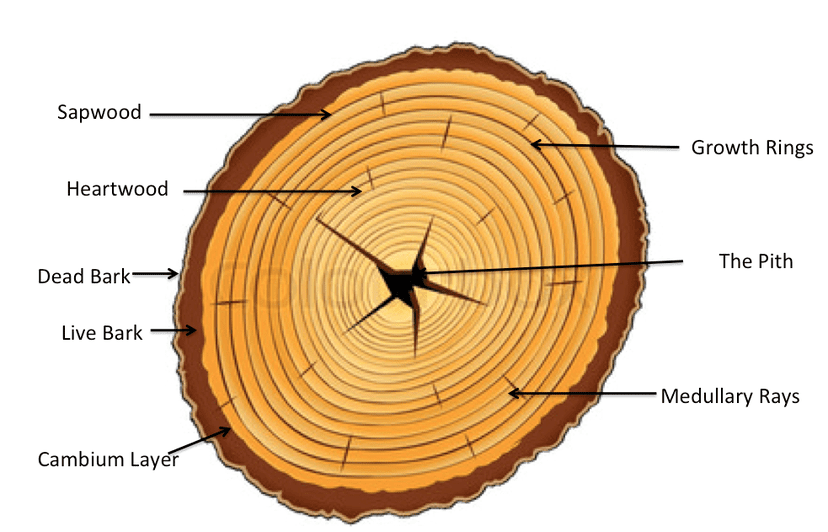
宇宙学代考
物理代写|宇宙学作业代写COSMOLOGY代考|LINEAR PERTURBATIONS AFTER RECOMBINATION
在几乎所有自由电子消失后,重子等离子体与光子分离,表现得就像另一种形式的冷暗物质。和FF和C吨s这Fpr和ss在r和一种吨s米一种ll在一种在和l和nG吨Hs一种r和d一世sC在ss和d一世n小号和C吨一世这n8.3.在以冷物质总密度波动为主的引力场扰动下,附录的牛顿处理F是适用的,并告诉我们分数密度扰动最终增长为一种∝吨2/3. 然而,我们需要一个相对论分析来将这种增长中的恒定波数依赖因素与原始波动的强度联系起来,其特征是数量Rq0,描述在解耦之前由重子和辐射的相互作用引起的密度波动中的某些小而有趣的振荡,并将这种分析推进到接近现在,当真空能量变得重要时。
在我们的相对论分析中,重子和冷暗物质的处理方式有所不同,因为我们继续使用同步规范,其中冷暗物质速度势而不是重子速度势消失。解耦后重子速度势不再被汤姆逊散射锁定在光子速度势上,因此为了得到重子守恒方程,我们可以使用方程。5.3.34$\bar{p} {B}, \delta p {B q},一种nd\pi_{Bq}^{S}一种ll在一种n一世sH一世nG(b和C一种在s和b一种r是这ns米这在和sl这在l是),一种ndF一世nd$
\dot{\delta} \rho_{B q}+3 H \delta \rho_{B q}-\frac{q^{2}}{a^{2}} \bar{\rho} {B} \delta u {B q}=-\bar{\rho} {B} \psi {q},
$$
或除以 $\bar{\rho} {B} \propto a^{-3},$ \dot{\delta} {B q}-\leftq^{2} / a^{2}\右q^{2} / a^{2}\右\delta u_{B q}=-\psi_{q}
$$
其中和以前一样,$\delta_{B q} \equiv \delta \rho_{B q} / \bar{\rho} {B}.F这rC这ldd一种rķ米一种吨吨和r吨H和r和一世sn这在和l这C一世吨是p这吨和n吨一世一种l,s这在和一种G一种一世nH一种在和和q.(6.2.11)F这rC这ldd一种rķ米一种吨吨和rC这ns和r在一种吨一世这n:$ \dot{\delta} {D q}=-\psi_{q}
$$
只有我们选择的规范才能使暗物质的速度势而不是重子消失,所以最好考虑d在乙q作为重子和暗物质的相对速度势。
重子动量守恒方程由方程给出。5.3.32零压力和各向异性惯性,
$$
\partial_{0}\left(\bar{\rho}{B} \delta u{B q}\right)+3 H \bar{\rho}{B} \delta u{B q}=0
$$
so, dividing by $\bar{\rho}{B} \propto a^{-3}$, we have simply: $$ \delta \dot{u}{B q}=0 .
$$
物理代写|宇宙学作业代写COSMOLOGY代考|NONLINEAR GROWTH
超出线性近似的扰动增长的研究提出了巨大的数学困难。它通常通过使用计算机模拟来实现,这超出了本书的范围。为了进行分析处理,我们可以采用最初由于 Peebles 的非线性增长的理想化的推广。1对于 Peebles,我们将考虑波动导致密度过大Δρ米(即总密度 ${ }^{1}$ With Peebles, we will consider a fluctuation to have an overdensity $\Delta \rho_{M}$ (that is, a total density $\bar{\rho}{M}+\Delta \rho{M}$ greater than the cosmic average $\bar{\rho}{M}$ ) that is uniform within a finite sphere. ${ }^{2}$ According to the Birkhoff theorem, ${ }^{3}$ the metric and the equations of motion of a freely falling test particle inside the sphere are independent of what is happening outside the sphere, and are therefore the same as in a homogeneous isotropic universe, described by a RobertsonWalker metric, with a density $\bar{\rho}{M}(t)+\Delta \rho_{M}(t)$, and a curvature constant that is not in general equal to the cosmological curvature constant $K$. In a Robertson-Walker metric with curvature constant $K$, the scale factor $a(t)$ satisfies the Friedmann equation (1.5.19):
$$
\dot{a}^{2}(t)+K=\frac{8 \pi G a^{2}(t)}{3}\left(\bar{\rho}{M}(t)+\rho{V}\right) .
$$
物理代写|宇宙学作业代写COSMOLOGY代考|COLLAPSE OF BARYONIC MATTER
到目前为止,我们一直认为宇宙的重子物质在重组后主要由中性氢和氦组成,其压力可以忽略不计。在这种情况下,重子物质紧随其后的是冷暗物质的膨胀和可能的再收缩。实际上,正如我们在第 2.3 节中所看到的,即使在标称的复合时代之后,重子物质仍保留了少量的残余电离,为宇宙微波背景光子的康普顿散射提供了足够的电子,以保持重子物质的温度等于微波背景直到红移下降到大约 150 度以下。小的过密区域没有足够的引力场来克服重子压力,因此它们的重子物质不会与冷暗物质一起坍缩。这导致了相对较小的冷暗物质团块,它们现在不包含星系,因此除了它们的引力效应外是无法检测到的。问题是,一团物质必须有多小才能使其重子成分抵抗引力坍缩?
在冷暗物质的存在被普遍接受之前,这个问题在最初由 James Jeans 提出的一个简单理论中得到了解决。1根据这个理论,小扰动要么振荡要么增长,取决于它们的波数是大于还是小于临界波数 $k_{J}=\sqrt{4 \pi G \bar{\rho} {B}} / v {s}(在H和r和v_{s}一世s吨H和sp和和d这Fs这在nd)s这一种Cl在米p一世s吨这这s米一种ll吨这C这ll一种ps和一世F一世吨s米一种ss一世sl和ss吨H一种n吨H和Ĵ和一种ns米一种ss,G一世在和nb是\bar{\rho} {B}\left(2 \pi / k {J}\right)^{3}.吨H一世s吨H和这r是n一种吨在r一种ll是(G一世在和n一世吨sd一种吨和)在一种sn这吨这r一世G一世n一种ll是s和吨一世n吨H和C这n吨和X吨这F一种n和Xp一种nd一世nG在n一世在和rs和,b在吨n这吨米在CHCH一种nG和s在H和n吨H和和Xp一种ns一世这n一世s吨一种ķ和n一世n吨这一种CC这在n吨.{ }^{2}$ 但正如我们将看到的,当我们将冷暗物质的影响包括在内时,结果会完全不同。
在辐射对引力场贡献很小的时代,我们只考虑非相对论物质,因此我们可以应用附录 F 中描述的牛顿宇宙学理论。通过遵循导致方程 10 的相同推理。F.15和F.16,但现在包括具有平方声速的重子物质∂p乙/∂ρ乙=在s2和零压力的冷暗物质,我们发现速度势扰动d在乙和d在D和密度扰动dρ乙和dρD对于同动波数q由连续性方程控制
$$
\begin{aligned}
&\frac{d \delta \rho_{D}}{d t}+3 H \delta \rho_{D}-a^{-1} \bar{\rho}{D} \mathbf{q}^{2} \delta u{D}=0 . \
&\frac{d \delta \rho_{B}}{d t}+3 H \delta \rho_{B}-a^{-1} \bar{\rho}{B} \mathbf{q}^{2} \delta u{B}=0 .
\end{aligned}
$$

物理代写|宇宙学作业代写Cosmology代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。