如果你也在 怎样代写电动力学Electrodynamics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。电动力学Electrodynamics研究与运动中的带电体和变化的电场和磁场有关的现象;由于运动的电荷会产生磁场,所以电动力学关注磁、电磁辐射和电磁感应等效应,包括发电机和电动机等实际应用。
电动力学Electrodynamics电动力学的这一领域,通常被称为经典电动力学,是由物理学家詹姆斯-克拉克-麦克斯韦首次系统地解释的。麦克斯韦方程,一组微分方程,非常普遍地描述了这个领域的现象。最近的发展是量子电动力学,它的制定是为了解释电磁辐射与物质的相互作用,量子理论的规律适用于此。物理学家P. A. M. Dirac, W. Heisenberg, 和W. Pauli是制定量子电动力学的先驱者。当所考虑的带电粒子的速度与光速相当时,必须进行涉及相对论的修正;该理论的这个分支被称为相对论电动力学。它被应用于粒子加速器和电子管所涉及的现象,这些电子管承受着高电压和重电流。
my-assignmentexpert™ 电动力学Electrodynamics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的电动力学Electrodynamics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此电动力学Electrodynamics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在物理Physical作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理Physical代写服务。我们的专家在电动力学Electrodynamics代写方面经验极为丰富,各种电动力学Electrodynamics相关的作业也就用不着 说。
我们提供的电动力学Electrodynamics及其相关学科的代写,服务范围广, 其中包括但不限于:
物理代写|电动力学作业代写Electrodynamics代考|Conservation and Invariance of the Electric Charge
As prototype of a local conservation law, i.e. a conservation law based on a continuity equation relative to a certain four-current $j^{\mu}$, we consider the conservation of the electric charge. If the charged matter consists of point-like particles the current is given by (2.16); if conversely the charge is spread out smoothly, as in macroscopic systems, the current will have a generic form. For what follows, the particular form of the current $j^{\mu}(x)$ will be irrelevant in that we will make reference only to the following assumptions:
(1) $j^{\mu}$ is a vector field;
(2) $j^{\mu}$ satisfies the continuity equation $\partial_{\mu} j^{\mu}=0$;
(3) $\lim {|\mathbf{x}| \rightarrow \infty}\left(|\mathbf{x}|^{3} j^{\mu}(t, \mathbf{x})\right)=0$. The meaning of the condition (3) is that for a fixed $t$ the current decreases at spatial infinity more rapidly than $1 /|\mathbf{x}|^{3}$, a property certainly possessed by the expressions (2.109) and (2.110). Assuming that $j^{\mu}$ satisfies the conditions (1)-(3), we now prove that there exists a conserved as well as Lorentz invariant total charge $Q$. The construction of $Q$ follows a standard procedure which consists in integrating the continuity equation over a generic spatial volume $V$ $$ \int{V} \partial_{0} j^{0} d^{3} x=-\int_{V} \nabla \cdot \mathbf{j} d^{3} x
$$
物理代写|电动力学作业代写Electrodynamics代考|Energy-Momentum Tensor and Four-Momentum
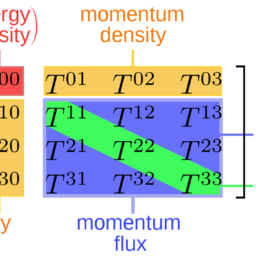
In Sect. 2.4.3 we will show how the conservation of energy and momentum – cornerstone of any fundamental physical theory – occurs in electrodynamics as a consequence of equations (2.20)-(2.22). In this section, before considering this particular case, we set the problem of the realization of these conservation laws in a generic relativistic theory. In a relativistic theory the energy constitutes the fourth component of a four-vector, namely of the four-momentum. Since in such a theory a Lorentz transformation mixes energy and momentum, it is natural to expect that the conservation of the first cannot take place without the simultaneous conservation of the second. So we are looking for four constants of motion, grouped in a four-momentum $P^{\nu}$ whose time component $P^{0}=\varepsilon$ represents the total energy of the system. In line with the conservation paradigm of the electric charge exposed in Sect. 2.4.1, we envisage local conservation laws also for the four-momentum. We require, therefore, each of the four components of $P^{\nu}$ to be associated with a conserved four-current $j^{\mu(\nu)}(x)$. These four currents altogether form a double tensor called energy-momentum tensor – which commonly is denoted by the symbol
$$
T^{\mu \nu}=j^{\mu(\nu)}
$$
As for the electric charge, we postulate that in a relativistic theory the conservation of the four-momentum occurs as consequence of the existence of an energymomentum tensor $T^{\mu \nu}(x)$, possessing the following properties:
(1) $T^{\mu \nu}$ is a tensor field;
(2) $T^{\mu \nu}$ satisfies the continuity equation $\partial_{\mu} T^{\mu \nu}=0$;
(3) $\lim _{|\mathbf{x}| \rightarrow \infty}\left(|\mathbf{x}|^{3} T^{\mu \nu}(t, \mathbf{x})\right)=0$.
物理代写|电动力学作业代写ELECTRODYNAMICS代考|Energy-Momentum Tensor in Electrodynamics
In this section we provide a constructive proof of the existence in the electrodynamics of point-like particles of an energy-momentum tensor $T^{\mu \nu}$ with the properties (1)-(3) postulated in Sect. 2.4.2. We first derive heuristically the form of the energy density $T^{00}$, and then we resort to Lorentz invariance to reconstruct the whole tensor. We begin recalling the known expression of the energy density of the electromagnetic field
$$
T_{\mathrm{em}}^{00}=\frac{1}{2}\left(E^{2}+B^{2}\right) .
$$
Obviously the conserved total energy cannot simply be given by the integral of $T_{\mathrm{em}}^{00}$, because the electromagnetic field exchanges energy with the charged particles. To quantify this exchange we calculate the time derivative of $T_{\mathrm{em}}^{00}$, using the Maxwell equations in the form (2.52)-(2.55):
$$
\begin{aligned}
\frac{\partial T_{\mathrm{em}}^{00}}{\partial t} &=\mathbf{E} \cdot \frac{\partial \mathbf{E}}{\partial t}+\mathbf{B} \cdot \frac{\partial \mathbf{B}}{\partial t}=\mathbf{E} \cdot(\boldsymbol{\nabla} \times \mathbf{B}-\mathbf{j})-\mathbf{B} \cdot \boldsymbol{\nabla} \times \mathbf{E} \
&=-\mathbf{j} \cdot \mathbf{E}-\boldsymbol{\nabla} \cdot(\mathbf{E} \times \mathbf{B})
\end{aligned}
$$
电动力学代写
物理代写|电动力学作业代写ELECTRODYNAMICS代考|CONSERVATION AND INVARIANCE OF THE ELECTRIC CHARGE
作为局部守恒定律的原型,即基于关于某四流的连续性方程的守恒定律jμ,我们考虑电荷守恒。如果带电物质由点状粒子组成,则电流由下式给出2.16; 相反,如果电荷平稳地分布,就像在宏观系统中一样,电流将具有通用形式。接下来,电流的特定形式jμ(X)将无关紧要,因为我们将仅参考以下假设:
(1) $j^{\mu}$ is a vector field;
(2) $j^{\mu}$ satisfies the continuity equation $\partial_{\mu} j^{\mu}=0$;
(3) $\lim {|\mathbf{x}| \rightarrow \infty}\left(|\mathbf{x}|^{3} j^{\mu}(t, \mathbf{x})\right)=0$. The meaning of the condition (3) is that for a fixed $t$ the current decreases at spatial infinity more rapidly than $1 /|\mathbf{x}|^{3}$, a property certainly possessed by the expressions (2.109) and (2.110). Assuming that $j^{\mu}$ satisfies the conditions (1)-(3), we now prove that there exists a conserved as well as Lorentz invariant total charge $Q$. The construction of $Q$ follows a standard procedure which consists in integrating the continuity equation over a generic spatial volume $V$ $$ \int{V} \partial_{0} j^{0} d^{3} x=-\int_{V} \nabla \cdot \mathbf{j} d^{3} x
$$
物理代写|电动力学作业代写ELECTRODYNAMICS代考|ENERGY-MOMENTUM TENSOR AND FOUR-MOMENTUM
昆虫。2.4.3 我们将展示能量和动量守恒——任何基本物理理论的基石——如何作为方程的结果出现在电动力学中2.20-2.22. 在本节中,在考虑这个特殊情况之前,我们将这些守恒定律的实现问题放在一个广义相对论中。在相对论理论中,能量构成四向量的第四个分量,即四动量。由于在这样一个理论中,洛伦兹变换混合了能量和动量,因此很自然地可以预期,如果不同时存在第二个守恒,第一个守恒就不可能发生。所以我们正在寻找四个运动常数,分组为四个动量磷ν谁的时间分量磷0=e代表系统的总能量。符合 Sect 中暴露的电荷守恒范式。2.4.1,我们设想当地的自然保护法也适用于四动量。因此,我们需要以下四个组成部分中的每一个磷ν与守恒的四电流相关联jμ(ν)(X). 这四个电流共同形成了一个双张量,称为能量-动量张量——通常用符号表示
吨μν=jμ(ν)
至于电荷,我们假设在相对论中,四动量守恒是能量动量张量存在的结果吨μν(X),具有以下性质:
(1) $T^{\mu \nu}$ is a tensor field;
(2) $T^{\mu \nu}$ satisfies the continuity equation $\partial_{\mu} T^{\mu \nu}=0$;
(3) $\lim _{|\mathbf{x}| \rightarrow \infty}\left(|\mathbf{x}|^{3} T^{\mu \nu}(t, \mathbf{x})\right)=0$.
物理代写|电动力学作业代写ELECTRODYNAMICS代考|ENERGY-MOMENTUM TENSOR IN ELECTRODYNAMICS
在本节中,我们提供了在电动力学中存在能量-动量张量的点状粒子的建设性证明吨μν与属性1-3假设在Sect。2.4.2. 我们首先启发式地推导出能量密度的形式吨00,然后我们求助于洛伦兹不变性来重构整个张量。我们开始回忆电磁场能量密度的已知表达式
吨和米00=12(和2+乙2).
显然,守恒的总能量不能简单地由积分给出吨和米00,因为电磁场与带电粒子交换能量。为了量化这种交换,我们计算时间导数吨和米00, 使用麦克斯韦方程的形式2.52-2.55:
$$
\begin{aligned}
\frac{\partial T_{\mathrm{em}}^{00}}{\partial t} &=\mathbf{E} \cdot \frac{\partial \mathbf{E}}{\partial t}+\mathbf{B} \cdot \frac{\partial \mathbf{B}}{\partial t}=\mathbf{E} \cdot(\boldsymbol{\nabla} \times \mathbf{B}-\mathbf{j})-\mathbf{B} \cdot \boldsymbol{\nabla} \times \mathbf{E} \
&=-\mathbf{j} \cdot \mathbf{E}-\boldsymbol{\nabla} \cdot(\mathbf{E} \times \mathbf{B})
\end{aligned}
$$

物理代写|电动力学作业代写Electrodynamics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。