如果你也在 怎样代写电动力学Electrodynamics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。电动力学Electrodynamics研究与运动中的带电体和变化的电场和磁场有关的现象;由于运动的电荷会产生磁场,所以电动力学关注磁、电磁辐射和电磁感应等效应,包括发电机和电动机等实际应用。
电动力学Electrodynamics电动力学的这一领域,通常被称为经典电动力学,是由物理学家詹姆斯-克拉克-麦克斯韦首次系统地解释的。麦克斯韦方程,一组微分方程,非常普遍地描述了这个领域的现象。最近的发展是量子电动力学,它的制定是为了解释电磁辐射与物质的相互作用,量子理论的规律适用于此。物理学家P. A. M. Dirac, W. Heisenberg, 和W. Pauli是制定量子电动力学的先驱者。当所考虑的带电粒子的速度与光速相当时,必须进行涉及相对论的修正;该理论的这个分支被称为相对论电动力学。它被应用于粒子加速器和电子管所涉及的现象,这些电子管承受着高电压和重电流。
my-assignmentexpert™ 电动力学Electrodynamics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的电动力学Electrodynamics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此电动力学Electrodynamics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在物理Physical作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理Physical代写服务。我们的专家在电动力学Electrodynamics代写方面经验极为丰富,各种电动力学Electrodynamics相关的作业也就用不着 说。
我们提供的电动力学Electrodynamics及其相关学科的代写,服务范围广, 其中包括但不限于:
物理代写|电动力学作业代写Electrodynamics代考|The Fundamental Equations
We introduce now the fundamental equations of electrodynamics in the manifestly covariant form
$$
\begin{aligned}
\frac{d p_{r}^{\mu}}{d s_{r}} &=e_{r} F^{\mu \nu}\left(y_{r}\right) u_{r \nu}, \quad(r=1, \ldots, N), \
\varepsilon^{\mu \nu \rho \sigma} \partial_{\nu} F_{\rho \sigma} &=0, \
\partial_{\mu} F^{\mu \nu} &=j^{\nu} .
\end{aligned}
$$
We shall call these equations Lorentz equations, Bianchi identity, and Maxwell equation, respectively. ${ }^{2}$ The role of these equations is to determine uniquely the fields $F^{\mu \nu}(x)$ and the world lines $y_{r}^{\mu}\left(\lambda_{r}\right)$, once certain initial conditions have been fixed: According to the Newtonian determinism the system of differential equations (2.20)-(2.22) should, in fact, give rise to a well-posed Cauchy probl4em. The Cauchy problem concerning the coordinates $y_{r}^{\mu}$ will be specified in Sect. 2.2.3, whereas the one associated with the Maxwell tensor $F^{\mu \nu}$ will be formulated later on in Sect. 5.1.3. We call the above system of equations fundamental, in that, in principle, any of its solutions should predict a physically observable phenomenon and,conversely, any observed phenomenon occurring in nature should satisfy it. Unfortunately, as we shall see, these expectations are damped by two basic aspects inherent to classical electrodynamics: the spontaneous violation of time-reversal invariance, see Chap. 6, and the ultraviolet divergences inextricably tied to radiation reaction, see Chap. $15 .$
Before proceeding any further, we rewrite the fundamental equations in the traditional three-dimensional notation:
$$
\begin{array}{cl}
\frac{d \mathbf{p}{r}}{d t}=e{r}\left(\mathbf{E}+\mathbf{v}{r} \times \mathbf{B}\right), & \frac{d \varepsilon{r}}{d t}=e_{r} \mathbf{v}_{r} \cdot \mathbf{E} \
\frac{\partial \mathbf{B}}{\partial t}+\boldsymbol{\nabla} \times \mathbf{E}=0, & \boldsymbol{\nabla} \cdot \mathbf{B}=0 \
-\frac{\partial \mathbf{E}}{\partial t}+\nabla \times \mathbf{B}=\mathbf{j}, & \boldsymbol{\nabla} \cdot \mathbf{E}=\rho
\end{array}
$$
物理代写|电动力学作业代写Electrodynamics代考|Parity and Time Reversal
The system of equations (2.20)-(2.22) is manifestly invariant under the proper Lorentz group. In order to establish its invariance under the complete Lorentz group $O(1,3)$ it remains to verify its invariance under the discrete symmetries, i.e. under parity $\mathcal{P}$ and under time reversal $\mathcal{T}$ (see Sect. 1.4.3 and in particular the definitions (1.64) and (1.65)). For this purpose we must establish beforehand the transformation laws under these symmetries of all fundamental variables.
The coordinates $x^{\mu}$ and the world lines $y^{\mu}(\lambda)$ are obviously vectors under $\mathcal{P}$ as well as under $\mathcal{T}$. The proper time
$$
d s=\sqrt{1-v^{2}} d t
$$
is instead a scalar under $\mathcal{P}$ and a pseudoscalar under $\mathcal{T}$, i.e. it changes its sign if one sends $t$ in $-t$. Accordingly, the four-velocity $u^{\mu}=d y^{\mu} / d s$ is a vector under $\mathcal{P}$ and a pseudovector under $\mathcal{T}$, i.e. we have the transformation laws
$$
\mathcal{P}: u^{\prime \mu}=\mathcal{P}{\nu}^{\mu} u^{\nu}, \quad \mathcal{T}: u^{\prime \mu}=-\mathcal{T}{\nu}^{\mu} u^{\nu} .
$$
物理代写|电动力学作业代写ELECTRODYNAMICS代考|Lorentz Equation
In order to simplify the notation we omit the index $r$ and rewrite the Lorentz equation $(2.20)$ in the equivalent form
$$
H^{\mu} \equiv \frac{d p^{\mu}}{d s}-e F^{\mu \nu}(y) u_{\nu}=0
$$
where the electromagnetic field is evaluated along the world line $y^{\mu}=y^{\mu}(\lambda)$ of the particle. Once the field $F^{\mu \nu}(x)$ is known, $(2.33)$ constitutes a system of four ordinary second-order differential equations in the four unknown functions $y^{\mu}(\lambda)$, which in turn are equivalent to the four equations appearing in (2.23). On the other hand, since the variable $\lambda$ appears only through the proper time $s$, these equations are manifestly invariant under reparameterizations. In accordance with our kinematical analysis of Sect. $2.1$ they determine hence the functions $y^{\mu}(\lambda)$ only modulo a reparameterization.
Cauchy problem. We now address the Cauchy problem associated with equations (2.33), also called initial value problem. This equation represents the equation of motion of a particle and, in line with the classical Newtonian determinism, it should determine the position vector $\mathbf{y}(t)$ at each time $t$ in a consistent and unique way, once the initial conditions $\mathbf{y}(0)$ and $\mathbf{v}(0)=\dot{\mathbf{y}}(0)$ have been assigned. To verify the correctness of this hypothesis we take advantage from reparameterization invariance which allows us to choose as parameter the time: $\lambda=t$. In this way the world line takes the form
$$
y^{\mu}(t)=(t, \mathbf{y}(t))
$$
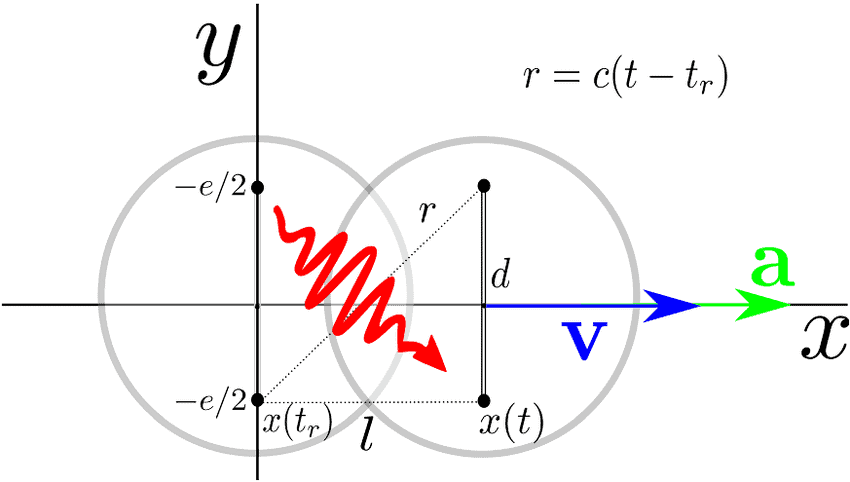
电动力学代写
物理代写|电动力学作业代写ELECTRODYNAMICS代考|THE FUNDAMENTAL EQUATIONS
我们现在以明显的协变形式介绍电动力学的基本方程
dprμdsr=和rFμν(是r)在rν,(r=1,…,ñ), eμνρσ∂νFρσ=0, ∂μFμν=jν.
我们将这些方程分别称为洛伦兹方程、比安奇恒等式和麦克斯韦方程。2这些方程的作用是唯一地确定场Fμν(X)和世界线是rμ(λr),一旦确定了某些初始条件:根据牛顿确定论,微分方程组2.20-2.22事实上,应该引起适定的柯西问题。关于坐标的柯西问题是rμ将在第 3 节中指定。2.2.3,而与麦克斯韦张量相关的Fμν稍后将在 Sect 中制定。5.1.3. 我们称上述方程组为基本方程组,原则上,它的任何解都应该预测物理上可观察到的现象,相反,自然界中发生的任何观察到的现象都应该满足它。不幸的是,正如我们将看到的,这些期望被经典电动力学固有的两个基本方面所抑制:自发违反时间反转不变性,见第 1 章。6,和紫外线发散与辐射反应密不可分,见第 1 章。15.
在继续之前,我们用传统的三维符号重写基本方程:
$$
\begin{array}{cl}
\frac{d \mathbf{p}{r}}{d t}=e{r}\left(\mathbf{E}+\mathbf{v}{r} \times \mathbf{B}\right), & \frac{d \varepsilon{r}}{d t}=e_{r} \mathbf{v}_{r} \cdot \mathbf{E} \
\frac{\partial \mathbf{B}}{\partial t}+\boldsymbol{\nabla} \times \mathbf{E}=0, & \boldsymbol{\nabla} \cdot \mathbf{B}=0 \
-\frac{\partial \mathbf{E}}{\partial t}+\nabla \times \mathbf{B}=\mathbf{j}, & \boldsymbol{\nabla} \cdot \mathbf{E}=\rho
\end{array}
$$
物理代写|电动力学作业代写ELECTRODYNAMICS代考|PARITY AND TIME REVERSAL
方程组2.20-2.22在适当的洛伦兹群下显然是不变的。为了在完全洛伦兹群下建立它的不变性这(1,3)在离散对称下,即在奇偶性下,还有待验证它的不变性磷并且在时间反转下吨 s和和小号和C吨.1.4.3一种nd一世np一种r吨一世C在l一种r吨H和d和F一世n一世吨一世这ns(1.64和1.65)。为此,我们必须事先在所有基本变量的这些对称性下建立变换定律。
该坐标Xμ和世界线是μ(λ)显然是下的向量磷以及下吨. 合适的时间
ds=1−在2d吨
而是一个标量磷和一个伪标量吨,即如果发送,它会改变它的符号吨在−吨. 因此,四速在μ=d是μ/ds是下的向量磷和下的伪向量吨, 即我们有变换定律
$$
\mathcal{P}: u^{\prime \mu}=\mathcal{P} {\nu}^{\mu} u^{\nu}, \quad \mathcal{ T}: u^{\prime \mu}=-\mathcal{T} {\nu}^{\mu} u^{\nu} 。
$$
物理代写|电动力学作业代写ELECTRODYNAMICS代考|LORENTZ EQUATION
为了简化符号,我们省略了索引r并重写洛伦兹方程(2.20)等价形式
Hμ≡dpμds−和Fμν(是)在ν=0
沿着世界线评估电磁场是μ=是μ(λ)的粒子。一旦场Fμν(X)众所周知,(2.33)在四个未知函数中构成一个由四个普通二阶微分方程组成的系统是μ(λ), 这又等价于出现在2.23. 另一方面,由于变量λ只在适当的时候出现s,这些方程在重新参数化下显然是不变的。根据我们对 Sect 的运动学分析。2.1他们因此确定了功能是μ(λ)仅以重新参数化为模。
柯西问题。我们现在解决与方程相关的柯西问题2.33,也称为初值问题。这个方程代表了一个粒子的运动方程,根据经典的牛顿决定论,它应该确定位置向量是(吨)每次吨以一致且独特的方式,一旦初始条件是(0)和在(0)=是˙(0)已分配。为了验证这个假设的正确性,我们利用重新参数化不变性,它允许我们选择时间作为参数:λ=吨. 这样,世界线就形成了

物理代写|电动力学作业代写Electrodynamics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。