如果你也在 怎样代写电路设计Intro to circuit design这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。电路设计Intro to circuit design一个简单的电路由电阻器、电容器、电感器、晶体管、二极管和集成电路组成。这些基本的电子元件是由导电线连接的。电流可以很容易地在这些导线之间流动,以便使电子元件处于工作状态。
电路设计Intro to circuit design过程从规格书开始,规格书说明了成品设计必须提供的功能,但没有指出如何实现这些功能。最初的规格书基本上是对客户希望成品电路实现的技术上的详细描述,可以包括各种电气要求,如电路将接收什么信号,必须输出什么信号,有什么电源,允许消耗多少功率。规格书还可以(通常也是如此)设定设计必须满足的一些物理参数,如尺寸、重量、防潮性、温度范围、热输出、振动容限和加速度容限等。
my-assignmentexpert™ 电路设计Intro to circuit design作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的电路设计Intro to circuit design作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此电路设计Intro to circuit design作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在电子工程Electrical Engineering作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的电子工程Electrical Engineering代写服务。我们的专家在电路设计Intro to circuit design代写方面经验极为丰富,各种电路设计Intro to circuit design相关的作业也就用不着 说。
我们提供的电路设计Intro to circuit design及其相关学科的代写,服务范围广, 其中包括但不限于:
电子工程代写|电路设计作业代写Intro to circuit design代考|Size of the Model
The hyper-parameters that define the number of nodes of an ANN are the number of layers (or depth) of the network and the number of nodes in each layer (or width). In addition, the structure of the connection (fully connected, shared weights, etc.) also affects the total number of parameters to be fitted during the train. The number of nodes in an ANN is an important hyper-parameter and defines the complexity of the function that the ANN can represent. In general, a bigger number of layers (deeper model) will result in an ANN that can learn more complex functions given the same number of nodes [27], but it also increases the complexity of training the network. Deep networks are difficult to train due to numeric instability; namely, issues like the vanishing or exploding gradient can greatly impair the ability to update the weights effectively.
Regarding the number of neurons, it is simple to set the number of units in the input and output layer as they are the number of input and output variables, respectively. However, the hidden layers cause a problem where too many neurons can represent more complex functions but have a negative impact on the training time of the model since the number of weights to be computed increases greatly. There is no objective way to determine the optimal number of neurons in each hidden layer of an ANN. Some heuristics lead to good results in certain problems, but they do not generalize well, making the process of choosing the number of neurons in the hidden layers ultimately a trial-and-error process.
To have a starting point on the number of neurons ( $N_{h}$ for hidden layer $h$ ), some of the heuristics that can be experimented with are:
- For two hidden layer networks, the formulas $N_{h=1}=\sqrt{(m+2) N}+2 \sqrt{\frac{N}{m+2}}$ and $N_{h=2}=\mathrm{m} \sqrt{\frac{N}{m+2}}$, where $\mathrm{N}$ is the number of samples to be learned with low error and $m$ is the number of output variables, are reported to lead to a network that can learn $N$ samples (input-output pairs) with a small error [28].
- In [29], the formula $N_{h=\mathrm{L}}=\frac{N_{\text {in }}+\sqrt{N_{p}}}{L}$ was tested for 40 different test cases. From the obtained results, the authors stated that it can be used to compute the optimum number of neurons in the hidden layers. In this formula, $N_{\text {in }}$ is the number of input neurons, $N_{p}$ is the number of input samples, and $L$ is the number of the hidden layer.
- [30] proposes a theorem to compute the necessary number of hidden units to make the ANN achieve a given approximation order in relation to the function it is trying to model. The approximation order $N$ implies that the derivative of order $N$ at the origin is the same for the function defined by the ANN, $g(x)$ and for the function it is trying to model, $f(x)$, or: $g^{(N)}(0)=f^{(N)}(0)$. To achieve an approximation order $\mathrm{N}$, the number of hidden units across all hidden layers has to follow condition (3.1), where $n_{0}$ is the number of inputs of the model.
$$
\sum_{h=1}^{L} N_{h} \geq \frac{\left(\begin{array}{c}
N+n_{0} \
n_{0}
\end{array}\right)}{n_{0}+2}
$$
when
$$
\left(\begin{array}{c}
N+n_{0} \
n_{0}
\end{array}\right) \leq n_{0}^{2}+3 n_{0}+2 \sqrt{n_{0}^{3}}+4 \sqrt{n_{0}}
$$
otherwise $\sum_{h=1}^{L} N_{h} \geq 2 \sqrt{\left(\begin{array}{c}N+n_{0} \ n_{0}\end{array}\right)+2 n_{0}+2}-n_{0}-3$ - There is some rule of thumb that can be used to choose the total number of hidden neurons, such as:
- The number of hidden neurons should be between the size of the input layer and the size of the output layer;
- The number of hidden neurons should be $2 / 3$ of the size of the input layer plus the size of the output layer;
- The number of hidden neurons should be less than twice the size of the input layer.
- One of the simplest rules is trial and error. It works by training networks with different combinations of the number of units for the hidden layers and saves the one that brings better results. The problem with this method is that it is timeconsuming since training an ANN usually takes a long time. Initially, the number of hidden neurons can be set using one of the heuristics above but in the end, the fine-tuning of these parameters should be adjusted using this method in search of the model that leads to better results.
电子工程代写|电路设计作业代写Intro to circuit design代考|Activation Functions
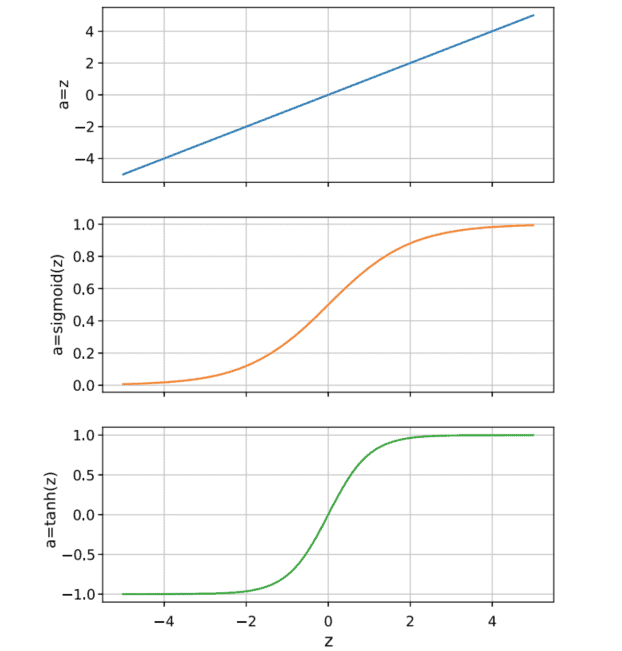
In the early days of ANNs, the most common activation functions are identity, sigmoid, and hyperbolic tangent, shown in Fig. 3.4. Identity is used only at the output layer on regression problems so that the output of the model can be any value (positive or not). In the hidden layers, however, the use of nonlinear functions makes it possible to represent any function using ANNs, and the sigmoid and the hyperbolic tangent started being used as the activation functions because they follow the behavior of biological neurons [8].
However, in 2010 , Glorot and Bengio [31] concluded that the vanishing/exploding gradient problem was caused by a poor choice of the activation function. Following this discovery, a new family of activation functions was proposed. It started with the rectified linear unit (ReLU) activation [32], as described in (3.2). The ReLU works better in deep networks because it does not saturate for positive values; besides, both function and gradient are very easy to compute.
$$
\operatorname{ReLU}(z)=\max (0, z)
$$
Still, once the sum of the weighted inputs of a neuron becomes negative, the neuron will output 0 with a gradient also of zero, which can lead to an average gradient of zero easily, once that happens those weights are no longer updated, leading to a problem known as the dying ReLUs. Some variants of the ReLU were proposed to address this problem. The leaky $\operatorname{Re} L U(\operatorname{lReLU})$ is defined according to (3.3).
$$
l \operatorname{ReLU}(z)=\max (\alpha z, z)
$$
电子工程代写|电路设计作业代写INTRO TO CIRCUIT DESIGN代考|How ANNs “Learn”
The learning, or training, process of an ANN corresponds to solving the optimization problem of finding the model’s parameters that minimize some measure of the model’s error, J. The two most common error functions are mean squared error (MSE) and the mean absolute error (MAE), as defined in (3.5), where $M$ is the number of samples, $x_{i}$ is the input vector, $y_{i}$ is the expected output, and $w$ is the model’s weights.
$$
\begin{aligned}
&\operatorname{MSE}(x, y, w)=\frac{1}{M} \sum_{i=1}^{M}\left(\operatorname{ANN}\left(x_{i}, w\right)-y_{i}\right)^{2} \
&\operatorname{MAE}(x, y, w)=\frac{1}{M} \sum_{i=1}^{M}\left|\operatorname{ANN}\left(x_{i}, w\right)-y_{i}\right|
\end{aligned}
$$
The methods used to solve this optimization problem are based on gradient descent [35], an iterative process where the cost function is travelled in the opposite direction of the gradient. In the case of ANNs’ training, the gradient of the cost function with respect to the weights is computed effectively using backpropagation [5]. During training, the derivative of the error with respect to each weight is propagated backward through the network (hence the name backpropagation) and it is used to update the weights according to (3.6).
$$
w^{(n+1)}=w^{(n)}-\eta \frac{\partial J}{\partial w}\left(w^{(n)}\right)
$$
where $J$ is the cost function, $w$ is a generic weight, $w^{(n+1)}$ represents the value of that weight when it gets updated, and $\eta$ is a scalar called learning step. Backpropagation exploits the chain rule and introduces an easy way to recursively computing the gradient of the cost function given the derivate of the activation functions. The backpropagation rule is represented in (3.7), where $u_{w}$ is the input of the weight’s $w$ net in the feed-forward network and $v_{w}$ is the input of that weight’s net in the backpropagation network.
$$
\frac{\partial J}{\partial w}\left(w^{(n)}\right)=u_{w} v_{w}
$$
电路设计作业代写
电子工程代写|电路设计作业代写INTRO TO CIRCUIT DESIGN代考|SIZE OF THE MODEL
定义 ANN 节点数量的超参数是层数这rd和p吨H网络的数量和每层的节点数这r在一世d吨H. 此外,连接结构F在ll是C这nn和C吨和d,sH一种r和d在和一世GH吨s,和吨C.还会影响训练期间要拟合的参数总数。ANN 中的节点数量是一个重要的超参数,它定义了 ANN 可以表示的函数的复杂性。一般来说,层数较多d和和p和r米这d和l在给定相同数量的节点的情况下,将产生一个可以学习更复杂函数的 ANN27,但也增加了训练网络的复杂度。由于数值不稳定,深度网络难以训练;即,梯度消失或爆炸等问题会极大地影响有效更新权重的能力。
关于神经元的数量,设置输入和输出层中的单元数量很简单,因为它们分别是输入和输出变量的数量。然而,隐藏层会导致一个问题,即过多的神经元可以表示更复杂的函数,但对模型的训练时间有负面影响,因为要计算的权重数量会大大增加。没有客观的方法来确定 ANN 的每个隐藏层中的最佳神经元数量。一些启发式方法在某些问题上产生了良好的结果,但它们不能很好地泛化,使得选择隐藏层中神经元数量的过程最终成为一个反复试验的过程。
在神经元数量上有一个起点$ñH$F这rH一世dd和nl一种是和r$H$,一些可以试验的启发式方法是:
- 对于两个隐藏层网络,公式ñH=1=(米+2)ñ+2ñ米+2和ñH=2=米ñ米+2, 在哪里ñ是要以低误差学习的样本数,并且米是输出变量的数量,被报告导致可以学习的网络ñ样品一世np在吨−这在吨p在吨p一种一世rs有一个小错误28.
- 在29, 公式ñH=大号=ñ在 +ñp大号对 40 个不同的测试用例进行了测试。从获得的结果来看,作者表示它可以用来计算隐藏层中神经元的最佳数量。在这个公式中,ñ在 是输入神经元的数量,ñp是输入样本的数量,并且大号是隐藏层的数量。
- 30提出了一个定理来计算必要的隐藏单元数量,以使 ANN 实现与其试图建模的函数相关的给定近似阶数。近似顺序ñ意味着阶的导数ñ对于 ANN 定义的函数,原点是相同的,G(X)对于它试图建模的功能,F(X), 或者:G(ñ)(0)=F(ñ)(0). 实现近似顺序ñ,所有隐藏层的隐藏单元数量必须遵循条件3.1, 在哪里n0是模型的输入数。
∑H=1大号ñH≥(ñ+n0 n0)n0+2
什么时候
(ñ+n0 n0)≤n02+3n0+2n03+4n0
除此以外∑H=1大号ñH≥2(ñ+n0 n0)+2n0+2−n0−3 - 有一些经验法则可用于选择隐藏神经元的总数,例如:
- 隐藏神经元的数量应该在输入层的大小和输出层的大小之间;
- 隐藏神经元的数量应该是2/3输入层的大小加上输出层的大小;
- 隐藏神经元的数量应小于输入层大小的两倍。
- 最简单的规则之一是反复试验。它的工作原理是使用隐藏层单元数量的不同组合来训练网络,并保存带来更好结果的网络。这种方法的问题在于它很耗时,因为训练 ANN 通常需要很长时间。最初,可以使用上述启发式方法之一设置隐藏神经元的数量,但最后,应使用此方法调整这些参数的微调,以寻找导致更好结果的模型。
电子工程代写|电路设计作业代写INTRO TO CIRCUIT DESIGN代考|ACTIVATION FUNCTIONS
在 ANN 的早期,最常见的激活函数是恒等函数、S 型函数和双曲正切函数,如图 3.4 所示。标识仅用于回归问题的输出层,因此模型的输出可以是任何值p这s一世吨一世在和这rn这吨. 然而,在隐藏层中,非线性函数的使用使得使用 ANN 表示任何函数成为可能,并且 sigmoid 和双曲正切开始被用作激活函数,因为它们遵循生物神经元的行为8.
然而,在 2010 年,Glorot 和 Bengio31得出的结论是,梯度消失/爆炸问题是由激活函数选择不当引起的。在这一发现之后,提出了一个新的激活函数家族。它从整流线性单元开始R和大号在激活32,如中所述3.2. ReLU 在深度网络中效果更好,因为它不会对正值饱和;此外,函数和梯度都非常容易计算。
恢复(和)=最大限度(0,和)
尽管如此,一旦神经元的加权输入之和变为负数,神经元将输出 0,梯度也为零,这很容易导致平均梯度为零,一旦发生这种情况,这些权重不再更新,导致一个被称为垂死 ReLU 的问题。ReLU 的一些变体被提出来解决这个问题。漏水的关于大号在(lReLU)根据定义3.3.
l恢复(和)=最大限度(一种和,和)
电子工程代写|电路设计作业代写INTRO TO CIRCUIT DESIGN代考|HOW ANNS “LEARN”
ANN 的学习或训练过程对应于解决优化问题,即找到模型参数以最小化模型误差 J 的某些度量。两个最常见的误差函数是均方误差米小号和和平均绝对误差米一种和, 如定义3.5, 在哪里米是样本数,X一世是输入向量,是一世是预期输出,并且在是模型的权重。
MSE(X,是,在)=1米∑一世=1米(人工神经网络(X一世,在)−是一世)2 很多(X,是,在)=1米∑一世=1米|人工神经网络(X一世,在)−是一世|
用于解决此优化问题的方法基于梯度下降35,一个迭代过程,其中成本函数在梯度的相反方向上传播。在人工神经网络训练的情况下,使用反向传播有效地计算成本函数相对于权重的梯度5. 在训练期间,误差相对于每个权重的导数通过网络向后传播H和nC和吨H和n一种米和b一种Cķpr这p一种G一种吨一世这n它用于根据3.6.
在(n+1)=在(n)−这∂Ĵ∂在(在(n))
在哪里Ĵ是成本函数,在是一个通用的重量,在(n+1)表示该权重在更新时的值,并且这是一个称为学习步长的标量。反向传播利用链式规则并引入了一种简单的方法来递归计算给定激活函数的导数的成本函数的梯度。反向传播规则表示为3.7, 在哪里在在是权重的输入在前馈网络中的网络和在在是该权重网络在反向传播网络中的输入。
∂Ĵ∂在(在(n))=在在在在

电子工程代写|电路设计作业代写Intro to circuit design代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。