MY-ASSIGNMENTEXPERT™可以为您提供lse.ac.uk ST310 Machine Learning机器学习课程的代写代考和辅导服务!
这是伦敦政经学校机器学习课程的代写成功案例。
ST310课程简介
Teacher responsible
Dr Joshua Loftus
Availability
This course is compulsory on the BSc in Data Science. This course is available on the BSc in Actuarial Science, BSc in Mathematics with Economics, BSc in Mathematics, Statistics and Business and BSc in Politics and Data Science. This course is available as an outside option to students on other programmes where regulations permit. This course is available with permission to General Course students.
This course cannot be taken with ST309 Elementary Data Analytics.
Prerequisites
The primary focus of this course is on the core machine learning techniques in the context of high-dimensional or large datasets (i.e. big data). The first part of the course covers elementary and important statistical methods including nearest neighbours, linear regression, logistic regression, regularisation, cross-validation, and variable selection. The second part of the course deals with more advanced machine learning methods including regression and classification trees, random forests, bagging, boosting, deep neural networks, k-means clustering and hierarchical clustering. The course will also introduce causal inference motivated by analogy between double machine learning and two-stage least squares. All the topics will be delivered using illustrative real data examples. Students will also gain hands-on experience using R or Python programming languages and software environments for data analysis, computing and visualisation.
ST310 Machine Learning HELP(EXAM HELP, ONLINE TUTOR)
(Hyperplanes) Assume $w$ is an $n$-dimensional vector and $b$ is a scalar. A hyperplane in $\mathbb{R}^n$ is the set $\left{x: x \in \mathbb{R}^n\right.$, s.t. $\left.w^T x+b=0\right}$
a. 1 points $\left(n=2\right.$ example) Draw the hyperplane for $w=[-1,2]^T, b=2$ ? Label your axes.
b. 1 points $\left(n=3\right.$ example) Draw the hyperplane for $w=[1,1,1]^T, b=0$ ? Label your axes.
c. 2 points Given some $x_0 \in \mathbb{R}^n$, find the squared distance to the hyperplane defined by $w^T x+b=0$. In other words, solve the following optimization problem:
$$
\begin{aligned}
& \min _x\left|x_0-x\right|^2 \
& \text { s.t. } w^T x+b=0
\end{aligned}
$$
Hint: if $\widetilde{x}_0$ is the minimizer of the above problem, note that $\left|x_0-\widetilde{x}_0\right|=\left|\frac{w^T\left(x_0-\widetilde{x}_0\right)}{|w|}\right|$. What is $w^T \widetilde{x}_0$ ?
For possibly non-symmetric $\boldsymbol{A}, \boldsymbol{B} \in \mathbb{R}^{n \times n}$ and $c \in \mathbb{R}$, let $f(x, y)=x^T \boldsymbol{A} x+y^T \boldsymbol{B} x+c$. Define $\nabla_z f(x, y)=$ $\left[\begin{array}{llll}\frac{\partial f(x, y)}{\partial z_1} & \frac{\partial f(x, y)}{\partial z_2} & \cdots & \frac{\partial f(x, y)}{\partial z_n}\end{array}\right]^T$
a. 2 points Explicitly write out the function $f(x, y)$ in terms of the components $A_{i, j}$ and $B_{i, j}$ using appropriate summations over the indices.
b. 2 pointsWhat is $\nabla_x f(x, y)$ in terms of the summations over indices and vector notation?
c. 2 points What is $\nabla_y f(x, y)$ in terms of the summations over indices and vector notation?
For the $A, b, c$ as defined in Problem 8, use NumPy to compute (take a screen shot of your answer):
a. 2 points What is $A^{-1}$ ?
b. 1 points What is $A^{-1} b$ ? What is $A c$ ?
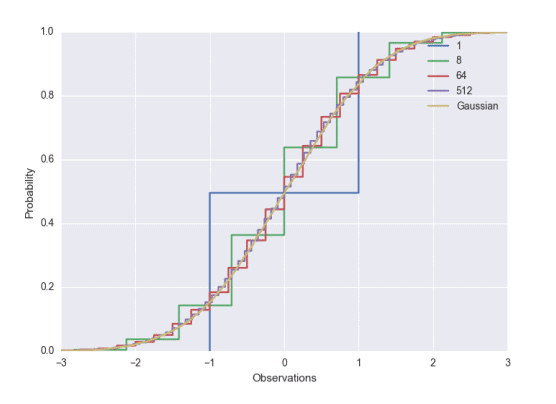
4 points Two random variables $X$ and $Y$ have equal distributions if their CDFs, $F_X$ and $F_Y$, respectively, are equal, i.e. for all $x,\left|F_X(x)-F_Y(x)\right|=0$. The central limit theorem says that the sum of $k$ independent, zero-mean, variance- $1 / k$ random variables converges to a (standard) Normal distribution as $k$ goes off to infinity. We will study this phenomenon empirically (you will use the Python packages Numpy and Matplotlib). Define $Y^{(k)}=\frac{1}{\sqrt{k}} \sum_{i=1}^k B_i$ where each $B_i$ is equal to -1 and 1 with equal probability. From your solution to problem 5 , we know that $\frac{1}{\sqrt{k}} B_i$ is zero-mean and has variance $1 / k$.
a. For $i=1, \ldots, n$ let $Z_i \sim \mathcal{N}(0,1)$. If $F(x)$ is the true CDF from which each $Z_i$ is drawn (i.e., Gaussian) and $\widehat{F}n(x)=\frac{1}{n} \sum{i=1}^n \mathbb{1}\left{Z_i \leq x\right)$, use the answer to problem 1.5 above to choose $n$ large enough such that, for all $x \in \mathbb{R}, \sqrt{\mathbb{E}\left[\left(\widehat{F}_n(x)-F(x)\right)^2\right]} \leq 0.0025$, and plot $\widehat{F}_n(x)$ from -3 to 3 .
Hint: use $\mathrm{Z}=$ numpy.random.randn $(n)$ to generate the random variables, and import matplotlib.pyplot as plt;
plt.step (sorted (Z), np.arange $(1, n+1) / f l o a t(n))$ to plot.
b. For each $k \in{1,8,64,512}$ generate $n$ independent copies $Y^{(k)}$ and plot their empirical CDF on the same plot as part a.
Hint: np.sum (np.sign (np.random.randn $(\mathrm{n}, \mathrm{k})) * n p \cdot \operatorname{sqrt}(1 . / \mathrm{k})$, axis=1) generates $n$ of the $Y^{(k)}$ random variables.
Be sure to always label your axes. Your plot should look something like the following Tip: checkout seaborn for instantly better looking plots.

MY-ASSIGNMENTEXPERT™可以为您提供LSE.AC.UK ST310 MACHINE LEARNING机器学习课程的代写代考和辅导服务!