如果你也在 怎样代写贝叶斯分析Bayesian Analysis 这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。贝叶斯分析Bayesian Analysis一种统计推断方法（以英国数学家托马斯-贝叶斯命名），它允许人们将关于人口参数的先验信息与样本中包含的信息证据相结合，以指导统计推断过程。首先指定一个感兴趣的参数的先验概率分布。然后通过应用贝叶斯定理获得并结合证据，为参数提供一个后验概率分布。后验分布为有关该参数的统计推断提供了基础。

贝叶斯分析Bayesian Analysis自1763年以来，我们现在所知道的贝叶斯统计学并没有一个明确的运行。尽管贝叶斯的方法被拉普拉斯和当时其他领先的概率论者热情地接受，但在19世纪却陷入了不光彩的境地，因为他们还不知道如何正确处理先验概率。20世纪上半叶，一种完全不同的理论得到了发展，现在称为频繁主义统计学。但贝叶斯思想的火焰被少数思想家保持着，如意大利的布鲁诺-德-菲内蒂和英国的哈罗德-杰弗里斯。现代贝叶斯运动开始于20世纪下半叶，由美国的Jimmy Savage和英国的Dennis Lindley带头，但贝叶斯推断仍然极难实现，直到20世纪80年代末和90年代初，强大的计算机开始广泛使用，新的计算方法被开发出来。随后，人们对贝叶斯统计的兴趣大增，不仅导致了贝叶斯方法论的广泛研究，也导致了使用贝叶斯方法来解决天体物理学、天气预报、医疗保健政策和刑事司法等不同应用领域的迫切问题。

同学们在留学期间，都对各式各样的作业考试很是头疼，如果你无从下手，不如考虑my-assignmentexpert™！

my-assignmentexpert™提供最专业的一站式服务：Essay代写，Dissertation代写，Assignment代写，Paper代写，Proposal代写，Proposal代写，Literature Review代写，Online Course，Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务，拥有各个专业的博硕教师团队帮您代写，免费修改及辅导，保证成果完成的效率和质量。同时有多家检测平台帐号，包括Turnitin高级账户，检测论文不会留痕，写好后检测修改，放心可靠，经得起任何考验！

统计代写|贝叶斯分析代考Bayesian Analysis代写|MCMC ALGORITHMS: OVERVIEW

The basic idea of MCMC methods is intuitive. First, a space of states for the random variables of interest is defined; these random variables are those for which we want to draw samples. In Bayesian NLP, these random variables are usually the random variables over which the posterior is defined. Each state in the space corresponds to an assignment of values for all variables. Next, a strategy to explore this space is defined. Each type of MCMC method (whether it is Gibbs sampling, the Metropolis-Hastings or another MCMC method) has a different framework for defining this strategy. Once the strategy is defined, the algorithm works by exploring the space using the strategy until convergence is achieved, and a satisfactory number of samples has been obtained. The samples are collected as the state space is being explored.

If the MCMC method is sound, and the framework it offers is used correctly, there is a theoretical guarantee that the samples being drawn (i.e., the assignment to the random variables according to the state being explored) stem from the distribution the sampler was designed for, such as the posterior. The samples are not necessarily independent. As a matter of fact, in most cases with MCMC algorithms, there is a great dependence between states that were explored in proximity to each other, and thus, between the samples that the algorithm produces. In general, the farther apart the samples drawn are in the chain, the less correlated they are. This observation can be used to generate samples that are closer to being uncorrelated: if $S=\left{y_1, \ldots, y_M\right}$ is a set of correlated samples that were collected for some large $M$, then the subset $\left{y_i \in S \mid i \bmod m=\right.$ $0}$ for some integer $m$ will have samples with weaker correlation (the larger $m$ is, the weaker the correlation). Less formally, we pick a subset of the samples drawn, every $m$ th sample, for some $m$. This process is also called “thinning.”

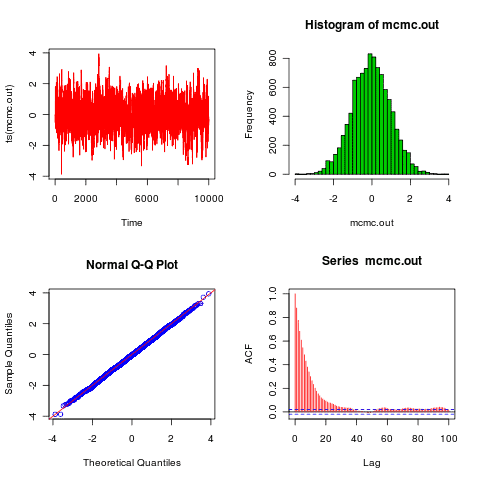
MCMC methods are iterative in nature, with each iteration moving from one state of the sample space to another state. Being iterative, they require some stopping criterion. This stop-ping criterion is of crucial importance with MCMC algorithms-choosing it carelessly could mean that the algorithm never converges, and therefore that all the samples drawn through the algorithm’s execution are not really drawn from the desired posterior. Indeed, in the beginning period of an MCMC algorithm execution, random samples are drawn that are unrelated to the true posterior distribution, in a phase called the burn-in phase. It is sometimes possible to initialize the sampler a certain way so that its burn-in period is shorter. More information about the convergence of MCMC algorithms is discussed in Section 5.7.

统计代写|贝叶斯分析代考Bayesian Analysis代写|NLP MODEL STRUCTURE FOR MCMC INFERENCE

Introductory texts about Bayesian statistics usually consider the inference of the parameters with fully observed data. In NLP, however, most Bayesian statistics are used with latent variables, which means that the posterior is defined over parameters and some predicted structure. This predicted structure is usually a linguistic structure such as a parse tree, an alignment between a pair of trees or sentences or sequence denoting part-of-speech tags.

Since Bayesian NLP usually focuses on latent variable models, inference in this chapter focuses on Bayesian inference with latent variables. This means that the underlying statistical model used has the following structure:
$$
p(\theta, X=x, Z=z \mid \alpha)=p(\theta \mid \alpha) p(Z=z \mid \theta) p(X=x \mid Z=z, \theta) .
$$
In addition, we consider $n$ identically distributed samples (conditionally independent given the model parameters), with a prior at the top level (see Section 3.5). Therefore, the joint distribution values over all random variables in this process are defined as:
$$
p\left(\theta, x^{(1)}, \ldots, x^{(n)}, z^{(1)}, \ldots, z^{(n)} \mid \alpha\right)=p(\theta \mid \alpha)\left(\prod_{i=1}^n p\left(z^{(i)} \mid \theta\right) P\left(x^{(i)} \mid z^{(i)}, \theta\right)\right)
$$
Given that only $x^{(i)}$ for $i \in{1, \ldots, n}$ are observed, the posterior then has the form:

$$
p\left(z^{(1)}, \ldots, z^{(n)}, \theta \mid x^{(1)}, \ldots, x^{(n)}\right) \text {. }
$$
MCMC sampling yields a stream of samples from this posterior, which can be used in various ways, including to find a point estimate for the parameters, to draw predicted structures from the posterior or even to find the maximum value of the posterior using simulated annealing (see Section 5.6). Often, the collapsed setting is of interest, and then samples are drawn from the posterior over the predicted structures only, integrating out the model parameters:
$$
p\left(z^{(1)}, \ldots, z^{(n)} \mid x^{(1)}, \ldots, x^{(n)}\right)=\int_\theta p\left(z^{(1)}, \ldots, z^{(n)}, \theta \mid x^{(1)}, \ldots, x^{(n)}\right) d \theta
$$

贝叶斯分析代写

统计代写|贝叶斯分析代考BAYESIAN ANALYSIS代 写|MCMC ALGORITHMS: OVERVIEW

MCMC 方法的基本思想是直观的。首先，定义感兴找的随机变量的状态空间；这些随机变量是我们要为其抽取样本的变量。在贝叶斯 NLP 中，这 些随机变量通常是定义后验的随机变量。空间中的每个状态对应于所有变量的赋值。接下来，定义探索该空间的策略。每种类型的 MCMC方法 whetheritisGibbssampling, theMetropolis – HastingsoranotherMCMCmethod有一个不同的框架来定义这个策略。一旦定义了策略， 算法就会使用该策略探索空间，直到达到收敛，并获得满意的样本数。在探索状态空间时收集样本。
如果 MCMC 方法是可靠的，并且它提供的框架被正确使用，则理论上可以保证所抽取的样本
i.e., theassignmenttotherandomvariablesaccordingtothestatebeingexplored源于采样器设计的分布，例如后验分布。样本不一定是独立 的。事实上，在使用 MCMC 算法的大多数情况下，在彼此接近的状态之间存在很大的依赖性，因此在算法生成的样本之间存在很大的依赖性。一 关样本，这些样本是为一些大型 $M$, 那么子集 $\backslash$ left[y_i in $S \backslash m i d i \backslash b m o d ~ m=\mid r i g h t . \$ \$ 0}}$ 对于某个整数 $m$ 会有相关性较弱的样本
thelarger $\$ m \$ i s$, theweakerthecorrelation. 不太正式的是，我们选择抽取样本的一个子集，每一个 $m$ 第一个样本，对于一些 $m$. 这个过程也称 为“细化”。

MCMC方法本质上是迭代的，每次迭代从样本空间的一个状态移动到另一个状态。作为迭代，它们需要一些停止标准。这个停止标准对于 MCMC算 法至关重要一一粗心地选择它可能意味着算法永远不会收敛，因此通过算法执行抽取的所有样本并不是真正从期望的后验中抽取的。实际上，在 MCMC 算法执行的开始阶段，在称为老化阶段的阶段中抽取与真实后验分布无关的随机样本。有时可以以某种方式初始化采样器，使其老化时间更 短。有关 MCMC 算法收敛的更多信息在第 5.7 节中讨论。

统计代写|贝叶斯分析代考BAYESIAN ANALYSIS代写|NLP MODEL STRUCTURE FOR MCMC INFERENCE

关于贝叶斯统计的介绍性文本通常考虑使用完全观察到的数据推断参数。然而，在 NLP 中，大多数贝叶斯统计都与潜在变量一起使用，这意味着 后验是在参数和一些预测结构上定义的。这种预测的结构通常是一种语言结构，例如解析树、一对树或句子之间的对齐或表示词性标签的序列。
由于贝叶斯 NLP 通常侧重于潜在变量模型，因此本章的推理侧重于使用潜在变量的贝叶斯推理。这意味着所使用的底层统计模型具有以下结构:
$$
p(\theta, X=x, Z=z \mid \alpha)=p(\theta \mid \alpha) p(Z=z \mid \theta) p(X=x \mid Z=z, \theta) .
$$
此外，我们考虑 $n$ 同分布样本conditionallyindependentgiventhemodelparameters, 在顶层有一个先验seeSection3.5. 因此，该过程中所有 随机变量的联合分布值定义为:
$$
p\left(\theta, x^{(1)}, \ldots, x^{(n)}, z^{(1)}, \ldots, z^{(n)} \mid \alpha\right)=p(\theta \mid \alpha)\left(\prod_{i=1}^n p\left(z^{(i)} \mid \theta\right) P\left(x^{(i)} \mid z^{(i)}, \theta\right)\right)
$$
鉴于只有 $x^{(i)}$ 为了 $i \in 1, \ldots, n$ 被观察到，后验则具有以下形式:
$$
p\left(z^{(1)}, \ldots, z^{(n)}, \theta \mid x^{(1)}, \ldots, x^{(n)}\right)
$$
MCMC 采样从该后验生成一连串样本，可用于多种方式，包括找到参数的点估计，从后验绘制预测结构，甚至使用模拟退火找到后验的最大值 seeSection5.6. 通常，折叠设置很有趣，然后仅从预测结构的后部抽取样本，整合模型参数：
$$
p\left(z^{(1)}, \ldots, z^{(n)} \mid x^{(1)}, \ldots, x^{(n)}\right)=\int_\theta p\left(z^{(1)}, \ldots, z^{(n)}, \theta \mid x^{(1)}, \ldots, x^{(n)}\right) d \theta
$$

统计代写|贝叶斯分析代考Bayesian Analysis代写 请认准exambang™. exambang™为您的留学生涯保驾护航。

微观经济学代写

微观经济学是主流经济学的一个分支，研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富，各种图论代写Graph Theory相关的作业也就用不着 说。

线性代数代写

线性代数是数学的一个分支，涉及线性方程，如：线性图，如：以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。

博弈论代写

现代博弈论始于约翰-冯-诺伊曼（John von Neumann）提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理，这成为博弈论和数学经济学的标准方法。在他的论文之后，1944年，他与奥斯卡-莫根斯特恩（Oskar Morgenstern）共同撰写了《游戏和经济行为理论》一书，该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论，使数理统计学家和经济学家能够处理不确定性下的决策。

微积分代写

微积分，最初被称为无穷小微积分或 “无穷小的微积分”，是对连续变化的数学研究，就像几何学是对形状的研究，而代数是对算术运算的概括研究一样。

它有两个主要分支，微分和积分；微分涉及瞬时变化率和曲线的斜率，而积分涉及数量的累积，以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系，它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。

计量经济学代写

什么是计量经济学？
计量经济学是统计学和数学模型的定量应用，使用数据来发展理论或测试经济学中的现有假设，并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验，然后将结果与被测试的理论进行比较和对比。

根据你是对测试现有理论感兴趣，还是对利用现有数据在这些观察的基础上提出新的假设感兴趣，计量经济学可以细分为两大类：理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。

Matlab代写

MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中，其中问题和解决方案以熟悉的数学符号表示。典型用途包括：数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发，包括图形用户界面构建MATLAB 是一个交互式系统，其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题，尤其是那些具有矩阵和向量公式的问题，而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问，这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展，得到了许多用户的投入。在大学环境中，它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域，MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要，工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数（M 文件）的综合集合，可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。