如果你也在 怎样代写贝叶斯分析Bayesian Analysis 这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。贝叶斯分析Bayesian Analysis一种统计推断方法（以英国数学家托马斯-贝叶斯命名），它允许人们将关于人口参数的先验信息与样本中包含的信息证据相结合，以指导统计推断过程。首先指定一个感兴趣的参数的先验概率分布。然后通过应用贝叶斯定理获得并结合证据，为参数提供一个后验概率分布。后验分布为有关该参数的统计推断提供了基础。

贝叶斯分析Bayesian Analysis自1763年以来，我们现在所知道的贝叶斯统计学并没有一个明确的运行。尽管贝叶斯的方法被拉普拉斯和当时其他领先的概率论者热情地接受，但在19世纪却陷入了不光彩的境地，因为他们还不知道如何正确处理先验概率。20世纪上半叶，一种完全不同的理论得到了发展，现在称为频繁主义统计学。但贝叶斯思想的火焰被少数思想家保持着，如意大利的布鲁诺-德-菲内蒂和英国的哈罗德-杰弗里斯。现代贝叶斯运动开始于20世纪下半叶，由美国的Jimmy Savage和英国的Dennis Lindley带头，但贝叶斯推断仍然极难实现，直到20世纪80年代末和90年代初，强大的计算机开始广泛使用，新的计算方法被开发出来。随后，人们对贝叶斯统计的兴趣大增，不仅导致了贝叶斯方法论的广泛研究，也导致了使用贝叶斯方法来解决天体物理学、天气预报、医疗保健政策和刑事司法等不同应用领域的迫切问题。

同学们在留学期间，都对各式各样的作业考试很是头疼，如果你无从下手，不如考虑my-assignmentexpert™！

my-assignmentexpert™提供最专业的一站式服务：Essay代写，Dissertation代写，Assignment代写，Paper代写，Proposal代写，Proposal代写，Literature Review代写，Online Course，Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务，拥有各个专业的博硕教师团队帮您代写，免费修改及辅导，保证成果完成的效率和质量。同时有多家检测平台帐号，包括Turnitin高级账户，检测论文不会留痕，写好后检测修改，放心可靠，经得起任何考验！

统计代写|贝叶斯分析代考Bayesian Analysis代写|The Dirichlet and Additive Smoothin

Sparse counts need to be carefully handled in language data. For example, it is well-known that distributions over words, or more generally, over $n$-grams, follow a Zipfian distribution; this means that there is a heavy tail of rare $n$-grams, and most of the probability mass is concentrated on a relatively small set of $n$-grams. Since the tail is quite heavy, and includes most of the word types in the language, it cannot be ignored. Yet, it is hard to estimate the probabilities of each element in this tail, because single elements from this tail do not occur often in corpora. Assigning non-zero probability only to $n$-grams that actually occur in the text that we use to estimate the probabilities can lead to zero probabilities for $n$-grams that appear in a held-out dataset. This can be quite detrimental to any model, as it makes the model brittle and not robust to noise. To demonstrate this, consider that if any model assigns zero probability to even a single unseen $n$-gram that occurs when testing the model, the log-likelihood of the whole data diverges to negative infinity. ${ }^2$ More generally, the variance of naïve estimates for $n$-grams that occur infrequently is very large. We turn now to describe a connection between approaches to solve this sparsity issue and the Dirichlet distribution.

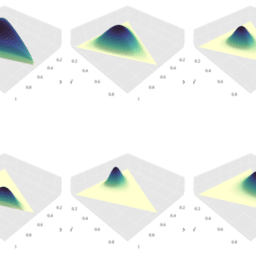
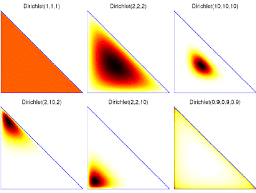
Consider the case in which $\theta$ is drawn from a symmetric Dirichlet, with hyperparameter $\alpha>0$. In addition, $x^{(1)}, \ldots, x^{(n)}$ are drawn from the multinomial distribution $\theta$ (each $x^{(i)} \in$ ${0,1}^K$ is such that $\sum_{j=1}^K x_j^{(i)}=1$ for every $i$ ). In Section 3.2.1, we showed that the posterior $p\left(\theta \mid x^{(1)}, \ldots, x^{(n)}, \alpha\right)$ is also a Dirichlet, with hyperparameters $(\alpha, \alpha, \ldots, \alpha)+\sum_{i=1}^n x^{(i)}$.
The density of the Dirichlet distribution has a single maximum point when all hyperparameters are larger than 1 . In this case, if $\theta^*$ is the posterior maximizer, then:

$$
\theta_j^=\frac{(\alpha-1)+\sum_{i=1}^n x_j^{(i)}}{K(\alpha-1)+\sum_{j=1}^K \sum_{i=1}^n x_j^{(i)}} $$ When $\alpha=1$, the $\alpha-1$ terms in the numerator and the denominator disappear, and we recover the maximum likelihood estimate – the estimate for $\theta^$ is just composed of the relative frequency of each event. Indeed, when $\alpha=1$, the prior $p(\theta \mid \alpha)$ with the Dirichlet is just a uniform non-informative prior, and therefore we recover the MLE .

When $\alpha>1$, the MAP estimation in Equation 4.4 with Dirichlet-multinomial corresponds to a smoothed maximum likelihood estimation. A pseudo-count, $\alpha-1$, is added to each observation. This type of smoothing, also called additive smoothing, or Laplace-Lidstone smoothing, has been regularly used in data-driven NLP since its early days, because it helps to alleviate the problem of sparse counts in language data. With $\alpha<1$, there is a discounting effect, because $\alpha-1<0$.

统计代写|贝叶斯分析代考Bayesian Analysis代写|MAP Estimation and Regularization

There is a strong connection between maximum a posteriori estimation with certain Bayesian priors and a frequentist type of regularization, in which an objective function, such as the loglikelihood, is augmented with a regularization term to avoid overfitting. We now describe this connection with log-linear models.

Log-linear models are a common type of model for supervised problems in NLP. In the generative case, a model is defined on pairs $(x, z)$ where $x$ is the input to the decoding problem and $z$ is the structure to be predicted. The model form is the following:
$$
p(X, Z \mid \theta)=\frac{\exp \left(\sum_{j=1}^K \theta_j f_j(X, Z)\right)}{A(\theta)},
$$
where $f(x, z)=\left(f_1(x, z), \ldots, f_K(x, z)\right)$ is a feature vector that extracts information about the pair $(x, z)$ in order to decide on its probability according to the model.

Each function $f_i(x, z)$ maps $(x, z)$ to $\mathbb{R}$, and is often just a binary function, taking values in ${0,1}$ (to indicate the existence or absence of a sub-structure in $x$ and $z$ ), or integrals, taking values in $\mathbb{N}$ (to count the number of times a certain sub-structure appears in $x$ and $z$ ).

The function $A(\theta)$ is the partition function, defined in order to normalize the distribution:
$$
A(\theta)=\sum_x A(\theta, x)
$$
where
$$
A(\theta, x)=\sum_z \exp \left(\sum_{j=1}^K \theta_j f_j(x, z)\right) .
$$
Alternatively, in a discriminative setting, only the predicted structures are modeled, and the log-linear model is defined as a conditional model:
$$
p(Z \mid X, \theta)=\frac{\exp \left(\sum_{j=1}^K \theta_j f_j(X, Z)\right)}{A(\theta, X)}
$$

贝叶斯分析代写

统计代写|贝叶斯分析代考BAYESIAN ANALYSIS代写|THE DIRICHLET AND ADDITIVE SMOOTHIN

在语言数据中需要小心处理稀疏计数。例如，众所周知，词的分布，或者更一般地， $n$-grams，服从 Zipfian 分布；这意味着有一条稀有的重尾巴 $n$ -grams，并且大部分概率质量集中在相对较小的集合上 $n$-克。由于尾巴很重，包含了该语言中的大部分词类，所以不能忽略。然而，很难估计这 条尾巴中每个元素的概率，因为来自这条尾巴的单个元素在语料库中并不经常出现。仅将非䨐概率分配给 $n$-我们用来估计概率的文本中实际出现 的语法可能导致以下概率为零 $n$-出现在保留数据集中的语法。这对任何模型都非常不利，因为它会使模型变得脆弱并且对噪声不稳健。为了证明 这一点，请考虑如果任何模型将零概率分配给甚至一个看不见的 $n$-gram 在测试模型时出现，整个数据的对数似然发散到负无穷大。 ${ }^2$ 更一般地， 朴素估计的方差 $n$-不经常出现的克非常大。我们现在转而描述解决此稀疏性问题的方法与 Dirichlet 分布之间的联系。
考虑以下情况 $\theta$ 从对称 Dirichlet 中提取，具有超参数 $\alpha>0$. 此外， $x^{(1)}, \ldots, x^{(n)}$ 是从多项分布中得出的 $\theta$ each $\$ x^{(i)} \in \$ \$ 0,1^K \$$ issuchthat $\$ \sum_{j=1}^K x_j^{(i)}=1 \$$ forevery $\$ i$. 在第 3.2 .1 节中，我们展示了后验 $p\left(\theta \mid x^{(1)}, \ldots, x^{(n)}, \alpha\right)$ 也是 Dirichlet，具有 超参数 $(\alpha, \alpha, \ldots, \alpha)+\sum_{i=1}^n x^{(i)}$.
当所有超参数都大于 1 时，Dirichlet 分布的密度有一个最大值点。在这种情况下，如果 $\theta^*$ 是后验最大化器，则：
$$
\theta_j=\frac{(\alpha-1)+\sum_{i=1}^n x_j^{(i)}}{K(\alpha-1)+\sum_{j=1}^K \sum_{i=1}^n x_j^{(i)}}
$$
什么时候 $\alpha=1$ ，这 $\alpha-1$ 分子和分母中的项消失了，我们恢复了最大似然估计一一估计旦只是由每个事件的相对频率组成。的确，当 $\alpha=1$, 先 验的 $p(\theta \mid \alpha)$ 与 Dirichlet 只是一个统一的非信息先验，因此我们恢复了 MLE。
什么时候 $\alpha>1$ ，方程 4.4 中使用 Dirichlet 多项式的 MAP 估计对应于平滑的最大似然估计。一个伪计数， $\alpha-1$, 添加到每个观察。这种类型的平 滑，也称为加法平滑或 Laplace-Lidstone 平滑，从早期开始就经常用于数据驱动的 NLP，因为它有助于缓解语言数据中稀疏计数的问题。和 $\alpha<1$, 存在折扣效应，因为 $\alpha-1<0$.

统计代写|贝叶斯分析代考BAYESIAN ANALYSIS代 与冖|MAP ESTIMATION AND REGULARIZATION

具有某些贝叶斯先验的最大后验估计与频率论类型的正则化之间存在密切联系，其中目标函数（例如对数似然）通过正则化项来增强以避免过度 拟合。我们现在用对数线性模型描述这种联系。
对数线性模型是 NLP 中监督问题的常见模型类型。在生成的情况下，模型是在对上定义的 $(x, z)$ 在哪里 $x$ 是解码问题的输入，并且 $z$ 是要预测的结 构。模型形式如下:
$$
p(X, Z \mid \theta)=\frac{\exp \left(\sum_{j=1}^K \theta_j f_j(X, Z)\right)}{A(\theta)},
$$
在哪里 $f(x, z)=\left(f_1(x, z), \ldots, f_K(x, z)\right)$ 是提取关于对的信息的特征向量 $(x, z)$ 以便根据模型决定其概率。
每个功能 $f_i(x, z)$ 地图 $(x, z)$ 到 $\mathbb{R} ＼mathrm{~ ， 并 且 通 常 只 是 一 个 二 元 函 数 ， 取 值 ~} 0,1$ toindicatetheexistenceorabsenceofasub-structurein $\$ x \$ a n d \$ z \$$ ，或积分，取值 $\mathbb{N}$ tocountthenumberoftimesacertainsub – structureappearsin $\$ x \$ a n d \$ z \$$.
功能 $A(\theta)$ 是配分函数，定义为对分布进行归一化:
$$
A(\theta)=\sum_x A(\theta, x)
$$
在哪里
$$
A(\theta, x)=\sum_z \exp \left(\sum_{j=1}^K \theta_j f_j(x, z)\right) .
$$
或者，在判别设置中，仅对预测结构建模，并将对数线性模型定义为条件模型:
$$
p(Z \mid X, \theta)=\frac{\exp \left(\sum_{j=1}^K \theta_j f_j(X, Z)\right)}{A(\theta, X)}
$$

统计代写|贝叶斯分析代考Bayesian Analysis代写 请认准exambang™. exambang™为您的留学生涯保驾护航。

微观经济学代写

微观经济学是主流经济学的一个分支，研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富，各种图论代写Graph Theory相关的作业也就用不着 说。

线性代数代写

线性代数是数学的一个分支，涉及线性方程，如：线性图，如：以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。

博弈论代写

现代博弈论始于约翰-冯-诺伊曼（John von Neumann）提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理，这成为博弈论和数学经济学的标准方法。在他的论文之后，1944年，他与奥斯卡-莫根斯特恩（Oskar Morgenstern）共同撰写了《游戏和经济行为理论》一书，该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论，使数理统计学家和经济学家能够处理不确定性下的决策。

微积分代写

微积分，最初被称为无穷小微积分或 “无穷小的微积分”，是对连续变化的数学研究，就像几何学是对形状的研究，而代数是对算术运算的概括研究一样。

它有两个主要分支，微分和积分；微分涉及瞬时变化率和曲线的斜率，而积分涉及数量的累积，以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系，它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。

计量经济学代写

什么是计量经济学？
计量经济学是统计学和数学模型的定量应用，使用数据来发展理论或测试经济学中的现有假设，并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验，然后将结果与被测试的理论进行比较和对比。

根据你是对测试现有理论感兴趣，还是对利用现有数据在这些观察的基础上提出新的假设感兴趣，计量经济学可以细分为两大类：理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。

Matlab代写

MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中，其中问题和解决方案以熟悉的数学符号表示。典型用途包括：数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发，包括图形用户界面构建MATLAB 是一个交互式系统，其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题，尤其是那些具有矩阵和向量公式的问题，而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问，这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展，得到了许多用户的投入。在大学环境中，它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域，MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要，工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数（M 文件）的综合集合，可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。