MY-ASSIGNMENTEXPERT™可以为您提供lse.ac.uk ST308 Bayesian Analysis贝叶斯分析课程的代写代考和辅导服务!
这是伦敦政经学校贝叶斯分析课程的代写成功案例。
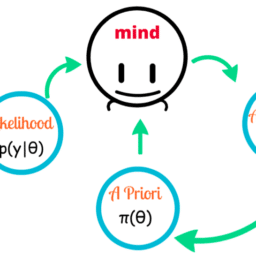
ST308课程简介
This course is available on the BSc in Actuarial Science, BSc in Business Mathematics and Statistics, BSc in Data Science, BSc in Mathematics with Economics and BSc in Mathematics, Statistics and Business. This course is available as an outside option to students on other programmes where regulations permit and to General Course students.
Teaching
This course will be delivered through a combination of classes, lectures, and Q&A sessions, totalling a minimum of 29 hours across the Lent Term. This course does not include a reading week and will be concluded by the end of week 10 of Lent Term.
Prerequisites
Students must have completed one of the following two combinations of courses: (a) ST102 and MA100, or (b) MA107 and ST109 and EC1C1. Equivalent combinations may be accepted at the lecturer’s discretion. ST202 is also recommended.
Previous programming experience is not required but students who have no previous experience in R must complete an online pre-sessional R course from the Digital Skills Lab before the start of the course (https://moodle.lse.ac.uk/course/view.php?id=7745)
ST308 Bayesian Analysis HELP(EXAM HELP, ONLINE TUTOR)
Let $E_1, E_2, E_3$ be events. Let $I_1, I_2, I_3$ be the corresponding indicators so that $I_1=1$ if $E_1$ occurs and $I_1=0$ otherwise.
(a) Let $I_A=1-\left(1-I_1\right)\left(1-I_2\right)$. Verify that $I_A$ is the indicat or for the event $A$ where $A=\left(E_1 \vee E_2\right)$ (that is ” $E_1$ or $E_2$ “) and show that
$$
\operatorname{Pr}(A)=\operatorname{Pr}\left(E_1\right)+\operatorname{Pr}\left(E_2\right)-\operatorname{Pr}\left(E_1 \wedge E_2\right)
$$
where $\left(E_1 \wedge E_2\right)$ is ” $E_1$ and $E_2$ “.
(b) Find a formula, in terms of $I_1, I_2, I_3$ for $I_B$, the indicator for the event $B$ where $B=$ $\left(E_1 \vee E_2 \vee E_3\right)$ and derive a formula for $\operatorname{Pr}(B)$ in terms of $\operatorname{Pr}\left(E_1\right), \operatorname{Pr}\left(E_2\right), \operatorname{Pr}\left(E_3\right), \operatorname{Pr}\left(E_1 \wedge\right.$ $\left.E_2\right), \operatorname{Pr}\left(E_1 \wedge E_3\right), \operatorname{Pr}\left(E_2 \wedge E_3\right), \operatorname{Pr}\left(E_1 \wedge E_2 \wedge E_3\right)$.
In a certain place it rains on one third of the days. The local evening newspaper attempts to predict whether or not it will rain the following day. Three quarters of rainy days and three fifths of dry days are correctly predicted by the previous evening’s paper. Given that this evening’s paper predicts rain, what is the probability that it will actually rain tomorrow?
A machine is built to make mass-produced items. Each item made by the machine has a probability $p$ of being defective. Given the value of $p$, the items are independent of each other. Because of the way in which the machines are made, $p$ could take one of several values. In fact $p=X / 100$ where $X$ has a discrete uniform distribution on the interval $[0,5]$. The machine is tested by counting the number of items made before a defective is produced. Find the conditional probability distribution of $X$ given that the first defective item is the thirteenth to be made.
There are five machines in a factory. Of these machines, three are working properly and two are defective. Machines which are working properly produce articles each of which has independently a probability of 0.1 of being imperfect. For the defective machines this probability is 0.2 .
A machine is chosen at random and five articles produced by the machine are examined. What is the probability that the machine chosen is defective given that, of the five articles examined, two are imperfect and three are perfect?
A crime has been committed. Assume that the crime was committed by exactly one person, that there are 1000 people who could have committed the crime and that, in the absence of any evidence, these people are all equally likely to be guilty of the crime.
A piece of evidence is found. It is judged that this evidence would have a probability of 0.99 of being observed if the crime were committed by a particular individual, A, but a probability of only 0.0001 of being observed if the crime were committed by any other individual.
Find the probability, given the evidence, that A committed the crime.

MY-ASSIGNMENTEXPERT™可以为您提供LSE.AC.UK ST308 BAYESIAN ANALYSIS贝叶斯分析课程的代写代考和辅导服务!