如果你也在 怎样代写博弈论Game theory 这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。博弈论Game theory在20世纪50年代被许多学者广泛地发展。它在20世纪70年代被明确地应用于进化论，尽管类似的发展至少可以追溯到20世纪30年代。博弈论已被广泛认为是许多领域的重要工具。截至2020年，随着诺贝尔经济学纪念奖被授予博弈理论家保罗-米尔格伦和罗伯特-B-威尔逊，已有15位博弈理论家获得了诺贝尔经济学奖。约翰-梅纳德-史密斯因其对进化博弈论的应用而被授予克拉福德奖。

博弈论Game theory是对理性主体之间战略互动的数学模型的研究。它在社会科学的所有领域，以及逻辑学、系统科学和计算机科学中都有应用。最初，它针对的是两人的零和博弈，其中每个参与者的收益或损失都与其他参与者的收益或损失完全平衡。在21世纪，博弈论适用于广泛的行为关系；它现在是人类、动物以及计算机的逻辑决策科学的一个总称。

同学们在留学期间，都对各式各样的作业考试很是头疼，如果你无从下手，不如考虑my-assignmentexpert™！

my-assignmentexpert™提供最专业的一站式服务：Essay代写，Dissertation代写，Assignment代写，Paper代写，Proposal代写，Proposal代写，Literature Review代写，Online Course，Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务，拥有各个专业的博硕教师团队帮您代写，免费修改及辅导，保证成果完成的效率和质量。同时有多家检测平台帐号，包括Turnitin高级账户，检测论文不会留痕，写好后检测修改，放心可靠，经得起任何考验！

想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。

我们在经济Economy代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的经济Economy代写服务。我们的专家在博弈论Game theory代写方面经验极为丰富，各种博弈论Game theory相关的作业也就用不着 说。

经济代写|博弈论代考Game theory代写|TECHNICAL NOTES

Let’s pause a moment for station identification. I like this sentence, but I suppose that it has no place in a game-theory textbook. So let me take the opportunity to give you an additional definition, a useful result, and a philosophical note. Here is the definition:
For a given node $x$ in a game, a player’s continuation value (also called continuation payoff) is the payoff that this player will eventually get contingent on the path of play passing through node $x$.
Implicit in the notion of continuation value is a theory of how the players will behave at the node in question and all of its successors. This could be any theory of behavior. The continuation value at a node $x$ is thus the payoff at the terminal node that would be reached from $x$ given that the players will behave as specified in the theory.
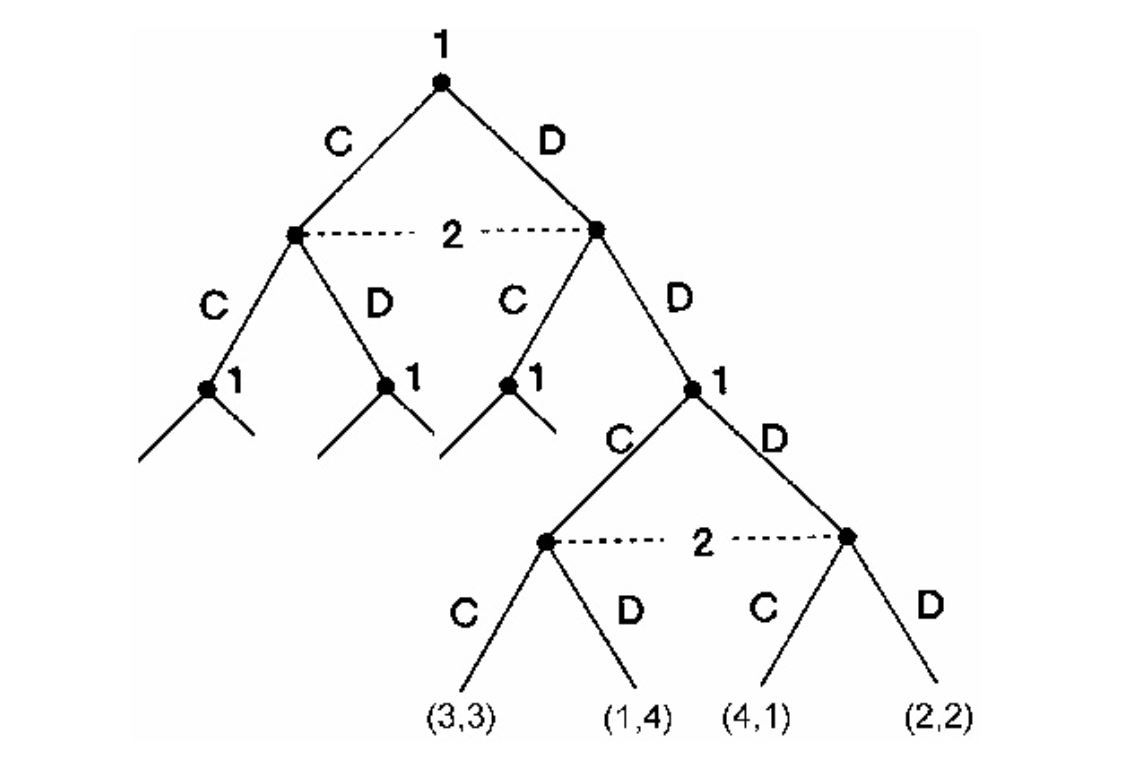
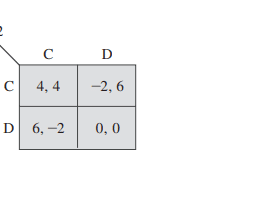
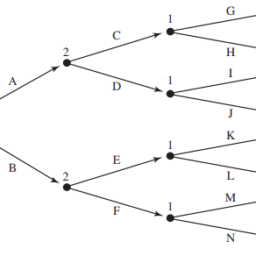
For an illustration, look at the game pictured in Figure 15.2 and let backward induction be our solution concept. We can summarize the rounds of the backward induction procedure in terms of continuation values. The first round of the backward induction procedure establishes that player 1 would select $\mathrm{E}$ at his second decision node. Thus, upon reaching this node, the players anticipate that the game will end with the payoff vector $(3,3)$, so each player’s continuation value is 3 at player 1’s second decision node. Moving backward in the tree, we see that player 2 will get this continuation value if she selects $\mathrm{C}$ at her lower decision node. This value beats the payoff of 2 that she would receive from $D$. Because player 2 would therefore choose $\mathrm{C}$, her continuation value at her lower decision node is 3. Player 1’s continuation payoff is also 3 at this node. Because player 2 would select $\mathrm{A}$ at her upper decision node, player 1’s continuation value is 1 there. At the initial node, player 1 can choose $U$ and get a continuation value of 1 or he can select $\mathrm{D}$ and get a continuation value of 3 , so he selects $D$.
The Stackelberg duopoly game provides another example of continuationvalue calculations. In this example, our behavioral concept can be subgame perfect Nash equilibrium or backward induction (they yield the same results here). As shown earlier in this chapter, contingent on firm 1 selecting a quantity $q_1$, firm 2’s optimal action leads to the payoff vector
$$
\left(\left(6-\frac{q_1}{2}\right) q_1,\left(6-\frac{q_1}{2}\right)^2\right),
$$
so this is the vector of continuation values at firm 2’s information set following firm 1 ‘s selection of $q_1$. At the initial node, firm 1 selects $q_1$ to maximize the continuation value $\left(6-q_1 / 2\right) q_1$.

经济代写|博弈论代考Game theory代写|Conditional Dominance and Forward Induction

I conclude this chapter with an informal presentation of the third basic representation of sequential rationality, a refinement of rationalizability and iterated dominance. The idea is to evaluate best response and dominance conditional on players’ information sets. That is, for a strategy $s_i$ of player $i$, we test whether $s_i$ can be rationalized at each of player $i$ ‘s information sets. We remove $s_i$ from consideration if there is an information set for player $i$ from which $s_i$ is not a best response (or equivalently, is dominated). An iterative removal process gives the implications of common knowledge of sequential rationality.
Recall from Chapter 6 that there is a tight connection between best response and dominance in the normal form. It turns out that the connection extends to the concepts of sequential best response and conditional dominance, which are the sequential-rationality versions of best response and dominance. Adding a common knowledge assumption, these are the basis for extensive-form rationalizability and iterated conditional dominance. 5 I’ll present the iterated conditional dominance construction here because it is simpler to describe and to use in applications … and because I was instrumental in inventing and analyzing it (shameless self-promotion time!).
To define conditional dominance and the iterated procedure, we’ll need a few more definitions. For any extensive-form game of interest, let $H$ denote the set of information sets and let $H^i$ comprise the information sets for player $i$. For any strategy profile $s \in S$ and any information set $h \in H$, we can say that $s$ reaches $h$ if a node in $h$ is on the path through the tree that $s$ induces. In other words, if the players behave as profile $s$ prescribes, then information set $h$ will be reached in the game. Write $S(h)$ as the set of strategy profiles that reach $h$.
Given a nonempty subset of strategy profiles $Y \equiv Y_1 \times Y_2 \times \cdots \times Y_n$, let us say that player $i$ ‘s strategy $s_i$ is dominated in $Y$ if $s_i \in Y_i$ and there is a mixed strategy $\sigma_i \in \Delta Y_i$ such that $u_i\left(\sigma_i, s_{-i}\right)>u_i\left(s_i, s_{-i}\right)$ for each $s_{-i} \in Y_{-i}$. This is just a more formal description of dominance than that shown in Chapter 6 . Here I am being more careful to precisely describe the set of strategies to be used in the payoff comparisons.
In reference to the information sets $H$ and a nonempty subset of strategy profiles $X \equiv X_1 \times X_2 \times \cdots \times X_n$, player $i$ ‘s strategy $s_i$ is said to be conditionally dominated if there is an information set $h \in H^i$ such that $s_i$ is dominated in $X \cap S(h)$.

博弈论代写

经济代写|博弈论代考Game theory代写|TECHNICAL NOTES

让我们暂停一下，辨认一下车站。我喜欢这句话，但我认为它不应该出现在博弈论教科书中。所以让我借此机会给你们一个额外的定义，一个有用的结果，一个哲学的注解。定义如下:
对于游戏中的给定节点$x$，玩家的延续值(也称为延续收益)是该玩家最终通过节点$x$的路径所获得的收益。
延续价值的概念隐含着一种理论，即玩家将如何在相关节点及其所有后续节点上表现。这可以是任何行为理论。因此，节点$x$处的延续值就是从$x$到达的终端节点的收益，假设参与者按照理论中规定的方式行事。
举个例子，看看图15.2所示的游戏，让逆向归纳法作为我们的解决方案概念。我们可以用延拓值来总结逆向归纳过程的轮次。第一轮逆向归纳过程确定玩家1将在第二个决策节点选择$\mathrm{E}$。因此，在到达这个节点后，玩家预期游戏将以收益向量$(3,3)$结束，因此每个玩家在玩家1的第二个决策节点的延续值为3。在树中向后移动，我们看到如果玩家2在其较低的决策节点选择$\mathrm{C}$，她将获得这个延续值。这个值超过了她从$D$得到的2的收益。因为玩家2因此会选择$\mathrm{C}$，所以她在较低决策节点的延续值为3。参与人1在这个节点的延续收益也是3。因为参与人2会在上层决策节点选择$\mathrm{A}$，所以参与人1在那里的延续值为1。在初始节点，参与人1可以选择$U$并获得延续值为1，也可以选择$\mathrm{D}$并获得延续值为3，因此他选择$D$。
Stackelberg双寡头博弈提供了另一个连续值计算的例子。在这个例子中，我们的行为概念可以是子博弈完美纳什均衡或逆向归纳法(它们在这里产生相同的结果)。如本章前面所示，在公司1选择数量$q_1$的情况下，公司2的最优行为导致收益向量
$$
\left(\left(6-\frac{q_1}{2}\right) q_1,\left(6-\frac{q_1}{2}\right)^2\right),
$$
因此，这是公司2的信息集在公司1选择$q_1$后的连续值向量。在初始节点，公司1选择$q_1$使延续值$\left(6-q_1 / 2\right) q_1$最大化。

经济代写|博弈论代考Game theory代写|Conditional Dominance and Forward Induction

我以顺序理性的第三种基本表示的非正式表示来结束本章，这是对可理性化和迭代支配性的改进。其理念是基于玩家的信息集来评估最佳对策和优势。也就是说，对于参与人$i$的策略$s_i$，我们测试$s_i$是否可以在每个参与人$i$的信息集上合理化。如果玩家$i$的信息集中$s_i$不是最佳对策(或劣势)，我们就会从考虑中删除$s_i$。迭代去除过程给出了顺序合理性的共同知识的含义。
回顾第6章，在常态下，最佳反应和支配之间有紧密的联系。事实证明，这种联系延伸到了顺序最佳对策和条件优势的概念，它们是最佳对策和优势的顺序理性版本。加上一个常识假设，这些是广泛形式合理化和迭代条件支配的基础。我将在这里介绍迭代条件支配结构，因为它更容易描述和在应用程序中使用……而且因为我在发明和分析它方面发挥了重要作用(无耻的自我推销时间!)
为了定义条件支配和迭代过程，我们需要更多的定义。对于任何广泛形式的感兴趣的游戏，设$H$表示信息集，并设$H^i$包含玩家$i$的信息集。对于任何策略概要$s \in S$和任何信息集$h \in H$，如果$h$中的一个节点位于$s$诱导的树的路径上，我们可以说$s$到达$h$。换句话说，如果玩家的行为符合个人资料$s$的规定，那么信息集$h$将在游戏中达到。将$S(h)$作为到达$h$的策略配置文件集。
给定策略配置文件$Y \equiv Y_1 \times Y_2 \times \cdots \times Y_n$的非空子集，假设参与人$i$的策略$s_i$在$Y$中占主导地位，如果$s_i \in Y_i$，则存在混合策略$\sigma_i \in \Delta Y_i$，使得$u_i\left(\sigma_i, s_{-i}\right)>u_i\left(s_i, s_{-i}\right)$对应每个$s_{-i} \in Y_{-i}$。这只是比第六章更正式地描述了支配地位。在这里，我将更仔细地精确描述在收益比较中使用的策略集。
参考信息集$H$和策略配置文件$X \equiv X_1 \times X_2 \times \cdots \times X_n$的非空子集，如果存在一个信息集$h \in H^i$使得$s_i$在$X \cap S(h)$中占主导地位，则称玩家$i$的策略$s_i$是有条件劣势的。

经济代写|博弈论代考Game theory代写 请认准exambang™. exambang™为您的留学生涯保驾护航。

微观经济学代写

微观经济学是主流经济学的一个分支，研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富，各种图论代写Graph Theory相关的作业也就用不着 说。

线性代数代写

线性代数是数学的一个分支，涉及线性方程，如：线性图，如：以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。

博弈论代写

现代博弈论始于约翰-冯-诺伊曼（John von Neumann）提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理，这成为博弈论和数学经济学的标准方法。在他的论文之后，1944年，他与奥斯卡-莫根斯特恩（Oskar Morgenstern）共同撰写了《游戏和经济行为理论》一书，该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论，使数理统计学家和经济学家能够处理不确定性下的决策。

微积分代写

微积分，最初被称为无穷小微积分或 “无穷小的微积分”，是对连续变化的数学研究，就像几何学是对形状的研究，而代数是对算术运算的概括研究一样。

它有两个主要分支，微分和积分；微分涉及瞬时变化率和曲线的斜率，而积分涉及数量的累积，以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系，它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。

计量经济学代写

什么是计量经济学？
计量经济学是统计学和数学模型的定量应用，使用数据来发展理论或测试经济学中的现有假设，并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验，然后将结果与被测试的理论进行比较和对比。

根据你是对测试现有理论感兴趣，还是对利用现有数据在这些观察的基础上提出新的假设感兴趣，计量经济学可以细分为两大类：理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。

Matlab代写

MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中，其中问题和解决方案以熟悉的数学符号表示。典型用途包括：数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发，包括图形用户界面构建MATLAB 是一个交互式系统，其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题，尤其是那些具有矩阵和向量公式的问题，而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问，这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展，得到了许多用户的投入。在大学环境中，它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域，MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要，工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数（M 文件）的综合集合，可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。