如果你也在 怎样代写博弈论Game theory 这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。博弈论Game theory在20世纪50年代被许多学者广泛地发展。它在20世纪70年代被明确地应用于进化论，尽管类似的发展至少可以追溯到20世纪30年代。博弈论已被广泛认为是许多领域的重要工具。截至2020年，随着诺贝尔经济学纪念奖被授予博弈理论家保罗-米尔格伦和罗伯特-B-威尔逊，已有15位博弈理论家获得了诺贝尔经济学奖。约翰-梅纳德-史密斯因其对进化博弈论的应用而被授予克拉福德奖。

博弈论Game theory是对理性主体之间战略互动的数学模型的研究。它在社会科学的所有领域，以及逻辑学、系统科学和计算机科学中都有应用。最初，它针对的是两人的零和博弈，其中每个参与者的收益或损失都与其他参与者的收益或损失完全平衡。在21世纪，博弈论适用于广泛的行为关系；它现在是人类、动物以及计算机的逻辑决策科学的一个总称。

同学们在留学期间，都对各式各样的作业考试很是头疼，如果你无从下手，不如考虑my-assignmentexpert™！

my-assignmentexpert™提供最专业的一站式服务：Essay代写，Dissertation代写，Assignment代写，Paper代写，Proposal代写，Proposal代写，Literature Review代写，Online Course，Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务，拥有各个专业的博硕教师团队帮您代写，免费修改及辅导，保证成果完成的效率和质量。同时有多家检测平台帐号，包括Turnitin高级账户，检测论文不会留痕，写好后检测修改，放心可靠，经得起任何考验！

想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。

我们在经济Economy代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的经济Economy代写服务。我们的专家在博弈论Game theory代写方面经验极为丰富，各种博弈论Game theory相关的作业也就用不着 说。

经济代写|博弈论代考Game theory代写|AUCTIONS

In the lemons example, the seller has private information about his and the buyers’ valuations of the good to be traded. Other markets have different information structures. In many instances, prospective buyers have private information about their valuations for the good. Furthermore, different prospective buyers have different tastes, needs, and abilities, leading to variations in people’s willingness to pay for things such as houses, artwork, and productive inputs.
The seller of a good naturally wants to trade at the highest price that she can obtain. When the seller has one object to sell and there are multiple potential buyers, the seller would like to find the buyer with the highest willingness to pay for the object and then consummate a deal with this buyer at a price close to the buyer’s valuation of the good. Unfortunately for the seller, she may not know the prospective buyers’ valuations. One way for the seller to encourage competition between prospective buyers and to identify the highest valuation is to hold an auction.
Auctions are quite common in reality. All sorts of merchandise is sold at formal and informal auction houses, often over the Internet. Many different auction formats are in use as well. There are sealed-bid auctions, where bidders simultaneously and independently submit offers; sealed bids are often used in home sales and for government procurement. There are dynamic oral auctions, where an auctioneer suggests prices in a sequence and the prospective buyers signal or call out their bids. Several versions of these auction forms are in prominent use.
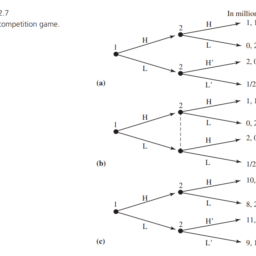
To give you a taste of auction theory and its elemental intuition, I shall present an analysis of three examples of sealed-bid auctions. For the first two, imagine that a person-the seller-has a painting that is worth nothing to her personally. She hopes to make some money by selling the art. There are two potential buyers, whom I call bidders 1 and 2 . Let $v_1$ and $v_2$ denote the valuations of the two bidders. If bidder $i$ wins the painting and has to pay $x$ for it, then bidder $i$ ‘s payoff is $v_i-x$. Suppose that $v_1$ and $v_2$ are chosen independently by nature and that each is uniformly distributed between 0 and 900 . Technically speaking, the probability that $v_i<y$ is $y / 900$. The bidders observe their own valuations before engaging in the auction. However, they do not observe each other’s valuations, so each must bid knowing only his own valuation and that the other’s valuation is distributed uniformly between 0 and 900 . The seller does not observe the bidders’ valuations; she knows only their distributions.

经济代写|博弈论代考Game theory代写|INFORMATION AGGREGATION

The lemon/peach and auction examples just described are cases in which players must make a joint decision (whether and how to trade) based on private information. More generally, there are many situations in which a group, perhaps all of society, must make a collective decision in an environment of incomplete information. For instance, a city may be considering whether to extend a trolley line and, to make the socially optimal choice, it will depend on its individual citizens to report accurately what their own personal costs and benefits from the project would be. Another example is society’s decision as to whether to reelect a president, again optimally a function of the citizens’ individual and privately known preferences. A third example is the question of whether to convict an accused felon, which may be best decided by collecting the various pieces of information that members of a jury have about the defendant and the nature of the crime.
These examples involve information aggregation – that is, combining information from individual players to inform a single decision that affects them all. Such settings are typically called social-choice problems. A key issue in social choice is whether a communication and decision-making rule (known as a mechanism in the technical literature) can be found to achieve social objectives. One component of the analysis is determining the incentives of the players under any given mechanism. Although a formal analysis of general social-choice problems is not a topic for this book, it is worthwhile to examine an applied example to help you recognize nuances in the rational reporting of private information. In plainer language, you will see that players do not always have the incentive to “vote their information.”
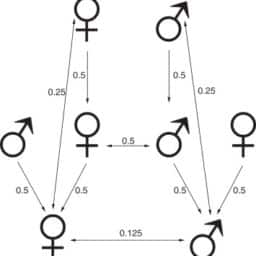
Consider a setting in which a jury must decide whether to acquit or convict a defendant who is on trial. ${ }^8$ For simplicity, suppose that the jury consists of two people who are the players in the game. The defendant’s identity is either guilty or innocent and, from the player’s perspective, this is determined by a move of nature that assigns equal probability to each possibility. During the trial, each juror obtains a signal of the defendant’s identity. Because the jurors have different spheres of expertise and are alert at different times in the trial, the signal that juror/player 1 obtains is independent of the signal that juror/ player 2 obtains. Suppose that each signal is either I or G, with the following distribution: Conditional on an innocent defendant, player $i$ ‘s signal is I with probability $3 / 4$ and $\mathrm{G}$ with probability $1 / 4$. Conditional on a guilty defendant, player $i$ ‘s signal is I with probability $1 / 4$ and $\mathrm{G}$ with probability $3 / 4$. Thus, I is an indication of innocence and $\mathrm{G}$ is an indication of guilt, although neither is absolute.

博弈论代写

经济代写|博弈论代考Game theory代写|AUCTIONS

在柠檬的例子中，卖方有关于他和买方对将要交易的商品的估值的私人信息。其他市场有不同的信息结构。在很多情况下，潜在买家都有自己对商品估值的私人信息。此外，不同的潜在买家有不同的品味、需求和能力，导致人们对房屋、艺术品和生产投入等东西的支付意愿有所不同。商品的卖方自然希望以她能获得的最高价格进行交易。当卖方只有一件物品要出售，而有多个潜在买家时，卖方希望找到最愿意为该物品付款的买家，然后以接近买方对该物品的估价的价格与该买家完成交易。不幸的是，对于卖家来说，她可能不知道潜在买家的估值。卖方鼓励潜在买家之间竞争并确定最高估价的一种方法是举行拍卖。
拍卖在现实中很常见。各种各样的商品在正式和非正式的拍卖行出售，通常是通过互联网。许多不同的拍卖形式也在使用。有闭标拍卖，即竞买人同时独立提交报价;密封投标通常用于房屋销售和政府采购。有动态口头拍卖，拍卖师按顺序提出价格，潜在买家发出信号或喊出他们的出价。这些拍卖形式的几个版本被广泛使用。为了给你一个拍卖理论和它的基本直觉的味道，我将提出三个密封投标拍卖的例子的分析。对于前两种情况，想象一个人——卖家——有一幅对她个人来说毫无价值的画。她希望通过出售这些艺术品赚些钱。有两个潜在的买家，我称他们为竞标者1和2。令$v_1$和$v_2$表示两个竞标者的估价。如果投标人$i赢得了这幅画，并且必须支付$x，那么投标人$i的收益是$v_i-x$。假设$v_1$和$v_2$是自然独立选择的，它们均匀分布在0到900之间。从技术上讲，$v_i<y$的概率是$y / 900$。竞标者在参与拍卖前先观察自己的估价。然而，他们不观察对方的估值，所以每个人都必须只知道自己的估值，而对方的估值均匀分布在0到900之间。卖方不遵守投标人的估价;她只知道它们的分布。

经济代写|博弈论代考Game theory代写|INFORMATION AGGREGATION

在柠檬/桃子和拍卖的例子中，玩家必须根据私人信息共同做出决定(是否以及如何交易)。更一般地说，在许多情况下，一个群体，也许是整个社会，必须在信息不完全的环境中做出集体决策。例如，一个城市可能正在考虑是否延长一条有轨电车线路，为了做出最优的社会选择，这将取决于其公民个人准确地报告他们自己从该项目中获得的成本和收益。另一个例子是社会决定是否重新选举总统，这也是公民个人和私下知道的偏好的最佳函数。第三个例子是是否对被指控的重罪犯定罪的问题，最好的决定方法可能是收集陪审团成员关于被告和犯罪性质的各种信息。
这些例子涉及到信息聚合——也就是说，将来自个体玩家的信息结合起来，形成一个影响所有玩家的单一决策。这种情况通常被称为社会选择问题。社会选择中的一个关键问题是，是否可以找到一种沟通和决策规则(在技术文献中称为一种机制)来实现社会目标。分析的一个组成部分是确定在任何给定机制下参与者的动机。虽然对一般社会选择问题的正式分析不是本书的主题，但检查一个应用示例以帮助您认识到理性报告私人信息中的细微差别是值得的。用更简单的语言来说，你会发现玩家并不总是有动机去“投票他们的信息”。
考虑这样一个场景，陪审团必须决定是无罪释放还是定罪受审的被告。${}^8$为简单起见，假设陪审团由两个人组成，他们是游戏中的玩家。被告的身份要么是有罪的，要么是无辜的，从玩家的角度来看，这是由自然的移动决定的，这种移动为每种可能性分配了相同的概率。在审判过程中，每个陪审员获得被告身份的信号。由于陪审员具有不同的专业知识领域，并且在审判的不同时间保持警觉，因此陪审员/参与人1获得的信号与陪审员/参与人2获得的信号是独立的。假设每个信号为I或G，其分布如下:在无罪被告的条件下，参与人$ I $的信号为I，概率为$3 / 4$和$\ mathm {G}$，概率为$1 / 4$。在被告有罪的条件下，玩家$i$的信号为i，概率为$1 / 4$和$\ mathm {G}$，概率为$3 / 4$。因此，I表示无罪，$\ mathm {G}$表示有罪，尽管两者都不是绝对的。

经济代写|博弈论代考Game theory代写 请认准exambang™. exambang™为您的留学生涯保驾护航。

微观经济学代写

微观经济学是主流经济学的一个分支，研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富，各种图论代写Graph Theory相关的作业也就用不着 说。

线性代数代写

线性代数是数学的一个分支，涉及线性方程，如：线性图，如：以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。

博弈论代写

现代博弈论始于约翰-冯-诺伊曼（John von Neumann）提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理，这成为博弈论和数学经济学的标准方法。在他的论文之后，1944年，他与奥斯卡-莫根斯特恩（Oskar Morgenstern）共同撰写了《游戏和经济行为理论》一书，该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论，使数理统计学家和经济学家能够处理不确定性下的决策。

微积分代写

微积分，最初被称为无穷小微积分或 “无穷小的微积分”，是对连续变化的数学研究，就像几何学是对形状的研究，而代数是对算术运算的概括研究一样。

它有两个主要分支，微分和积分；微分涉及瞬时变化率和曲线的斜率，而积分涉及数量的累积，以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系，它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。

计量经济学代写

什么是计量经济学？
计量经济学是统计学和数学模型的定量应用，使用数据来发展理论或测试经济学中的现有假设，并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验，然后将结果与被测试的理论进行比较和对比。

根据你是对测试现有理论感兴趣，还是对利用现有数据在这些观察的基础上提出新的假设感兴趣，计量经济学可以细分为两大类：理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。

Matlab代写

MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中，其中问题和解决方案以熟悉的数学符号表示。典型用途包括：数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发，包括图形用户界面构建MATLAB 是一个交互式系统，其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题，尤其是那些具有矩阵和向量公式的问题，而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问，这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展，得到了许多用户的投入。在大学环境中，它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域，MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要，工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数（M 文件）的综合集合，可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。