如果你也在 怎样代写投资组合Portfolio Theory 这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。投资组合Portfolio Theory是金融投资的集合，如股票、债券、商品、现金和现金等价物，包括封闭式基金和交易所交易基金（ETF）。人们普遍认为，股票、债券和现金构成了投资组合的核心。

投资组合Portfolio Theory是资产的集合，可以包括股票、债券、共同基金和交易所交易基金等投资。投资组合更像是一个概念，而不是一个物理空间，特别是在数字投资的时代，但把你的所有资产放在一个比喻的屋顶下可能会有帮助。

投资组合Portfolio Theory代写，免费提交作业要求， 满意后付款，成绩80\%以下全额退款，安全省心无顾虑。专业硕 博写手团队，所有订单可靠准时，保证 100% 原创。最高质量的投资组合Portfolio Theory作业代写，服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面，考虑到同学们的经济条件，在保障代写质量的前提下，我们为客户提供最合理的价格。 由于作业种类很多，同时其中的大部分作业在字数上都没有具体要求，因此投资组合Portfolio Theory作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。

同学们在留学期间，都对各式各样的作业考试很是头疼，如果你无从下手，不如考虑my-assignmentexpert™！

my-assignmentexpert™提供最专业的一站式服务：Essay代写，Dissertation代写，Assignment代写，Paper代写，Proposal代写，Proposal代写，Literature Review代写，Online Course，Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务，拥有各个专业的博硕教师团队帮您代写，免费修改及辅导，保证成果完成的效率和质量。同时有多家检测平台帐号，包括Turnitin高级账户，检测论文不会留痕，写好后检测修改，放心可靠，经得起任何考验！

想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。

金融代写|投资组合代写Portfolio Theory代考|A Theoretical Foundation

I think of theory like a map. A map is not reality, of course, but a good map can lead you to your destination much more readily than a bad one. In some cases, the map is accurate but not detailed. We call that a heuristic (or ruleof-thumb). A heuristic works because it is picking up some underlying truth, even though the justification for it may be wrong. Sometimes the map is mostly right, but is wrong in the details. We might be able to use it to get a sense of where we are going, but we may just as easily wind up lost. In other cases, the map is simply wrong, rendering it useless. In that case, we have to throw the map away, explore the unknown area, and draw a new map. As I have witnessed in my own practice, poor theory can lead to poor practical outcomes, but it is not enough to simply decry the map altogether. We must understand why the map is leading us astray. Is it entirely wrong? Or is it simply that the map is not detailed enough? Understanding where and why the map is wrong is an important component to drawing a new one! In my view, traditional portfolio theory is not an entirely useless map (though it is popular to paint it as such). Rather, it is a map that is mostly right some of the time, but often wrong in the details. I see current portfolio theory like one of those early post-Columbian maps showing that North America exists, but not in a way that helps you actually get to North America-the islands and dangerous shoals are not marked, and neither is the shoreline accurately reproduced. The purpose of this chapter is to fill in those details that help us actually get to where we want to be.
Like most models of choice, we must begin with John von Neumann and Oskar Morgenstern’s axioms of rational choice. ${ }^1$ In short, they find that any rational decisions must be consistent with four basic axioms:
A. Complete. For any choices, you must be indifferent to them or prefer one to the other. In other words, you must be able to order your preferences.
B. Transitive. For any choices, if you prefer $A$ to $B$ and you prefer $B$ to $C$, then you must also prefer $A$ to $C$.
C. Continuous. For any choices, there is some factor of your most-liked and most-disliked that you can incorporate to make you indifferent to the middle option. In other words, if you prefer $A$ to $B$ to $C$, then there exits some number, $0 \leq n \leq 1$, such that you are indifferent to getting $n A$ and $(1-n) C$, or getting $B$ by itself.
D. Independent. For any choices, adding some random third choice does not affect your preference. If you prefer $A$ to $B$, you should still prefer getting $A$ and $C$ to $B$ and $C$.

金融代写|投资组合代写Portfolio Theory代考|COMPARISON TO MODERN PORTFOLIO THEORY

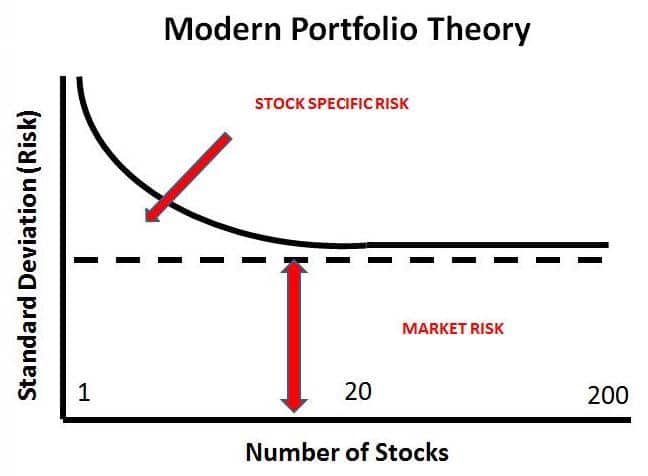
While Markowitz’s work in the 1950 s is often cited as the foundation, modern portfolio theory (MPT) was built by numerous authors (many of whom won Nobel prizes) over the course of two decades. It seems to be a rite of passage for practitioners to level endless criticisms at MPT. However, and despite my own criticisms of the theory, I cannot stress enough how important the ideas of MPT have been to investors! More than anything, MPT gave investors a cohesive framework-a language-within which discussions of portfolio construction were possible. Prior to MPT, portfolio construction was an ad-hoc affair, the aggregate result of many small decisions. The Intelligent Investor, Benjamin Graham’s magnum opus on value investing, for example, has no discussion of how securities should interact within a portfolio! MPT, then, even with all of its flaws, has been a boon to investors. By leveraging quantitative techniques, MPT offers investors a cohesive method for thinking about the management of a portfolio. We also have the benefit of piggybacking on the decades of research by some of the smartest minds in economics. We cannot forget that these original authors did not have such a benefit! Suffice it to say, the goals-based framework would not even exist without the work of these previous authors.
MPT is, rightly, now considered investment orthodoxy. Distilling 20 years and numerous authors down into a discussion that fits within a chapter is fraught with danger, so know that what follows will necessarily be an oversimplification. Even so, I feel it is important to understand where goals-based portfolio theory both connects to and breaks from the dominant framework in existence. If nothing else, we can better appreciate the goals-based framework when we view it in contrast to something-especially something as important as MPT. So, with those preliminaries out of the way, we shall barrel ahead.
While several utility functions exist under the MPT umbrella, the one that drives most portfolio optimization in MPT is the quadratic form of utility:
$$
u=r-\gamma \frac{1}{2} \sigma^2
$$
where $r$ is the expected return of the portfolio, $\sigma^2$ is the portfolio’s variance, and $\gamma$ is the investor’s risk-aversion parameter. Given $\gamma$, and by varying the weights to a portfolio of investments, the optimal balance of portfolio return and variance can be found.

投资组合代写

金融代写|投资组合代写Portfolio Theory代考|A Theoretical Foundation

我认为理论就像地图。当然，地图不是现实，但一张好地图比一张坏地图更容易把你带到目的地。在某些情况下，地图是准确的，但不详细。我们称之为启发式(或经验法则)。启发式之所以有效，是因为它找到了一些潜在的真理，即使它的理由可能是错误的。有时地图大部分是正确的，但在细节上是错误的。我们也许可以用它来知道我们要去哪里，但我们也可能很容易迷路。在其他情况下，地图完全是错误的，导致它毫无用处。在这种情况下，我们必须扔掉地图，探索未知区域，并绘制新地图。正如我在自己的实践中所看到的，糟糕的理论可能导致糟糕的实际结果，但仅仅谴责地图是不够的。我们必须明白为什么地图会把我们引入歧途。这是完全错误的吗?或者仅仅是因为地图不够详细?了解地图在哪里以及为什么是错误的是绘制新地图的重要组成部分!在我看来，传统的投资组合理论并不是一张完全无用的地图(尽管人们普遍这样认为)。相反，它是一幅地图，在某些时候是正确的，但在细节上往往是错误的。在我看来，当前的投资组合理论就像哥伦布发现新大陆后的早期地图一样，虽然北美洲是存在的，但并不能帮助你真正到达北美洲——岛屿和危险的浅滩没有被标记出来，海岸线也没有被精确地复制出来。本章的目的是填补那些帮助我们真正到达我们想要到达的地方的细节。像大多数选择模型一样，我们必须从约翰·冯·诺伊曼和奥斯卡·摩根斯坦的理性选择公理开始。${ }^1$简而言之，他们发现任何理性的决策都必须符合四个基本公理:
A。完成。对于任何一种选择，你必须对它们漠不关心，或者更喜欢其中一个。换句话说，你必须能够订购你的喜好。传递的。对于任何选择，如果您更喜欢$A$而不是$B$，并且更喜欢$B$而不是$C$，那么您也必须更喜欢$A$而不是$C$。连续。对于任何选择，都有一些你最喜欢和最不喜欢的因素，你可以把它们结合起来，让你对中间的选择无动于衷。换句话说，如果你喜欢$A$而不喜欢$B$而不喜欢$C$，那么就会存在一个数字$0 \leq n \leq 1$，这样你就会对获得$n A$和$(1-n) C$或者单独获得$B$漠不关心。独立。对于任何选择，添加一些随机的第三个选择不会影响您的偏好。如果您喜欢$A$而不是$B$，那么您仍然应该更喜欢$A$和$C$而不是$B$和$C$。

金融代写|投资组合代写Portfolio Theory代考|COMPARISON TO MODERN PORTFOLIO THEORY

虽然马科维茨在20世纪50年代的工作经常被引用为基础，但现代投资组合理论(MPT)是由众多作者(其中许多人获得了诺贝尔奖)在20年的时间里建立起来的。对于从业者来说，对MPT提出无休止的批评似乎是一种仪式。然而，尽管我对这一理论提出了批评，但我不能过分强调MPT的思想对投资者的重要性!最重要的是，MPT为投资者提供了一个有凝聚力的框架——一种语言——在这种语言中，可以讨论投资组合的构建。在MPT之前，投资组合构建是一件特别的事情，是许多小决策的汇总结果。例如，本杰明·格雷厄姆(Benjamin Graham)关于价值投资的代表作《聪明的投资者》(Intelligent Investor)就没有讨论证券在投资组合中应该如何相互作用!因此，尽管MPT存在种种缺陷，但它对投资者来说却是一个福音。通过利用定量技术，MPT为投资者提供了一种考虑投资组合管理的有凝聚力的方法。我们还得益于一些最聪明的经济学家几十年来的研究成果。我们不能忘记，这些原作者并没有这样的好处!我只想说，如果没有这些前作者的工作，基于目标的框架甚至不会存在。
MPT现在理所当然地被视为正统的投资理念。将20年的时间和众多作家浓缩到一章的讨论中是充满危险的，所以要知道，接下来的内容必然是过度简化。即便如此，我认为理解基于目标的投资组合理论在哪些方面与现有的主导框架既有联系又有突破是很重要的。如果没有别的，我们可以更好地欣赏基于目标的框架，当我们把它与其他东西——尤其是像MPT这样重要的东西——进行对比时。所以，有了这些预赛，我们将继续前进。
虽然在MPT的保护伞下存在几个效用函数，但在MPT中驱动大多数投资组合优化的是效用的二次形式:
$$
u=r-\gamma \frac{1}{2} \sigma^2
$$
其中$r$为投资组合的预期收益，$\sigma^2$为投资组合的方差，$\gamma$为投资者的风险规避参数。给定$\gamma$，通过改变投资组合的权重，可以找到投资组合收益和方差的最佳平衡。

金融代写|投资组合代写Portfolio Theory代考 请认准exambang™. exambang™为您的留学生涯保驾护航。

微观经济学代写

微观经济学是主流经济学的一个分支，研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富，各种图论代写Graph Theory相关的作业也就用不着 说。

线性代数代写

线性代数是数学的一个分支，涉及线性方程，如：线性图，如：以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。

博弈论代写

现代博弈论始于约翰-冯-诺伊曼（John von Neumann）提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理，这成为博弈论和数学经济学的标准方法。在他的论文之后，1944年，他与奥斯卡-莫根斯特恩（Oskar Morgenstern）共同撰写了《游戏和经济行为理论》一书，该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论，使数理统计学家和经济学家能够处理不确定性下的决策。

微积分代写

微积分，最初被称为无穷小微积分或 “无穷小的微积分”，是对连续变化的数学研究，就像几何学是对形状的研究，而代数是对算术运算的概括研究一样。

它有两个主要分支，微分和积分；微分涉及瞬时变化率和曲线的斜率，而积分涉及数量的累积，以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系，它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。

计量经济学代写

什么是计量经济学？
计量经济学是统计学和数学模型的定量应用，使用数据来发展理论或测试经济学中的现有假设，并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验，然后将结果与被测试的理论进行比较和对比。

根据你是对测试现有理论感兴趣，还是对利用现有数据在这些观察的基础上提出新的假设感兴趣，计量经济学可以细分为两大类：理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。

Matlab代写

MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中，其中问题和解决方案以熟悉的数学符号表示。典型用途包括：数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发，包括图形用户界面构建MATLAB 是一个交互式系统，其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题，尤其是那些具有矩阵和向量公式的问题，而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问，这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展，得到了许多用户的投入。在大学环境中，它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域，MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要，工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数（M 文件）的综合集合，可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。