MY-ASSIGNMENTEXPERT™可以为您提供 handbook MTH3330 Operations research运筹学的代写代考和辅导服务!
这是莫纳什大学 运筹学的代写成功案例。

MATH3330课程简介
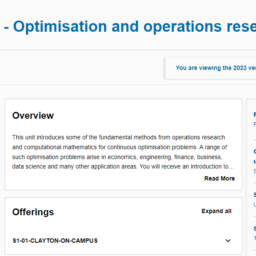
This unit introduces some of the fundamental methods from operations research and computational mathematics for continuous optimisation problems. A range of such optimisation problems arise in economics, engineering, finance, business, data science and many other application areas. You will receive an introduction to the mathematical theory of continuous optimisation with a focus on linear programming methods and smooth non-linear programming. This will broadly include duality theory, the simplex method for linear programming, network optimisation and iterative methods for unconstrained nonlinear optimisation. You will also learn to implement the computational methods efficiently, how to test their implementations for accuracy and performance, and to interpret the results. You will work on optimisation models for applications in a variety of fields. Applications may include examples of supply chain optimisation, economic modelling (including shadow prices), product mix optimisation, portfolio optimisation, parameter estimation and machine learning.
Prerequisites
Enrolment Rule
keyboard_arrow_down
PREREQUISITE: You must have passed one of MTH2051 or MTH3051 or if you are enrolled in the Bachelor of Applied Data Science MTH2019 or both of (MTH2010 or MTH2015) and (MTH2021 or MTH2025) or if you are enrolled in the Honours of Econometrics, ETC2440 (this requires manual enrolment).
Alternatively you must be enrolled in the Master of Financial Mathematics, the Master of Mathematics, or receive special permission from the unit coordinator.
MTH3330 Operations research HELP(EXAM HELP, ONLINE TUTOR)
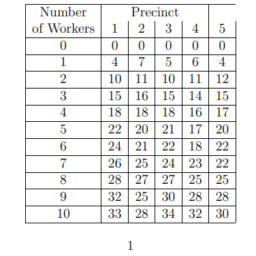
The Campus Social Board in New York budgeted $\$ 1,500,000$ as the bonuses and merits of 503 university teachers. A Salary Differential Evaluation Board, comprising Campus Social Board members, administrators, supervisors and teachers, determined the three variables that should affect bonuses and merits. If we name these variables as $C M_1, C M_2$ and $C M_3$, we obtain:
$C M_1$ : Teachers’ performance measured by the university evaluation instrument. $C M_2$ : General services to the university and its students, including voluntary activities, etc.
$\mathrm{CM}_3$ : Professional development, measured by a formula, which includes teaching merits, research, participation in management tasks, etc.
All three variables above are measured on a scale ranging from 1 (low) to 5 (high). The points scored during 1 year determine bonuses and merits for the following year. In 2001, the sum of the points of these variables was:
$$
\begin{aligned}
& C M_1=1,625 \
& C M_2=1,409 \
& C M_3=1,387
\end{aligned}
$$
The Evaluation Board recommended, and the Campus Social Board accepted, the following rules:
Rule 1: No teacher should receive more than $\$ 5,000$ for bonuses and merits in any given year.
Rule 2: One $C M_1$ variable point is worth twice a $C M_2$ variable point; one $C M_1$ variable point is worth twice a $\mathrm{CM}_3$ variable point.
Rule 3: The value of one of the $C M_1, C M_2, C M_3$ variable points should be as high as possible, but subject to the total budget and to these rules.
(a) Formulate a linear programming model that can establish the optimum value of one of the $C M_1, C M_2, C M_3$ variable points for the year 2002 .
(b) Solve the problem.
(c) Explain the meaning of the results obtained: decision variables, the objective function value and surplus/excess variables.
(a) Formulate a linear programming model that can establish the optimum value of one of the $C M_1, C M_2, C M_3$ variable points for the year 2002.
Decision variables:
$X_1=$ value in dollars of one $C M_1$ variable point
$X_2=$ value in dollars of one $\mathrm{CM}_2$ variable point
$X_3=$ value in dollars of one $\mathrm{CM}_3$ variable point.
Objective function:
$$
\operatorname{Max} z=X_1+X_2+X_3
$$
Constraints:
$$
\begin{aligned}
& \mathrm{C}_1: 5 X_1+5 X_2+5 X_3 \leq 5000(\text { rule } 1) \
& \mathrm{C}_2: 1625 X_1+1409 X_2+1387 X_3 \leq 1500000 \text { (not to exceed the total budget) } \
& \mathrm{C}_3: X_1=2 X_2(\text { rule } 2) \
& \mathrm{C}_4: X_1=2 X_3(\text { rule } 2) \
& X_1, X_2, X_3 \geq 0 \text { (non }- \text { negativity constraint) }
\end{aligned}
$$
(b) Solving the problem.
$$
\begin{aligned}
& \operatorname{Max} z=X_1+X_2+X_3+0 S_1+0 S_2-M A_1-M A_2 \
& \mathrm{C}_1: 5 X_1+5 X_2+5 X_3+\mathrm{S}_1=5000 \
& \mathrm{C}_2: 1625 X_1+1409 X_2+1387 X_3+S_2=1500000 \
& \mathrm{C}_3: X_1-2 X_2+A_1=0 \
& \mathrm{C}_4: X_1-2 X_3+A_2=0
\end{aligned}
$$
(c) Explain the meaning of the results obtained: decision variables, the objective function value and surplus/excess variables Tables (1.1, 1.2, 1.3, 1.4).
Each point of variable $X_1$ is the equivalent to $\$ 496.20$, and each point of variables $X_2$ and $X_3$ is the equivalent to $\$ 248.10$.
Constraint $C_1$ contains a surplus variable, $S_1=38.04$. This implies that the teachers who score $(5,5,5)$, will receive $\$ 38.04$ less than the $\$ 5,000$ fixed as the maximum bonus/merit. In other words, the budgeted amount of $\$ 1,500,000$ would be exhausted if all the teachers scored $(5,5,5)$ and they all received $\$ 5,000$.
A textile firm produces five types of fabric. Each fabric can be woven on one or more of the factory’s 38 looms. The Sales Department has foreseen demand for the forthcoming month. The demand details appear in Table 1.5 along with the data on sale price, variable cost and purchase price, which are per metre and for a width of $140 \mathrm{~cm}$. The factory operates $24 \mathrm{~h} /$ day and is scheduled for 30 days during the following month.
The factory possesses two loom types: jacquard and ratier. Jacquard looms are more versatile and can be used to produce all five fabrics. Ratier looms produce only three of the five fabrics. In all, there are 38 looms: 8 jacquard and 30 ratier. Table 1.6 indicates the production in fabrics of both loom types. The time required to change fabrics is not significant and is not worth considering.
The firm at least meets all the required demand, be it with its own fabrics or with those acquired from another factory. That is to say, the fabrics which cannot be woven in the factory itself, given the loom capacity limitations, will be be acquired from another factory. The purchase price of each fabric also appears in Table 1.5 .
(a) Build a model that can be used to schedule this textile firm’s production and which can also determine how many metres of each fabric must be acquired from the other factory.
(b) The factory is considering acquiring a ninth jacquard loom. In what two ways can profit (if any) be analysed if there is any extra weaving time available? Explain.
(c) How would the model be amended if instead of scheduling production for a single month, the firm had data for the next six months and wished to plan production for these six months?
(a) Build a model to be used to schedule this textile firm’s production and which can also determine how many metres of each fabric must be acquired from the other factory.
Decision variables:
$X 1_J=$ metres of fabric 1 woven on a Jacquard loom
$X_{I A}=$ metres of fabric 1 acquired elsewhere
$X_{2 J}=$ metres of fabric 2 woven on a Jacquard loom
$X_{2 A}=$ metres of fabric 2 acquired elsewhere
$X_{3 J}=$ metres of fabric 3 woven on a Jacquard loom
$X_{3 R}=$ metres of fabric 3 woven on a Ratier loom
$X_{3 A}=$ metres of fabric 3 acquired elsewhere
$X_{4 J}=$ metres of fabric 4 woven on a Jacquard loom
$X_{4 R}=$ metres of fabric 4 woven on a Ratier loom
$X_{4 A}=$ metres of fabric 4 acquired elsewhere
$X_{S J}=$ metres of fabric 5 woven on a Jacquard loom.
$X_{S R}=$ metres of fabric 5 woven on a Ratier loom
$X_{S A}=$ metres of fabric 5 acquired elsewhere.
Objective Function:
$$
\begin{aligned}
\operatorname{Max} z= & 1.33 X_{1 J}+1.13 X_{1 A}+1.31 X_{2 J}+1.16 X_{2 A}+1.61\left(X_{3 J}+X_{3 R}\right)+1.5 X_{3 A} \
& +1.73\left(X_{4 J}+X_{4 R}\right)+1.54 X_{4 A}+1.2\left(X_{5 J}+X_{5 R}\right)+X_{5 A}
\end{aligned}
$$
Constraints:
(Demand constraints)
$$
\begin{aligned}
& X_{1 J}+X_{1 A} \geq 16500 \quad \text { (fabric 1) } \
& X_{2 J}+X_{2 A} \geq 22000 \quad \text { (fabric 2) } \
& X_{3 J}+X_{3 R}+X_{3 A} \geq 62000 \text { (fabric 3) } \
& X_{4 J}+X_{4 R}+X_{4 A} \geq 7500 \text { (fabric 4) } \
& X_{5 J}+X_{5 R}+X_{5 A} \geq 62000 \text { (fabric 5) }
\end{aligned}
$$
(Available capacity constraints)
$$
\begin{aligned}
& X_{1 J} /(4.63 \cdot 24 \cdot 30)+X_{2 J} /(4.63 \cdot 24 \cdot 30)+X_{3 J} /(5.23 \cdot 24 \cdot 30) \
& +X_{4 J} /(5.23 \cdot 24 \cdot 30)+X_{5 J} /(4.17 \cdot 24 \cdot 30) \leq 8 X_{3 R} /(5.23 \cdot 24 \cdot 30) \
& +X_{4 R} /(5.23 \cdot 24 \cdot 30)+X_{5 R} /(4.17 \cdot 24 \cdot 30) \leq 30
\end{aligned}
$$
(Non-negativity constraint)
$$
X_{1 J}, X_{1 A}, X_{2 J}, X_{2 A}, X_{3 J}, X_{3 R}, X_{3 A}, X_{4 J}, X_{4 R}, X_{4 A}, X_{5 J}, X_{5 R}, X_{5 A} \geq 0
$$
(b) The factory is considering acquiring a ninth Jacquard loom. In what two ways can profit (if any) be analysed if there is any additional weaving time available? Explain.
a. It could substitute the capacity restriction for the jacquard loom by the following: $X_{1, J} /(4.63 \cdot 24 \cdot 30)+X_{2, J} /(4.63 \cdot 24 \cdot 30)+X_{3, J} /(5.23 \cdot 24 \cdot 30)$ $+X_{4 . J} /(5.23 \cdot 24 \cdot 30)+X_{5 J} /(4.17 \cdot 24 \cdot 30) \leq 9$, and then solve the problem again.
b. By determining the production resource shadow price of the jacquard looms (the available capacity constraint of the jacquard looms) by either solving the dual problem or starting by analysing the solution obtained by a programme like WinQSB $($ or Solver(B) (Excel).
(c) How would the model be amended if instead of scheduling production for a single month, the firm had data for the next 6 months and wished to plan production for these 6 months?
It would be necessary to define as many decision variables as the quantities to be produced of each fabric on each loom or in each subcontract during each period, which would total to $13 \times 6$ decision variables. Hence, it would be necessary to work with subindices. Besides, if the demand constraints and the available capacity varied according to the period, it would also be necessary to define each one all for all six periods contemplated.
MY-ASSIGNMENTEXPERT™可以为您提供 HANDBOOK MATH3202 OPERATIONS RESEARCH运筹学的代写代考和辅导服务!