如果你也在 怎样代写凸优化Convex optimization 这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。凸优化Convex optimization由于在大规模资源分配、信号处理和机器学习等领域的广泛应用,人们对凸优化的兴趣越来越浓厚。本书旨在解决凸优化问题的算法的最新和可访问的发展。
凸优化Convex optimization无约束可以很容易地用梯度下降(最陡下降的特殊情况)或牛顿方法解决,结合线搜索适当的步长;这些可以在数学上证明收敛速度很快,尤其是后一种方法。[22]如果目标函数是二次函数,也可以使用KKT矩阵技术求解具有线性等式约束的凸优化(它推广到牛顿方法的一种变化,即使初始化点不满足约束也有效),但通常也可以通过线性代数消除等式约束或解决对偶问题来解决。
凸优化Convex optimization代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。 最高质量的凸优化Convex optimization作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此凸优化Convex optimization作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
我们在数学Mathematics代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在凸优化Convex optimization代写方面经验极为丰富,各种凸优化Convex optimization相关的作业也就用不着 说。
数学代写|凸优化代写Convex Optimization代考|CONVERGENCE ANALYSIS OF SUBGRADIENT METHODS
In this section we consider subgradient methods for minimizing a realvalued convex function $f: \Re^n \mapsto \Re$ over a closed convex set $X$. In particular, we focus on methods of the form
$$
x_{k+1}=P_X\left(x_k-\alpha_k g_k\right)
$$
where $g_k$ is any subgradient of $f$ at $x_k, \alpha_k$ is a positive stepsize, and $P_X(\cdot)$ denotes projection on the set $X$ (with respect to the standard Euclidean norm). An important fact here is that by projecting $\left(x_k-\alpha_k g_k\right)$ on $X$, we do not increase the distance to any feasible point, and hence also to any optimal solution, i.e.,
$$
\left|P_X\left(x_k-\alpha_k g_k\right)-x\right| \leq\left|\left(x_k-\alpha_k g_k\right)-x\right|, \quad \forall x \in X .
$$
This is a consequence of the following basic property of the projection.
Proposition 3.2.1: (Nonexpansiveness of the Projection) Let $X$ be a nonempty closed convex set. We have
$$
\left|P_X(x)-P_X(y)\right| \leq|x-y|, \quad \forall x, y \in \mathbb{R}^n .
$$
Proof: From the Projection Theorem (Prop. 1.1.9 in Appendix B),
$$
\left(z-P_X(x)\right)^{\prime}\left(x-P_X(x)\right) \leq 0, \quad \forall z \in X .
$$
Letting $z=P_X(y)$ in this relation, we obtain
$$
\left(P_X(y)-P_X(x)\right)^{\prime}\left(x-P_X(x)\right) \leq 0 .
$$
Similarly,
$$
\left(P_X(x)-P_X(y)\right)^{\prime}\left(y-P_X(y)\right) \leq 0 .
$$
By adding these two inequalities, we see that
$$
\left(P_X(y)-P_X(x)\right)^{\prime}\left(x-P_X(x)-y+P_X(y)\right) \leq 0 .
$$
By rearranging and by using the Schwarz inequality, we have
$$
\left|P_X(y)-P_X(x)\right|^2 \leq\left(P_X(y)-P_X(x)\right)^{\prime}(y-x) \leq\left|P_X(y)-P_X(x)\right| \cdot|y-x|
$$
from which the result follows.
数学代写|凸优化代写Convex Optimization代考|Convergence Analysis
We will now discuss the convergence of the subgradient method (3.13). Throughout our analysis, we denote by $\left{x_k\right}$ the corresponding generated sequence, and we denote by $f^$ and $X^$ the optimal value and optimal solution set, respectively:
$$
f^=\inf {x \in X} f(x), \quad X^=\left{x \in X \mid f(x)=f^*\right} .
$$
We will consider the subgradient method
$$
x{k+1}=P_X\left(x_k-\alpha_k g_k\right),
$$
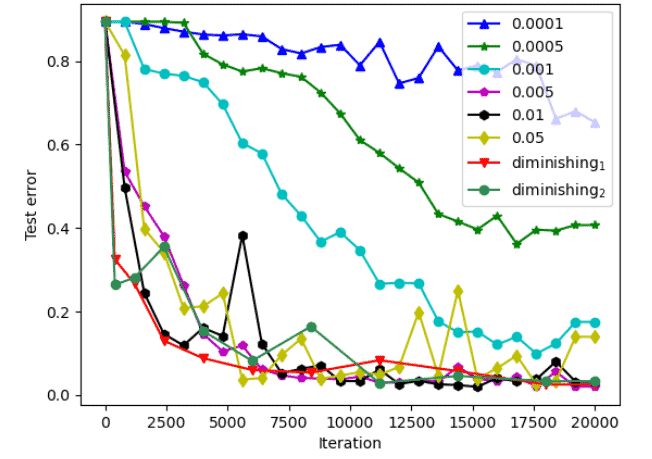
and three different types of rules for selecting the stepsize $\alpha_k$ :
(a) A constant stepsize.
(b) A diminishing stepsize.
(c) A dynamically chosen stepsize based on the optimal value $f^*$ [cf. Prop. 3.2.2(b)] or a suitable estimate.
Additional stepsize rules, and related convergence and rate of convergence results can be found in [NeB00], [NeB01], and [BNO03]. For the first two stepsize rules we will assume the following:
Assumption 3.2.1: (Subgradient Boundedness) For some scalar c) we have
$$
c \geq \sup \left{\left|g_k\right| \mid k=0,1, \ldots\right}
$$
We note that Assumption 3.2.1 is satisfied if $f$ is polyhedral,
$$
f(x)=\max {i=1, \ldots, m}\left{a_i^{\prime} x+b_i\right} $$ an important special case in practice. This is because the subdifferential of such a function at any point $x$ is the convex hull of a subset of $\left{a_1, \ldots, a_m\right}$ [cf. Eq. (3.11)], so in this case we may use $c=\max {i=1, \ldots, m}\left|a_i\right|$ in Assumption 3.2.1. Another important case where Assumption 3.2.1 is satisfied is when $X$ is compact [see Prop. 3.1.2(a)]. More generally, Assumption 3.2.1 will hold if it can be ascertained somehow that $\left{x_k\right}$ is bounded.
凸优化代写
数学代写|凸优化代写Convex Optimization代考|CONVERGENCE ANALYSIS OF SUBGRADIENT METHODS
在本节中,我们考虑在封闭凸集$X$上最小化重值凸函数$f: \Re^n \mapsto \Re$的子梯度方法。我们特别关注表单的方法
$$
x_{k+1}=P_X\left(x_k-\alpha_k g_k\right)
$$
其中$g_k$是$f$的任意子梯度,$x_k, \alpha_k$是正步长,$P_X(\cdot)$表示集合$X$上的投影(相对于标准欧几里得范数)。一个重要的事实是,通过将$\left(x_k-\alpha_k g_k\right)$投影到$X$上,我们不会增加到任何可行点的距离,因此也不会增加到任何最优解的距离,即:
$$
\left|P_X\left(x_k-\alpha_k g_k\right)-x\right| \leq\left|\left(x_k-\alpha_k g_k\right)-x\right|, \quad \forall x \in X .
$$
这是投影的以下基本性质的结果。
命题3.2.1:(投影的非扩张性)设$X$为非空闭凸集。我们有
$$
\left|P_X(x)-P_X(y)\right| \leq|x-y|, \quad \forall x, y \in \mathbb{R}^n .
$$
证明:从投影定理(附录B第1.1.9节),
$$
\left(z-P_X(x)\right)^{\prime}\left(x-P_X(x)\right) \leq 0, \quad \forall z \in X .
$$
让$z=P_X(y)$在这个关系式中,我们得到
$$
\left(P_X(y)-P_X(x)\right)^{\prime}\left(x-P_X(x)\right) \leq 0 .
$$
类似地,
$$
\left(P_X(x)-P_X(y)\right)^{\prime}\left(y-P_X(y)\right) \leq 0 .
$$
把这两个不等式相加,我们看到
$$
\left(P_X(y)-P_X(x)\right)^{\prime}\left(x-P_X(x)-y+P_X(y)\right) \leq 0 .
$$
通过重新排列和使用施瓦茨不等式,我们有
$$
\left|P_X(y)-P_X(x)\right|^2 \leq\left(P_X(y)-P_X(x)\right)^{\prime}(y-x) \leq\left|P_X(y)-P_X(x)\right| \cdot|y-x|
$$
结果由此而来。
数学代写|凸优化代写Convex Optimization代考|Convergence Analysis
现在我们将讨论次梯度法的收敛性(3.13)。在整个分析过程中,我们用$\left{x_k\right}$表示相应生成的序列,用$f^$和$X^$分别表示最优值和最优解集:
$$
f^=\inf {x \in X} f(x), \quad X^=\left{x \in X \mid f(x)=f^\right} . $$ 我们将考虑次梯度法 $$ x{k+1}=P_X\left(x_k-\alpha_k g_k\right), $$ 以及选择步长$\alpha_k$的三种不同类型的规则: (a)一个常数步长。 (b)逐步减小的步长。 (c)基于最优值$f^$[参见Prop. 3.2.2(b)]或合适的估计值动态选择的步长。
在[NeB00]、[NeB01]和[BNO03]中可以找到其他步长规则,以及相关的收敛和收敛速度结果。对于前两个步长规则,我们将假设如下:
假设3.2.1:(次梯度有界性)对于某个标量c)我们有
$$
c \geq \sup \left{\left|g_k\right| \mid k=0,1, \ldots\right}
$$
我们注意到,如果$f$是多面体,则假设3.2.1满足,
$$
f(x)=\max {i=1, \ldots, m}\left{a_i^{\prime} x+b_i\right} $$是实践中的一个重要特例。这是因为这样一个函数在任意一点$x$处的子微分是$\left{a_1, \ldots, a_m\right}$子集的凸包[参见式(3.11)],所以在这种情况下,我们可以在假设3.2.1中使用$c=\max {i=1, \ldots, m}\left|a_i\right|$。另一个满足假设3.2.1的重要情况是$X$是紧实的[见提案3.1.2(a)]。更一般地说,假设3.2.1将成立,如果它能以某种方式确定$\left{x_k\right}$是有界的。

数学代写|凸优化代写Convex Optimization代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。