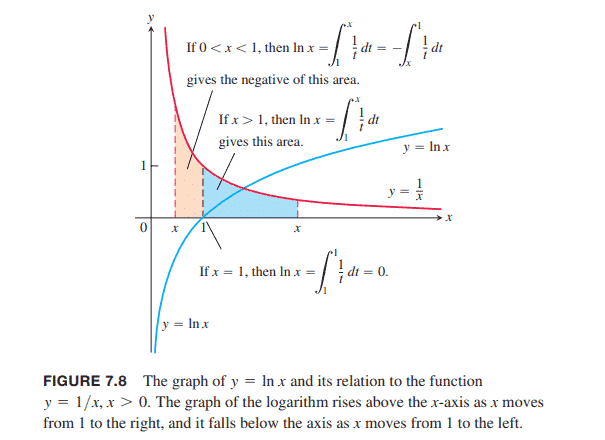
如果你也在 怎样代写微积分Calculus 这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。微积分Calculus 基本上就是非常高级的代数和几何。从某种意义上说,它甚至不是一门新学科——它采用代数和几何的普通规则,并对它们进行调整,以便它们可以用于更复杂的问题。(当然,问题在于,从另一种意义上说,这是一门新的、更困难的学科。)
微积分Calculus数学之所以有效,是因为曲线在局部是直的;换句话说,它们在微观层面上是直的。地球是圆的,但对我们来说,它看起来是平的,因为与地球的大小相比,我们在微观层面上。微积分之所以有用,是因为当你放大曲线,曲线变直时,你可以用正则代数和几何来处理它们。这种放大过程是通过极限数学来实现的。
同学们在留学期间,都对各式各样的作业考试很是头疼,如果你无从下手,不如考虑my-assignmentexpert™!
my-assignmentexpert™提供最专业的一站式服务:Essay代写,Dissertation代写,Assignment代写,Paper代写,Proposal代写,Proposal代写,Literature Review代写,Online Course,Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务,拥有各个专业的博硕教师团队帮您代写,免费修改及辅导,保证成果完成的效率和质量。同时有多家检测平台帐号,包括Turnitin高级账户,检测论文不会留痕,写好后检测修改,放心可靠,经得起任何考验!
微积分Calculus 代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。 最高质量的微积分Calculus 作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此微积分Calculus 作业代写的价格不固定。通常在专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
。
数学代写|微积分代写Calculus代考|Hyperbolic Functions
The basic idea of integration by parts is to transform an integral you can’t do into a simple product minus an integral you can do. Here’s the formula:
Integration by Parts: $\int u d v=u v-\int v d u$
And here’s the method in a nutshell. What’s $\int \sqrt{x} \ln (x) d x$ ? First, you’ve got to split up the integrand into a $u$ and a $d v$ so that it fits the formula. For this problem, choose $\ln (x)$ to be your $u$. Then everything else is the $d v$, namely $\sqrt{x} d x$. (I show you how to choose $u$ in the next section.) Next, you differentiate $u$ to get your $d u$, and you integrate $d v$ to get your $v$. Finally, you plug everything into the formula and you’re home free.
To help keep everything straight, organize integration-by-parts problems with a box like the one on the left in Figure 10-1. For each new problem, draw an empty 2 -by- 2 box, then put your $u$ in the upper-left corner and your $d v$ in the lower-right corner. The box for the above problem is on the right in Figure 10-1.
The arrows in Figure 10-1 remind you to differentiate on the left and to integrate on the right. Now do the calculus and complete the box as shown in Figure 10-2:
$$
\begin{array}{rlrl}
u & =\ln (x) & d v & =\sqrt{x} d x \
\frac{d u}{d x} & =\frac{1}{x} & \int d v & =\int \sqrt{x} d x \
d u & =\frac{1}{x} d x & v & =\frac{2}{3} x^{3 / 2}
\end{array}
$$
数学代写|微积分代写Calculus代考|Derivatives and Integrals of Hyperbolic Functions
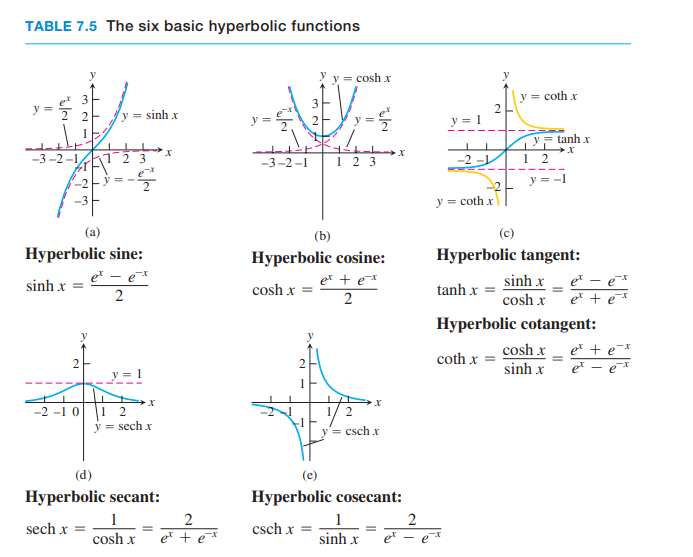
The six hyperbolic functions, being rational combinations of the differentiable functions $e^x$ and $e^{-x}$, have derivatives at every point at which they are defined (Table 7.7). Again, there are similarities with trigonometric functions.
The derivative formulas are derived from the derivative of $e^u$ :
$$
\begin{array}{rlrl}
\frac{d}{d x}(\sinh u) & =\frac{d}{d x}\left(\frac{e^u-e^{-u}}{2}\right) & & \text { Definition of } \sinh u \
& =\frac{e^u d u / d x+e^{-u} d u / d x}{2} & & \text { Derivative of } e^u \
& =\cosh u \frac{d u}{d x} . & \text { Definition of } \cosh u
\end{array}
$$
This gives the first derivative formula. From the definition, we can calculate the derivative of the hyperbolic cosecant function, as follows:
$$
\begin{aligned}
\frac{d}{d x}(\operatorname{csch} u) & =\frac{d}{d x}\left(\frac{1}{\sinh u}\right) & & \text { Definition of } \operatorname{csch} u \
& =-\frac{\cosh u}{\sinh ^2 u} \frac{d u}{d x} & & \text { Quotient Rule for derivatives } \
& =-\frac{1}{\sinh u} \frac{\cosh u}{\sinh u} \frac{d u}{d x} & & \text { Rearrange terms. } \
& =-\operatorname{csch} u \operatorname{coth} u \frac{d u}{d x} & & \text { Definitions of csch } u \text { and coth } u
\end{aligned}
$$
The other formulas in Table 7.7 are obtained similarly.
微积分代写
数学代写|微积分代写Calculus代考|Hyperbolic Functions
分部积分的基本思想是把一个不能做的积分转化成一个简单的乘积减去一个可以做的积分。公式如下:
分部积分:$\int u d v=u v-\int v d u$
简单来说就是这个方法。$\int \sqrt{x} \ln (x) d x$是什么?首先,你必须把被积函数分解成$u$和$d v$,这样才符合公式。对于这个问题,选择$\ln (x)$作为您的$u$。剩下的都是$d v$,也就是$\sqrt{x} d x$。(下一节将向您展示如何选择$u$。)接下来,对$u$进行微分得到$d u$,对$d v$进行积分得到$v$。最后,把所有的东西代入公式,就搞定了。
为了让所有问题保持清晰,可以用图10-1中左边的方框来组织零件集成问题。对于每个新问题,画一个空的2 × 2的方框,然后把$u$放在左上角,$d v$放在右下角。解决上述问题的方框在图10-1的右侧。
图10-1中的箭头提示左侧为求导,右侧为积分。现在进行计算并完成如图10-2所示的方框:
$$
\begin{array}{rlrl}
u & =\ln (x) & d v & =\sqrt{x} d x \
\frac{d u}{d x} & =\frac{1}{x} & \int d v & =\int \sqrt{x} d x \
d u & =\frac{1}{x} d x & v & =\frac{2}{3} x^{3 / 2}
\end{array}
$$
数学代写|微积分代写Calculus代考|Derivatives and Integrals of Hyperbolic Functions
这六个双曲函数是可微函数$e^x$和$e^{-x}$的有理组合,在它们被定义的每一点上都有导数(表7.7)。这和三角函数有相似之处。
导数公式由$e^u$的导数推导而来:
$$
\begin{array}{rlrl}
\frac{d}{d x}(\sinh u) & =\frac{d}{d x}\left(\frac{e^u-e^{-u}}{2}\right) & & \text { Definition of } \sinh u \
& =\frac{e^u d u / d x+e^{-u} d u / d x}{2} & & \text { Derivative of } e^u \
& =\cosh u \frac{d u}{d x} . & \text { Definition of } \cosh u
\end{array}
$$
这是一阶导数公式。根据定义,我们可以计算双曲余割函数的导数,如下:
$$
\begin{aligned}
\frac{d}{d x}(\operatorname{csch} u) & =\frac{d}{d x}\left(\frac{1}{\sinh u}\right) & & \text { Definition of } \operatorname{csch} u \
& =-\frac{\cosh u}{\sinh ^2 u} \frac{d u}{d x} & & \text { Quotient Rule for derivatives } \
& =-\frac{1}{\sinh u} \frac{\cosh u}{\sinh u} \frac{d u}{d x} & & \text { Rearrange terms. } \
& =-\operatorname{csch} u \operatorname{coth} u \frac{d u}{d x} & & \text { Definitions of csch } u \text { and coth } u
\end{aligned}
$$
表7.7中其他公式的推导方法类似。

数学代写|微积分代写Calculus代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。