There are many ways to compare elements of a set other than to say two elements are equal or the same. For example, in the set of people let two people be equivalent if they have the same weight. This would not be saying they were the same person, just that they weighed the same. Often such relations involve considering one characteristic of the elements of a set and then saying the two elements are equivalent if they are the same as far as the given characteristic is concerned.
Definition 3.3.1 Let $S$ be a set. $\sim$ is an equivalence relation on $S$ if it satisfies the following axioms.
- $x \sim x$ for all $x \in S$. (Reflexive)
- If $x \sim y$ then $y \sim x$. (Symmetric)
- If $x \sim y$ and $y \sim z$, then $x \sim z$. (Transitive)
Definition 3.3.2 $[x]$ denotes the set of all elements of $S$ which are equivalent to $x$ and $[x]$ is called the equivalence class determined by $x$ or just the equivalence class of $x$.
With the above definition one can prove the following simple theorem.
Theorem 3.3.3 Let $\sim$ be an equivalence relation defined on a set, $S$ and let $\mathcal{H}$ denote the set of equivalence classes. Then if $[x]$ and $[y]$ are two of these equivalence classes, either $x \sim y$ and $[x]=[y]$ or it is not true that $x \sim y$ and $[x] \cap[y]=\emptyset$.
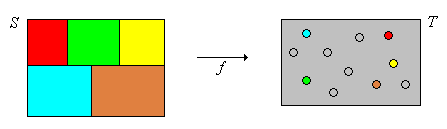
除了说两个元素相等或相同之外,还有很多方法可以比较集合中的元素。例如,在一组人中,如果两个人的体重相同,则假设他们是等价的。这并不是说他们是同一个人,只是说他们的体重相同。通常这样的关系涉及考虑一组元素的一个特征,然后说这两个元素是等价的,如果它们就给定的特征而言是相同的。
定义 3.3.1 令 $S$ 是一个集合。 $\sim$ 是 $S$ 上的等价关系,如果它满足以下公理。
- $x \sim x$ 用于所有 $x \in S$。 (反身的)
- 如果$x \sim y$ 那么$y \sim x$。 (对称)
- 如果$x \sim y$ 和$y \sim z$,则$x \sim z$。 (传递)
定义 3.3.2 $[x]$ 表示 $S$ 中与 $x$ 等价的所有元素的集合,$[x]$ 称为由 $x$ 确定的等价类或只是 $x 的等价类美元。
有了上面的定义,可以证明下面的简单定理。
定理 3.3.3 令 $\sim$ 是定义在集合 $S$ 上的等价关系,令 $\mathcal{H}$ 表示等价类的集合。那么如果 $[x]$ 和 $[y]$ 是这些等价类中的两个,要么 $x \sim y$ 和 $[x]=[y]$ 要么 $x \sim y$ 和$[x] \cap[y]=\emptyset$。

微积分note Integer Multiples of Irrational Numbers 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。