如果你也在 怎样代写博弈论Game theory 这个学科遇到相关的难题，请随时右上角联系我们的24/7代写客服。博弈论Game theory在20世纪50年代被许多学者广泛地发展。它在20世纪70年代被明确地应用于进化论，尽管类似的发展至少可以追溯到20世纪30年代。博弈论已被广泛认为是许多领域的重要工具。截至2020年，随着诺贝尔经济学纪念奖被授予博弈理论家保罗-米尔格伦和罗伯特-B-威尔逊，已有15位博弈理论家获得了诺贝尔经济学奖。约翰-梅纳德-史密斯因其对进化博弈论的应用而被授予克拉福德奖。

博弈论Game theory是对理性主体之间战略互动的数学模型的研究。它在社会科学的所有领域，以及逻辑学、系统科学和计算机科学中都有应用。最初，它针对的是两人的零和博弈，其中每个参与者的收益或损失都与其他参与者的收益或损失完全平衡。在21世纪，博弈论适用于广泛的行为关系；它现在是人类、动物以及计算机的逻辑决策科学的一个总称。

同学们在留学期间，都对各式各样的作业考试很是头疼，如果你无从下手，不如考虑my-assignmentexpert™！

my-assignmentexpert™提供最专业的一站式服务：Essay代写，Dissertation代写，Assignment代写，Paper代写，Proposal代写，Proposal代写，Literature Review代写，Online Course，Exam代考等等。my-assignmentexpert™专注为留学生提供Essay代写服务，拥有各个专业的博硕教师团队帮您代写，免费修改及辅导，保证成果完成的效率和质量。同时有多家检测平台帐号，包括Turnitin高级账户，检测论文不会留痕，写好后检测修改，放心可靠，经得起任何考验！

想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。

我们在经济Economy代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的经济Economy代写服务。我们的专家在博弈论Game theory代写方面经验极为丰富，各种博弈论Game theory相关的作业也就用不着 说。

经济代写|博弈论代考Game theory代写|The Meaning of “Game”

Before we launch into the theory, a note on conflict and cooperation is in order. Most sports and leisure games are considered adversarial contests (in which someone wins and someone loses). However, as already noted, many settings of interdependence do not fit so neatly into this category. In fact, most situations contain elements of conflict as well as elements of potential cooperation or coordination or both. Consider a firm in which two managers interact to develop a new product. Their individual actions may affect each other’s return from the project, so the setting involves interdependence. But must there be a winner and a loser? One can certainly imagine outcomes in which both managers “win” or “lose” to some degree. Perhaps if the managers cooperate with each other in developing the product, both will be likely to gain from the project’s success. On the other hand, each of the managers may have an incentive to provide less effort than the other would prefer.
For another example having elements of both conflict and cooperation, consider a contracting problem between a worker and his employer. They may need to bargain over a wage contract prior to the production of an economic good. Although the interests of the parties may conflict regarding the worker’s wage, their interests may be more aligned on another dimension. For instance, the parties may both prefer that the contract include a bonus for the worker to be granted in the event of exceptional performance on the job, because the bonus may give the worker the right incentive to generate profit that they can share. You may recognize this “concentrate on enlarging the pie” theme as the subject of some fluffy management-oriented books on bargaining. It is nonetheless a good example of how issues of conflict and cooperation arise simultaneously in many settings.
Keeping in mind that conflict and cooperation overlap, I take a broad view of what constitutes a game. In short, games are formal descriptions of strategic settings. Thus, game theory is a methodology of formally studying situations of interdependence. By “formally” I mean using a mathematically precise and logically consistent structure. With the right theoretical tools in place, we can study behavior in a variety of contexts and come to better understand economic and, more generally, social interaction.

经济代写|博弈论代考Game theory代写|Other Examples and Conventions

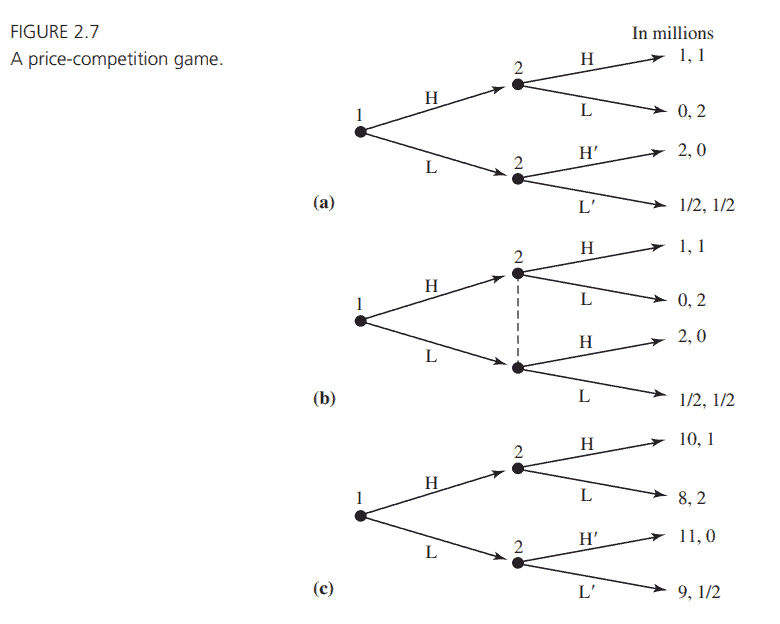
So that you get a bit more exposure to the extensive form, and so that I can register some technical notes, consider a few abstract examples of games. Figure 2.7(a) depicts a simple market game, where two firms compete by each selecting either a high $(\mathrm{H})$ or low $(\mathrm{L})$ price for a product that they both produce. Note that I have labeled the decision nodes with the player numbers; that is, firm 1 moves first, followed by firm 2. It is often useful to refer to players by number. Then, when we wish to speak of a generic player, we can use the phrase “player $i$,” where $i$ stands for any one of the player numbers; that is, in a game with $n$ players, $i=1,2, \ldots, n$. Remember to use the convention of listing the players’ payoffs in the order of the players’ identifying numbers. In general, player 1’s payoff is written first, followed by player 2’s payoff, and so on.
Observe that in Figure 2.7(a) I have used different action labels to describe firm 2’s high and low price options in this firm’s two information sets (the top and bottom nodes). This helps us avoid ambiguous statements such as, “Firm 2 chose a high price.” In fact, firm 2 has two decisions to make in this game, one at its top node and another at its bottom node. By following the labeling convention, we are correctly forced to say, “Firm 2 chose a high price at its top information set” (action H) or “Firm 2 chose a high price at its bottom information set” (action $\left.\mathrm{H}^{\prime}\right)$.
Figure 2.7(b) depicts a game in which the firms select their prices simultaneously and independently, so neither firm observes the other’s move before making its choice. In an extensive form, we must draw one player’s decision before that of the other, but it is important to realize that this does not necessarily correspond to the actual timing of the strategic setting. In this example, the moves are simultaneous. The key to modeling simultaneous choice in the extensive form is to get the information sets right. Because firm 2 moves at the same time as does firm 1, firm 2 does not get to observe firm l’s selection before making its own choice. Thus, firm 2 cannot distinguish between its two decision nodes-they are in the same information set and therefore connected with a dashed line. To check your understanding, you might see how one can draw the extensive form in Figure 2.7(b) so that firm 2’s action occurs at the initial node, followed by firm 1’s decision. However the game is drawn, each firm has just one decision to make.

博弈论代写

经济代写|博弈论代考Game theory代写|The Meaning of “Game”

在我们开始讨论这个理论之前，有必要先说明一下冲突与合作。大多数体育和休闲游戏都被认为是对抗性比赛(有人赢，有人输)。然而，正如已经指出的那样，许多相互依存的环境并不完全符合这一类别。事实上，大多数情况既包含冲突因素，也包含潜在的合作或协调因素，或两者兼而有之。假设有一家公司，两位经理共同开发一种新产品。他们的个人行为可能会影响彼此从项目中获得的回报，因此设置涉及相互依赖。但必须有赢家和输家吗?人们当然可以想象双方经理人在某种程度上“赢”或“输”的结果。也许如果经理们在开发产品时相互合作，双方都有可能从项目的成功中获益。另一方面，每个管理者可能都有动机提供比另一方更少的努力。再举一个既有冲突又有合作的例子，考虑一个工人和他的雇主之间的合同问题。他们可能需要在生产经济产品之前就工资合同进行谈判。虽然双方的利益可能会在工人工资问题上发生冲突，但他们的利益可能会在另一个维度上更加一致。例如，双方可能都希望合同中包括工人在工作中表现出色时获得的奖金，因为奖金可能会给工人创造利润的正确激励，他们可以分享利润。你可能认识到，这种“集中精力把蛋糕做大”的主题，是一些关于讨价还价的管理学书籍的主题。尽管如此，这是一个很好的例子，说明在许多情况下，冲突与合作是如何同时出现的。考虑到冲突和合作是重叠的，我将从更广泛的角度来看待游戏的构成。简而言之，游戏是对战略设置的正式描述。因此，博弈论是一种正式研究相互依存情况的方法。我所说的“形式上”是指使用数学上精确且逻辑上一致的结构。有了正确的理论工具，我们就可以在各种情况下研究行为，从而更好地理解经济，更广泛地说，理解社会互动

经济代写|博弈论代考Game theory代写|Other Examples and Conventions

这样你们就能更深入地了解这个广泛的形式，这样我就可以记录一些技术注释，考虑一些游戏的抽象例子。图2.7(a)描述了一个简单的市场博弈，其中两家公司通过各自选择高$(\ mathm {H})$或低$(\ mathm {L})$的价格来竞争各自生产的产品。注意，我已经用玩家编号标记了决策节点;也就是说，公司1先行动，然后是公司2。用数字来指代球员通常是有用的。然后，当我们希望谈论一般玩家时，我们可以使用短语“玩家$i$”，其中$i$代表任何一个玩家号码;也就是说，在一个有$n$玩家的博弈中，$i=1,2， $ ldots, n$。记住要按照玩家识别号码的顺序列出玩家的收益。一般来说，参与人1的收益先写，然后是参与人2的收益，以此类推。
注意，在图2.7(a)中，我使用了不同的动作标签来描述公司2在该公司的两个信息集(顶部和底部节点)中的高价和低价选项。这有助于我们避免模棱两可的陈述，如“公司2选择了高价格”。事实上，公司2在这个博弈中有两个决策，一个在它的顶部节点，另一个在它的底部节点。通过遵循标记约定，我们正确地被迫说，“公司2在其顶部信息集选择了高价格”(动作H)或“公司2在其底部信息集选择了高价格”(动作$\left.\ mathm {H}^{\prime}\right)$。
图2.7(b)描述了一个博弈，在这个博弈中，两家公司同时独立地选择价格，因此在做出选择之前，两家公司都不会观察对方的行动。在广泛的形式中，我们必须在另一个玩家之前绘制一个玩家的决定，但重要的是要意识到这并不一定与战略设置的实际时间相对应。在这个例子中，移动是同步的。同时选择泛化建模的关键是获取正确的信息集。因为公司2和公司1同时移动，公司2在做出自己的选择之前不能观察到公司1的选择。因此，公司2不能区分它的两个决策节点——它们在相同的信息集中，因此用虚线连接。为了检查您的理解，您可能会看到如何绘制图2.7(b)中的扩展形式，以便公司2的动作发生在初始节点，然后是公司1的决策。无论胜负如何，每家公司都只有一个决定。

经济代写|博弈论代考Game theory代写 请认准exambang™. exambang™为您的留学生涯保驾护航。

微观经济学代写

微观经济学是主流经济学的一个分支，研究个人和企业在做出有关稀缺资源分配的决策时的行为以及这些个人和企业之间的相互作用。my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数学Mathematics代写服务。我们的专家在图论代写Graph Theory代写方面经验极为丰富，各种图论代写Graph Theory相关的作业也就用不着 说。

线性代数代写

线性代数是数学的一个分支，涉及线性方程，如：线性图，如：以及它们在向量空间和通过矩阵的表示。线性代数是几乎所有数学领域的核心。

博弈论代写

现代博弈论始于约翰-冯-诺伊曼（John von Neumann）提出的两人零和博弈中的混合策略均衡的观点及其证明。冯-诺依曼的原始证明使用了关于连续映射到紧凑凸集的布劳威尔定点定理，这成为博弈论和数学经济学的标准方法。在他的论文之后，1944年，他与奥斯卡-莫根斯特恩（Oskar Morgenstern）共同撰写了《游戏和经济行为理论》一书，该书考虑了几个参与者的合作游戏。这本书的第二版提供了预期效用的公理理论，使数理统计学家和经济学家能够处理不确定性下的决策。

微积分代写

微积分，最初被称为无穷小微积分或 “无穷小的微积分”，是对连续变化的数学研究，就像几何学是对形状的研究，而代数是对算术运算的概括研究一样。

它有两个主要分支，微分和积分；微分涉及瞬时变化率和曲线的斜率，而积分涉及数量的累积，以及曲线下或曲线之间的面积。这两个分支通过微积分的基本定理相互联系，它们利用了无限序列和无限级数收敛到一个明确定义的极限的基本概念 。

计量经济学代写

什么是计量经济学？
计量经济学是统计学和数学模型的定量应用，使用数据来发展理论或测试经济学中的现有假设，并根据历史数据预测未来趋势。它对现实世界的数据进行统计试验，然后将结果与被测试的理论进行比较和对比。

根据你是对测试现有理论感兴趣，还是对利用现有数据在这些观察的基础上提出新的假设感兴趣，计量经济学可以细分为两大类：理论和应用。那些经常从事这种实践的人通常被称为计量经济学家。

Matlab代写

MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中，其中问题和解决方案以熟悉的数学符号表示。典型用途包括：数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发，包括图形用户界面构建MATLAB 是一个交互式系统，其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题，尤其是那些具有矩阵和向量公式的问题，而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问，这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展，得到了许多用户的投入。在大学环境中，它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域，MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要，工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数（M 文件）的综合集合，可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。