MY-ASSIGNMENTEXPERT™可以为您提供 sydney STAT4025 Time series analysis时间序列分析的代写代考和辅导服务!
这是悉尼大学 时间序列分析的代写成功案例。
STAT4025课程简介
This unit will study basic concepts and methods of time series analysis applicable in many real world problems in numerous fields, including economics, finance, insurance, physics, ecology, chemistry, computer science and engineering. This unit will investigate the basic methods of modelling and analyzing of time series data (i.e. data containing serially dependence structure). This can be achieved through learning standard time series procedures on identification of components, autocorrelations, partial autocorrelations and their sampling properties. After setting up these basics, students will learn the theory of stationary univariate time series models including ARMA, ARIMA and SARIMA and their properties. Then the identification, estimation, diagnostic model checking, decision making and forecasting methods based on these models will be developed with applications. The spectral theory of time series, estimation of spectra using periodogram and consistent estimation of spectra using lag-windows will be studied in detail. Further, the methods of analyzing long memory and time series and heteroscedastic time series models including ARCH, GARCH, ACD, SCD and SV models from financial econometrics and the analysis of vector ARIMA models will be developed with applications. By completing this unit, students will develop the essential basis for further studies, such as financial econometrics and financial time series. The skills gained through this unit of study will form a strong foundation to work in a financial industry or in a related research organization.
Prerequisites
At the completion of this unit, you should be able to:
- LO1. 1. Explain and examine time series data and Identify components of a time series; remove trends, seasonal and other components.
- LO2. Identify stationarity time series; sample autocorrelations and partial autocorrelations, probability models for stationary time series.
- LO3. Explain homogeneous nonstationary time series, simple and integrated models and related results.
- LO4. Apply estimation and fitting methods for ARIMA models via MM and MLE methods. Apply hypothesis testing, diagnostic checking and goodness-of-fit tests
- LO5. Apply hypothesis testing, diagnostic checking and goodness-of-fit tests methodology.
- LO6. Construct forecasting methods for ARIMA models.
- LO7. Explain spectral methods in time series analysis
- LO8. Apply financial time series and related models to straightforward problems.
- LO9. Apply the methods of analysis of GARCH and other models for volatility.
- LO10. Explain and apply methods of vector time series models
STAT4025 Time series analysis HELP(EXAM HELP, ONLINE TUTOR)
Which of these sequences can used as the autocovariance function of a second order stationary time series?
(i) $c(-1)=1 / 2, c(0)=1, c(1)=1 / 2$ and for all $|k|>1, c(k)=0$.
(ii) $c(-1)=-1 / 2, c(0)=1, c(1)=1 / 2$ and for all $|k|>1, c(k)=0$.
(iii) $c(-2)=-0.8, c(-1)=0.5, c(0)=1, c(1)=0.5$ and $c(2)=-0.8$ and for all $|k|>2$, $c(k)=0$.
(i) Show that the function $c(u)=\exp (-a|u|)$ where $a>0$ is a positive semidefinite function.
(ii) Show that the commonly used exponential spatial covariance defined on $\mathbb{R}^2, c\left(u_1, u_2\right)=$ $\exp \left(-a \sqrt{u_1^2+u_2^2}\right)$, where $a>0$, is a positive semi-definite function.
Hint: One method is to make a change of variables using Polar coordinates. You may also want to harness the power of Mathematica or other such tools.
State, with explanation, which of the following time series is second order stationary, which are strictly stationary and which are both.
(i) $\left{\varepsilon_t\right}$ are iid random variables with mean zero and variance one.
(ii) $\left{\varepsilon_t\right}$ are iid random variables from a Cauchy distributon.
(iii) $X_{t+1}=X_t+\varepsilon_t$, where $\left{\varepsilon_t\right}$ are iid random variables with mean zero and variance one.
(iv) $X_t=Y$ where $Y$ is a random variable with mean zero and variance one.
(iv) $X_t=U_t+U_{t-1}+V_t$, where $\left{\left(U_t, V_t\right)\right}$ is a strictly stationary vector time series with $\mathrm{E}\left[U_t^2\right]<\infty$ and $\mathrm{E}\left[V_t^2\right]<\infty$.
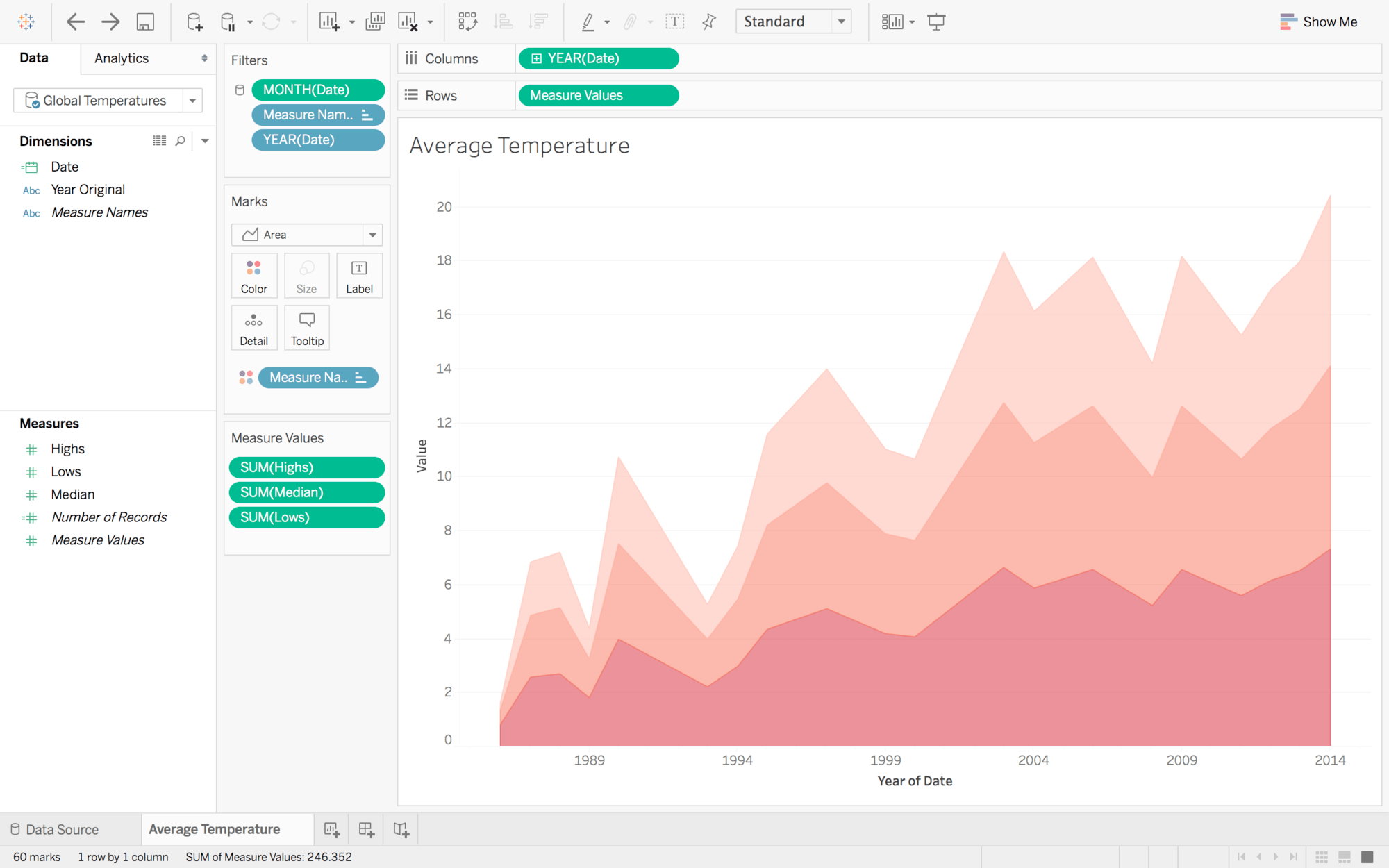
(i) Make an ACF plot of the monthly temperature data from 1996-2014.
(ii) Make and ACF plot of the yearly temperature data from 1880-2013.
(iii) Make and ACF plot of the residuals (after fitting a line through the data (using the command lsfit (.. \$res)) of the yearly temperature data from 1880-2013.
Briefly describe what you see.
(i) Suppose that $\left{X_t\right}_t$ is a strictly stationary time series. Let
$$
Y_t=\frac{1}{1+X_t^2} .
$$
Show that $\left{Y_t\right}$ is a second order stationary time series.
(ii) Obtain an approximate expression for the variance of the sample mean of $\left{Y_t\right}$ in terms of its long run variance (stating the sufficient assumptions for the long run variance to be finite). You do not need to give an analytic expression for the autocovariance, there is not enough information in the question to do this.
(iii) Possibly challenging question. Suppose that
$$
Y_t=g\left(\theta_0, t\right)+\varepsilon_t,
$$
where $\left{\varepsilon_t\right}$ are iid random variables and $g\left(\theta_0, t\right)$ is a deterministic mean and $\theta_0$ is an unknown parameter. Let
$$
\widehat{\theta}n=\arg \min {\theta \in \Theta} \sum_{t=1}^n\left(Y_t-g(\theta, t)\right)^2 .
$$
Explain why the quantity
$$
\widehat{\theta}_n-\theta_0
$$
can be expressed, approximately, as a sample mean. You can use approximations and heuristics here.
Hint: Think derivatives and mean value theorems.
MY-ASSIGNMENTEXPERT™可以为您提供 sydney STAT4025 Time series analysis时间序列分析的代写代考和辅导服务!