如果你也在 怎样代写光学Optics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。光学Optics始于古埃及人和美索不达米亚人对镜片的开发。最早的已知透镜由抛光的水晶制成,通常是石英,最早可追溯到公元前2000年的克里特岛(希腊赫拉克里翁考古博物馆)。罗德岛的镜片可追溯到公元前700年左右,亚述人的镜片也是如此,如尼姆鲁德的镜片。古代罗马人和希腊人将玻璃球装满水来制作透镜。在这些实践发展之后,古希腊和印度的哲学家们发展了关于光和视觉的理论,并在希腊-罗马世界中发展了几何光学。光学这个词来自古希腊词ὀπτική(optikē),意思是 “外观,看”。
光学Optics是研究光的行为和属性的物理学分支,包括它与物质的相互作用以及使用或探测它的仪器的构造。光学通常描述可见光、紫外光和红外光的行为。
my-assignmentexpert™ 光学Optics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的光学Optics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此光学Optics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在物理physics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理physics代写服务。我们的专家在光学Optics代写方面经验极为丰富,各种光学Optics相关的作业也就用不着 说。
我们提供的光学Optics及其相关学科的代写,服务范围广, 其中包括但不限于:
- 几何光学 Geometrical optics
几何光学,或称射线光学,是一种用射线来描述光的传播的光学模型。几何光学中的射线是一个抽象的概念,有助于近似地描述光线在某些情况下的传播路径。
- 波动光学
在物理学中,波动光学,或称波光学,是光学的一个分支,研究干涉、衍射、偏振和其他几何光学中的射线近似不成立的现象。
- 量子光学
量子光学是原子、分子和光学物理学的一个分支,处理单个光量子(称为光子)如何与原子和分子互动的问题。它包括研究光子的类似粒子的特性。

物理代写|光学作业代写Optics代考|Pure states of polarization
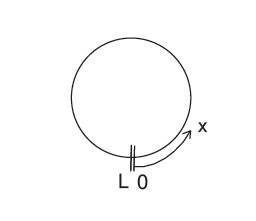
Although the conventional definition of the correlation function – see Eq.13 of Brunner et al. [23] – involves the same state of polarization reaching the two separate detectors, in the case of quantum Rayleigh spontaneous emission additional correlations can be defined between different states of polarization – possibly boosting the detection counts – for two different angles $\varphi_{1}$ and $\varphi_{2}$, relative to the $x$-axis of reference.
Correlation functions $E_{c}$ for a quantum behaviour are defined [23] as the expectation value of the tensor product of two measurement operators for a set of initial state vectors which are projected onto the measurement Hilbert space $\mathcal{H}{m}=\mathcal{H}{1} \otimes \mathcal{H}{2}$ in the expression $$ E{c}=\left\langle\Psi\left(\varphi_{1}\right)\left|\hat{p}\left(\theta_{1}\right) \otimes \hat{p}\left(\theta_{2}\right)\right| \Psi\left(\varphi_{2}\right)\right\rangle=\left\langle\Phi_{1}|\otimes| \Phi_{2}\right\rangle
$$
The second line of eq. (6) indicates that the projected states $|\Phi(\varphi)\rangle$ lie in the measurement space of $\mathcal{H}_{m}$ which identifies the comparison of measured values with a localized measurement [18].
The polarisation eigenstates of the measured photons, rotated by an angle $\theta_{j}$ from the reference or generic states $|x\rangle$ and $|y\rangle$ are denoted as
$$
\begin{aligned}
&\left|x\left(\theta_{j}\right)\right\rangle=\cos \theta_{j}|x\rangle+\sin \theta_{j}|y\rangle \
&\left|y\left(\theta_{j}\right)\right\rangle=-\sin \theta_{j}|x\rangle+\cos \theta_{j}|y\rangle
\end{aligned}
$$
and the quantum operator measuring polarisation properties of the photons is the projector
$$
\begin{aligned}
\hat{p}\left(\theta_{j}\right) &=\left|x\left(\theta_{j}\right)\right\rangle\left\langle x\left(\theta_{j}\right)|-| y\left(\theta_{j}\right)\right\rangle\left\langle y\left(\theta_{j}\right)\right|=\
&=\sin \left(2 \theta_{j}\right) \hat{\sigma}{1}+\cos \left(2 \theta{j}\right) \hat{\sigma}_{3}
\end{aligned}
$$
物理代写|光学作业代写OPTICS代考|The Heisenberg uncertainty of predicted values
The expectation values of the operator products $\hat{\sigma}{1} \hat{\sigma}{3}$ are found to vanish for pure states of eq. (7.5), i.e.,
$$
\begin{aligned}
&\left\langle\Psi(\varphi)\left|\hat{\sigma}{3} \hat{\sigma}{1}\right| \Psi(\varphi)\right\rangle=0 \
&\left\langle\Psi(\varphi)\left|\hat{\sigma}{1} \hat{\sigma}{3}\right| \Psi(\varphi)\right\rangle=0
\end{aligned}
$$
136
Chapter Seven
because $\hat{\sigma}{1} \hat{\sigma}{3}|\Psi(\varphi)\rangle=|\Psi(\varphi+\pi / 2)\rangle$. As a result, each term of the resulting commutative relation vanishes and we obtain
$$
\left\langle\Psi(\varphi)\left|\left[\hat{\sigma}{1}, \hat{\sigma}{3}\right]\right| \Psi(\varphi)\right\rangle=0
$$
for the lowest limit of uncertainty involving the two Pauli operators. The eigenstates of $\hat{\sigma}{1}$ are superpositions of the eigenvectors of $\hat{\sigma}{3}$ on the twodimensional Hilbert space $\mathcal{H}$ and simultaneous measurements of well-defined values are possible as their product operator $\hat{\sigma}{1} \hat{\sigma}{3}$ flips the eigenstates $|\Psi(\varphi)\rangle$ and $|\Psi(\varphi+\pi / 2)\rangle$ onto each other. Thus, the output value is indicative of the input one, and each term of the commutator vanishes for the wave functions $|\Psi(\varphi)\rangle$ of eq. (7.5) or eq. (7.6). Consequently, the simultaneous measurement of the two operators in the context of the single and independent qubit wave functions is capable of identifying the incoming state as well as the measured one.
物理代写|光学作业代写OPTICS代考|Mixed states of polarization
The overall correlation for one step of spontaneous emission will be found by adding up probability-weighted correlation functions of eq. (7.13) as the ensemble of polarisations states generated over a time interval corresponds to a mixed quantum state described by the density matrix elements
$$
\rho_{m n}(\varphi)=p(\varphi)\langle m \mid \Psi(\varphi)\rangle\langle\Psi(\varphi) \mid n\rangle
$$
where $m, n=x, y$. A possible probability density can be identified from eq. (7.4) above, that is,
Quantum Rayleigh Annihilation of Entangled Photons
137
$$
p(\varphi)=\frac{\cos ^{2} \varphi}{0.5 \pi}
$$
for generating the state $|\Psi(\varphi)\rangle$ over the range $\varphi \in{-\pi / 2, \pi / 2}$. This leads to a higher probability for the interval ${-\pi / 4, \pi / 4}$ than for the intervals ${-\pi / 2,-\pi / 4}$ and ${\pi / 4, \pi / 2}$.
The correlation function for the mixed state of an ensemble is evaluated similarly to eq. (7.13) after using the transformation
$$
|\Psi(\varphi)\rangle \rightarrow \sqrt{p(\varphi)}|\Psi(\varphi)\rangle
$$
in eq. (7.7) to obtain:
$E_{c}=\cos 2\left(\theta_{1}-\theta_{2}\right)+\int d \varphi_{2} \sqrt{p\left(\varphi_{2}\right)} \times$
$\times \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} d \varphi_{1} \sqrt{p\left(\varphi_{1}\right)} \cos \left[2\left(\theta_{1}-\theta_{2}\right)-\left(\varphi_{1}-\varphi_{2}\right)\right] \times$
$\times\left[1-\delta\left(\varphi_{1}-\varphi_{2}\right)\right]$
where the first term reproduces the result for identical and independent qubits, i.e., $\varphi_{1}=\varphi_{2}$, with $\delta$ being Dirac’s delta function. The second term of (7.16) depends on the polarization state distribution of the mixed state, providing the possibility of controlling the level of correlation with various distributions of polarizations.
物理代写
物理代写|光学作业代写OPTICS代考|PURE STATES OF POLARIZATION
虽然相关函数的传统定义——参见 Brunner 等人的 Eq.13。23– 涉及到达两个单独检测器的相同偏振状态,在量子瑞利自发发射的情况下,可以在不同的偏振状态之间定义额外的相关性 – 可能增加检测计数 – 对于两个不同的角度披1和披2, 相对于X-参考轴。
相关函数和C定义了一个量子行为23作为投影到测量希尔伯特空间上的一组初始状态向量的两个测量算子的张量积的期望值H米=H1⊗H2在表达式中和C=⟨Ψ(披1)|p^(θ1)⊗p^(θ2)|Ψ(披2)⟩=⟨披1|⊗|披2⟩
等式的第二行。6表示投影状态|披(披)⟩位于测量空间H米识别测量值与局部测量的比较18.
测量光子的偏振本征态,旋转一个角度θj从参考或通用状态|X⟩和|是⟩表示为
|X(θj)⟩=某物θj|X⟩+没有θj|是⟩ |是(θj)⟩=−没有θj|X⟩+某物θj|是⟩
测量光子偏振特性的量子算子是投影仪
p^(θj)=|X(θj)⟩⟨X(θj)|−|是(θj)⟩⟨是(θj)|= =没有(2θj)σ^1+某物(2θj)σ^3
物理代写|光学作业代写OPTICS代考|THE HEISENBERG UNCERTAINTY OF PREDICTED VALUES
运营商产品的期望值σ^1σ^3发现对于等式的纯状态消失。7.5, IE,
⟨Ψ(披)|σ^3σ^1|Ψ(披)⟩=0 ⟨Ψ(披)|σ^1σ^3|Ψ(披)⟩=0
136
第7章
因为σ^1σ^3|Ψ(披)⟩=|Ψ(披+圆周率/2)⟩. 结果,得到的交换关系的每一项都消失了,我们得到
⟨Ψ(披)|[σ^1,σ^3]|Ψ(披)⟩=0
对于涉及两个泡利算子的不确定性的最低限度。的本征态σ^1是特征向量的叠加σ^3在二维希尔伯特空间上H作为产品操作员,可以同时测量明确定义的值σ^1σ^3翻转本征态|Ψ(披)⟩和|Ψ(披+圆周率/2)⟩彼此身上。因此,输出值表示输入值,并且换向器的每一项对于波函数都消失了|Ψ(披)⟩当量7.5或等式。7.6. 因此,在单个和独立的量子比特波函数的上下文中同时测量两个算子能够识别输入状态以及测量的状态。
物理代写|光学作业代写OPTICS代考|MIXED STATES OF POLARIZATION
通过将方程的概率加权相关函数相加,将找到一步自发发射的整体相关性。7.13因为在一个时间间隔内产生的极化状态集合对应于由密度矩阵元素描述的混合量子状态
ρ米n(披)=p(披)⟨米∣Ψ(披)⟩⟨Ψ(披)∣n⟩
在哪里米,n=X,是. 一个可能的概率密度可以从等式中确定。7.4上图,即
纠缠光子的量子瑞利湮灭
137
p(披)=某物2披0.5圆周率
用于生成状态|Ψ(披)⟩在范围内披∈−圆周率/2,圆周率/2. 这导致间隔的概率更高−圆周率/4,圆周率/4比间隔−圆周率/2,−圆周率/4和圆周率/4,圆周率/2.
集成混合状态的相关函数的评估与等式类似。7.13使用转换后
|Ψ(披)⟩→p(披)|Ψ(披)⟩
在等式。7.7获得:
和C=某物2(θ1−θ2)+∫d披2p(披2)×
×∫−圆周率2圆周率2d披1p(披1)某物[2(θ1−θ2)−(披1−披2)]×
×[1−d(披1−披2)]
其中第一项再现相同和独立量子位的结果,即披1=披2, 和d是狄拉克的δ函数。第二届7.16取决于混合态的偏振态分布,提供了控制与各种偏振分布的相关水平的可能性。

物理代写|光学作业代写Optics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。