如果你也在 怎样代写matlab这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。matlab是由MathWorks公司开发的一种专有的多范式编程语言和数字计算环境。MATLAB允许进行矩阵操作、绘制函数和数据、实现算法、创建用户界面以及与用其他语言编写的程序对接。
matlab尽管MATLAB主要用于数值计算,但一个可选的工具箱使用MuPAD符号引擎,允许访问符号计算能力。一个额外的软件包,Simulink,为动态和嵌入式系统增加了图形化的多域仿真和基于模型的设计。截至2020年,MATLAB在全球拥有超过400万用户。他们来自工程、科学和经济的各种背景。
my-assignmentexpert™ matlab作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的matlab作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此matlab作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的matlab代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种matlab相关的作业也就用不着 说。
我们提供的matlab及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|matlab代写|Introduction
In two-point boundary value problems the auxiliary conditions associated with the differential equation, called the boundary conditions, are specified at two different values of $x$. This seemingly small departure from initial value problems has a major repercussion-it makes boundary value problemsconsiderably more difficult to solve. In an initial value problem we were able to start at the point where the initial values were given and march the solution forward as far as needed. This technique does not work for boundary value problems, because there are not enough starting conditions available at either end point to produce a unique solution.
One way to overcome the lack of starting conditions is to guess the missing values. The resulting solution is very unlikely to satisfy boundary conditions at the other end, but by inspecting the discrepancy we can estimate what changes to make to the initial conditions before integrating again. This iterative procedure is known as the shooting method. The name is derived from analogy with target shooting – take a shot and observe where it hits the target, then correct the aim and shoot again.
Another means of solving two-point boundary value problems is the finite difference method, where the differential equations are approximated by finite differences at evenly spaced mesh points. As a consequence, a differential equation is transformed into set of simultaneous algebraic equations.
The two methods have a common problem: they give rise to nonlinear sets of equationsif the differential equation is not linear. As we noted in Chapter 4 , all methods of solving nonlinear equations are iterative procedures that cansume a lot of computational resources. Thus solution of nonlinear boundary value problems is not cheap. Another complication is that iterative methods need reasonably good starting values in order to converge. Since there is no set formula for determining these, an algorithm for solving nonlinear boundary value problems requires intelligent input; it cannot be treated as a “black box.”
数学代写|matlab代写|Shooting Method
The simplest two-point boundary value problem is a second-order differential equation with one condition specified at $x=a$ and another one at $x=b$. Here is an example of a second-order boundary value problem:
$$
y^{\prime \prime}=f\left(x, y, y^{\prime}\right), \quad y(a)=\alpha, \quad y(b)=\beta
$$
Let us now attempt to turn Eqs. (8.1) into the initial value problem
$$
y^{\prime \prime}=f\left(x, y, y^{\prime}\right), \quad y(a)=\alpha, \quad y^{\prime}(a)=u
$$
The key to success is finding the correct value of $u$. This could be done by trial and error: guess $u$ and solve the initial value problem by marching from $x=a$ to $b$. If the solution agrees with the prescribed boundary condition $y(b)=\beta$, we are done; otherwise we have to adjust $u$ and try again. Clearly, this procedure is very tedious.
More systematic methods become available to us if we realize that the determination of $u$ is a root-finding problem. Because the solution of the initial value problem depends on $u$, the computed boundary value $y(b)$ is a function of $u$; that is
$$
y(b)=\theta(u)
$$
Hence $u$ is a root of
$$
r(u)=\theta(u)-\beta=0
$$
where $r(u)$ is the boundary residual (difference between the computed and specified boundary values). Equation (8.3) can be solved by any one of the root-finding methods discussed in Chapter 4. We reject the method of bisection because it involves too many evaluations of $\theta(u)$. In the Newton-Raphson method we run into the problem of having to compute $d \theta / d u$, which can be done, but not easily. That leaves Brent’s algorithm as our method of choice.
Here is the procedure we use in solving nonlinear boundary value problems:
- Specify the starting values $u_{1}$ and $u_{2}$ which must bracket the root $u$ of Eq. (8.3).
- Apply Brent’s method to solve Eq. (8.3) for $u$. Note that each iteration requires evaluation of $\theta(u)$ by solving the differential equation as an initial value problem.
- Having determined the value of $u$, solve the differential equations once more and record the results.
If the differential equation is linear, any root-finding method will need only one interpolation to determine $u$. But since Brent’s method uses quadratic interpolation, it needs three points: $u_{1}, u_{2}$ and $u_{3}$, the latter being provided by a bisection step. This is wasteful, since linear interpolation with $u_{1}$ and $u_{2}$ would also result in the correct value of $u$. Therefore, we replace Brent’s method with linear interpolation whenever the differential equation is linear.
数学代写|MATLAB代写|Finite Difference Method
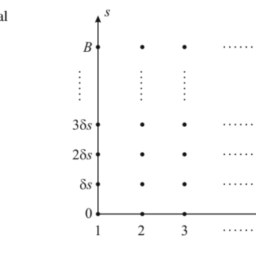
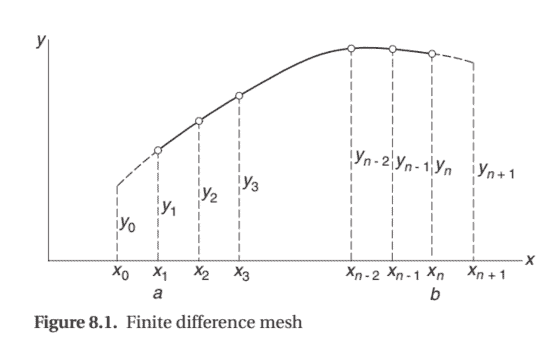
In the finite difference method we divide the range of integration $(a, b)$ into $n-1$ equal subintervals of length $h$ each, as shown in Fig. 8.1. The values of the numerical solution at the mesh points are denoted by $y_{i}, i=1,2 \ldots, n$; the two points outside $(a, b)$ will be explained shortly. We then make two approximations:
- The derivatives of $y$ in the differential equation are replaced by the finite difference expressions. It is common practice to use the first central difference approximations (see Chapter 5):
$$
y_{i}^{\prime}=\frac{y_{i+1}-y_{i-1}}{2 h} \quad y_{i}^{\prime \prime}=\frac{y_{i-1}-2 y_{i}+y_{i+1}}{h^{2}} \quad \text { etc. }
$$ - The differential equation is enforced only at the mesh points.
As a result, the differential equations are replaced by $n$ simultaneous algebraic equations, the unknowns being $y_{i}, i=1,2, \ldots n$. If the differential equation is nonlinear, the algebraic equations will also be nonlinear and must be solved by the NewtonRaphson method.
Since the truncation error in a first central difference approximation is $\mathcal{O}\left(h^{2}\right)$, the finite difference method is not as accurate as the shooting method-recall that the Runge-Kutta method has a truncation error of $O\left(h^{5}\right)$. Therefore, the convergence criterion in the Newton-Raphson method should not be too severe.
matlab代写
数学代写|MATLAB代写|INTRODUCTION
在两点边界值问题中,与微分方程相关的辅助条件,称为边界条件,指定为两个不同的值X. 这种与初值问题看似很小的偏差却产生了重大影响——它使边值问题的解决变得相当困难。在初始值问题中,我们能够从给定初始值的点开始,并根据需要推进解决方案。此技术不适用于边界值问题,因为在任一端点都没有足够的起始条件来产生唯一的解决方案。
克服缺乏起始条件的一种方法是猜测缺失值。得到的解决方案不太可能满足另一端的边界条件,但通过检查差异,我们可以估计在再次积分之前对初始条件进行哪些更改。这种迭代过程被称为拍摄方法。这个名字来源于与目标射击的类比——射击并观察它击中目标的位置,然后纠正目标并再次射击。
解决两点边值问题的另一种方法是有限差分法,其中微分方程通过均匀间隔网格点的有限差分来近似。结果,微分方程被转换为联立代数方程组。
这两种方法有一个共同的问题:如果微分方程不是线性的,它们会产生非线性方程组。正如我们在第 4 章中提到的,所有求解非线性方程的方法都是迭代过程,会消耗大量计算资源。因此非线性边值问题的求解并不便宜。另一个复杂因素是迭代方法需要相当好的起始值才能收敛。由于没有确定这些的固定公式,解决非线性边值问题的算法需要智能输入;它不能被视为“黑匣子”。
数学代写|MATLAB代写|SHOOTING METHOD
最简单的两点边值问题是一个二阶微分方程,其中一个条件指定为X=一种另一个在X=b. 下面是一个二阶边值问题的例子:
是′′=F(X,是,是′),是(一种)=一种,是(b)=b
现在让我们尝试转动方程式。8.1进入初值问题
是′′=F(X,是,是′),是(一种)=一种,是′(一种)=在
成功的关键是找到正确的价值在. 这可以通过反复试验来完成:guess在并通过从X=一种到b. 如果解符合规定的边界条件是(b)=b, 我们完了; 否则我们必须调整在然后再试一次。显然,这个过程非常繁琐。
如果我们意识到确定在是一个寻根问题。因为初值问题的解取决于在, 计算的边界值是(b)是一个函数在; 那是
是(b)=θ(在)
因此在是一个根
r(在)=θ(在)−b=0
在哪里r(在)是边界残差d一世FF和r和nC和b和吨在和和n吨H和C这米p在吨和d一种ndsp和C一世F一世和db这在nd一种r是在一种l在和s. 方程8.3可以通过第 4 章中讨论的任何一种求根方法来解决。我们拒绝二分法,因为它涉及太多的评估θ(在). 在 Newton-Raphson 方法中,我们遇到了必须计算的问题dθ/d在,这可以做到,但并不容易。这使得布伦特算法成为我们选择的方法。
以下是我们用于解决非线性边值问题的程序:
- 指定起始值在1和在2必须将根括起来在方程。8.3.
- 应用布伦特方法求解方程。8.3为了在. 请注意,每次迭代都需要评估θ(在)通过求解微分方程作为初值问题。
- 确定了价值在,再次求解微分方程并记录结果。
如果微分方程是线性的,任何求根方法都只需要一次插值来确定在. 但由于布伦特的方法使用二次插值,它需要三点:在1,在2和在3,后者由二等分步骤提供。这是浪费的,因为线性插值在1和在2也会导致正确的值在. 因此,只要微分方程是线性的,我们就用线性插值代替布伦特方法。
数学代写|MATLAB代写|FINITE DIFFERENCE METHOD
在有限差分法中,我们划分积分范围(一种,b)进入n−1长度相等的子区间H如图 8.1 所示。网格点处数值解的值表示为是一世,一世=1,2…,n; 外面的两点(一种,b)将很快解释。然后我们做两个近似:
- 的衍生物是用有限差分表达式代替微分方程中的。通常的做法是使用第一中心差分近似s和和CH一种p吨和r5:
是一世′=是一世+1−是一世−12H是一世′′=是一世−1−2是一世+是一世+1H2 等等 - 微分方程仅在网格点处执行。
结果,微分方程被替换为n联立代数方程,未知数为是一世,一世=1,2,…n. 如果微分方程是非线性的,那么代数方程也将是非线性的,必须用 NewtonRaphson 方法求解。
由于第一中心差分近似中的截断误差为这(H2),有限差分法不如射击法准确——回想一下龙格-库塔法的截断误差为这(H5). 因此,Newton-Raphson 方法中的收敛准则不应太严格。

数学代写|matlab代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。