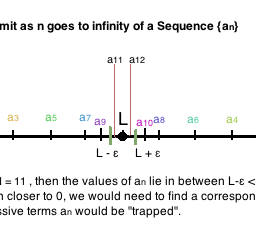
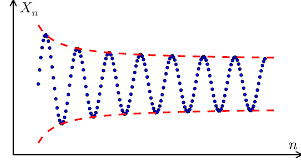
微积分note Sequences

Functions defined on the set of integers larger than a given integer are called sequences.
Definition 4.2.1 A function whose domain is defined as a set of the form
$$
{k, k+1, k+2, \cdots}
$$
for $k$ an integer is known as a sequence. Thus you can consider $f(k), f(k+1), f(k+2)$, etc. Usually the domain of the sequence is either $\mathbb{N}$, the natural numbers consisting of ${1,2,3, \cdots}$ or the nonnegative integers, ${0,1,2,3, \cdots}$. Also, it is traditional to write $f_{1}, f_{2}$, etc. instead of $f(1), f(2), f(3)$ etc. when referring to sequences. In the above context, $f_{k}$ is called the first term, $f_{k+1}$ the second and so forth. It is also common to write the sequence, not as $f$ but as $\left{f_{i}\right}_{i=k}^{\infty}$ or just $\left{f_{i}\right}$ for short.
Example 4.2.2 Let $\left{a_{k}\right}_{k=1}^{\infty}$ be defined by $a_{k} \equiv k^{2}+1$.
This gives a sequence. In fact, $a_{7}=a(7)=7^{2}+1=50$ just from using the formula for the $k^{t h}$ term of the sequence.

It is nice when sequences come in this way from a formula for the $k^{t h}$ term. However, this is often not the case. Sometimes sequences are defined recursively. This happens, when the first several terms of the sequence are given and then a rule is specified which determines $a_{n+1}$ from knowledge of $a_{1}, \cdots, a_{n}$. This rule which specifies $a_{n+1}$ from knowledge of $a_{k}$ for $k \leq n$ is known as a recurrence relation.

Example 4.2.3 Let $a_{1}=1$ and $a_{2}=1$. Assuming $a_{1}, \cdots, a_{n+1}$ are known, $a_{n+2} \equiv$ $a_{n}+a_{n+1}$.

Thus the first several terms of this sequence, listed in order, are $1,1,2,3,5,8, \cdots$. This particular sequence is called the Fibonacci sequence and is important in the study of reproducing rabbits. Note this defines a function without giving a formula for it. Such sequences occur naturally in the solution of differential equations using power series methods and in many other situations of great importance.
For sequences, it is very important to consider something called a subsequence.
Definition 4.2.4 Let $\left{a_{n}\right}$ be a sequence and let $n_{1}<n_{2}<n_{3}, \cdots$ be any strictly increasing list of integers such that $n_{1}$ is at least as large as the first number in the domain of the function. Then if $b_{k} \equiv a_{n_{k}},\left{b_{k}\right}$ is called a subsequence of $\left{a_{n}\right}$. Here $a_{n}$ is in some given set.

For example, suppose $a_{n}=\left(n^{2}+1\right)$. Thus $a_{1}=2, a_{3}=10$, etc. If $n_{1}=1, n_{2}=$ $3, n_{3}=5, \cdots, n_{k}=2 k-1$, then letting $b_{k}=a_{n_{k}}$, it follows
$$
b_{k}=\left((2 k-1)^{2}+1\right)=4 k^{2}-4 k+2 .
$$

在大于给定整数的整数集合上定义的函数称为序列。
定义 4.2.1 定义域为一组形式的函数
$$
{k, k+1, k+2, \cdots}
$$
对于$k$，整数称为序列。因此可以考虑 $f(k)、f(k+1)、f(k+2)$ 等。通常序列的域是 $\mathbb{N}$，由 $\ 组成的自然数{1,2,3, \cdots}$ 或非负整数 ${0,1,2,3, \cdots}$。此外，在提到序列时，传统上写成 $f_{1}、f_{2}$ 等而不是 $f(1)、f(2)、f(3)$ 等。在上述上下文中，$f_{k}$ 称为第一项，$f_{k+1}$ 称为第二项，依此类推。写序列也很常见，不是写成 $f$，而是写成 $\left{f_{i}\right}_{i=k}^{\infty}$ 或只是 $\left{f_{ i}\right}$ 简称。
例 4.2.2 令 $\left{a_{k}\right}_{k=1}^{\infty}$ 定义为 $a_{k} \equiv k^{2}+1$。
这给出了一个序列。实际上，$a_{7}=a(7)=7^{2}+1=50$ 只是使用序列的 $k^{th}$ 项的公式。

如果序列以这种方式来自 $k^{th}$ 项的公式，那就太好了。然而，情况往往并非如此。有时序列是递归定义的。当给出序列的前几个项，然后指定一个规则，该规则根据 $a_{1}、\cdots、a_{n}$ 的知识确定 $a_{n+1}$ 时，就会发生这种情况。这个从 $a_{k}$ 的知识中为 $k \leq n$ 指定 $a_{n+1}$ 的规则称为递归关系。

例 4.2.3 令 $a_{1}=1$ 和 $a_{2}=1$。假设 $a_{1}, \cdots, a_{n+1}$ 是已知的，$a_{n+2} \equiv$ $a_{n}+a_{n+1}$。

因此，这个序列的前几个项，按顺序列出，是 $1,1,2,3,5,8,\cdots$。这个特殊的序列被称为斐波那契序列，在兔子的繁殖研究中很重要。请注意，这定义了一个函数，但没有给出公式。这样的序列自然地出现在使用幂级数方法的微分方程的解中以及许多其他非常重要的情况中。
对于序列，考虑称为子序列的东西非常重要。
定义 4.2.4 令 $\left{a_{n}\right}$ 是一个序列并且令 $n_{1}<n_{2}<n_{3}, \cdots$ 是任何严格递增的整数列表使得 $n_{1}$ 至少与函数域中的第一个数字一样大。那么如果 $b_{k} \equiv a_{n_{k}},\left{b_{k}\right}$ 称为 $\left{a_{n}\right}$ 的子序列。这里 $a_{n}$ 在某个给定的集合中。

例如，假设 $a_{n}=\left(n^{2}+1\right)$。因此 $a_{1}=2, a_{3}=10$, 等等。如果 $n_{1}=1, n_{2}=$ $3, n_{3}=5, \cdots, n_{k} =2 k-1$，然后令$b_{k}=a_{n_{k}}$，如下
$$
b_{k}=\left((2 k-1)^{2}+1\right)=4 k^{2}-4 k+2 。
$$