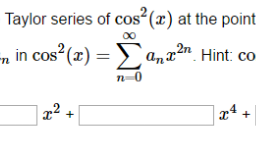0 0

By admin 数学代写 2022年2月23日

In this section, functions will be defined on some subset of $\mathbb{R}$ having values in $\mathbb{F}$. The restriction requiring $\mathbb{R}$ is because we want to consider one sided limits.

Definition 7.1.1 Let $f$ be a function which is defined on $D(f)$ where $D(f) \supseteq$ $(x-r, x) \cup(x, x+r)$ for some $r>0 .$ Note that $f$ is not necessarily defined at $x$. Then $\lim {y \rightarrow x} f(y)=L$ if and only if the following condition holds. For all $\varepsilon>0$ there exists $\delta>0$ such that if $$ 0<|y-x|<\delta, $$ then, $$ |L-f(y)|<\varepsilon \text {. } $$ If everything is the same as the above, except $y$ is required to be larger than $x$ and $f$ is only required to be defined on $(x, x+r)$, then the notation is $$ \lim {y \rightarrow x+} f(y)=L \text {. }
$$
If $f$ is only required to be defined on $(x-r, x)$ and $y$ is required to be less than $x$, with the same conditions above, we write
$$
\lim {y \rightarrow x-} f(y)=L \text {. } $$ Limits are also taken as a variable “approaches” infinity. Of course nothing is “close” to infinity and so this requires a slightly different definition. $$ \lim {x \rightarrow \infty} f(x)=L
$$
if for every $\varepsilon>0$ there exists $l$ such that whenever $x>l$,
$$
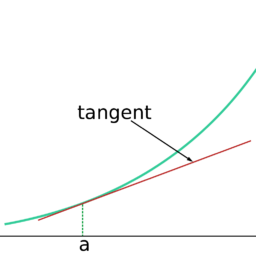
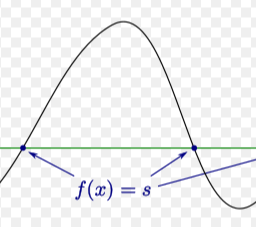
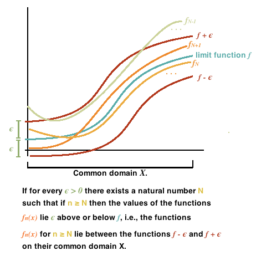
|f(x)-L|<\varepsilon $$ CHAPTER 7. THE DERIVATIVE 123 $\lim {x \rightarrow-\infty} f(x)=L$ In the left picture is shown the graph of a function. Note the value of the function at $x$ equals $c$ while $\lim {y \rightarrow x+} f(y)=b$ and $\lim {y \rightarrow x-} f(y)=a$. In the second picture, $\lim {y \rightarrow x} f(y)=b$. Note that the value of the function at the point $x$ has nothing to do with the limit of the function in any of these cases. The value of a function at $x$ is irrelevant to the value of the limit at $x !$ This must always be kept in mind. You do not evaluate interesting limits by computing $f(x) !$ In the above picture, $f(x)$ is always wrong! It may be the case that $f(x)$ is right but this is merely a happy coincidence when it occurs and as explained below in Theorem 7.1.6, this is sometimes equivalent to $f$ being continuous at $x$. Theorem 7.1.2 If $\lim {y \rightarrow x} f(y)=L$ and $\lim {y \rightarrow x} f(y)=L_{1}$, then $L=L_{1}$. Uniqueness also holds for one sided limits and for limits as $x \rightarrow \infty$ or $x \rightarrow-\infty$. Proof: Let $\varepsilon>0$ be given. There exists $\delta>0$ such that if $0<|y-x|<\delta$, then $$ |f(y)-L|<\varepsilon,\left|f(y)-L_{1}\right|<\varepsilon . $$ Therefore, for such $y,\left|L-L_{1}\right| \leq|L-f(y)|+\left|f(y)-L_{1}\right|<\varepsilon+\varepsilon=2 \varepsilon$. Since $\varepsilon>0$ was arbitrary, this shows $L=L_{1}$. The argument is exactly the same in the case of one sided limits or. You simply need to have some $y$ close enough to $x$ on one side and in the case of limits at $\pm \infty$, you use $y$ such that $|y|$ is sufficiently large.

Another concept is that of a function having either $\infty$ or $-\infty$ as a limit. In this case, the values of the function do not ever get close to their target because nothing can be close to $\pm \infty$. Roughly speaking, the limit of the function equals $\infty$ if the values of the function are ultimately larger than any given number. More precisely:

Definition 7.1.3 If $f(x) \in \mathbb{R}$, then $\lim {y \rightarrow x} f(x)=\infty$ if for every number $l$, there exists $\delta>0$ such that whenever $|y-x|<\delta$, then $f(x)>l . \lim {x \rightarrow \infty} f(x)=\infty$ if for all $k$, there exists $l$ such that $f(x)>k$ whenever $x>l$. One sided limits and limits as the variable approaches $-\infty$, are defined similarly.

It may seem there is a lot to memorize here. In fact, this is not so because all the definitions are intuitive when you understand them. Everything becomes much easier when you understand the definitions. This is usually the way it works in mathematics.
In the following theorem it is assumed the domains of the functions are such that the various limits make sense. Thus, if $\lim {y \rightarrow x}$ is used, it is to be understood the function is defined on $(x-\delta, x) \cup(x, x+\delta)$ for some $\delta>0$. However, to avoid having to state things repetitively this symbol will be written to symbolize $\lim {y \rightarrow x+}$ or $\lim {y \rightarrow x-}$ and in either of these cases, it is understood the function is defined on an appropriate set Suppose $f$ is real valued and $\lim {y \rightarrow x} f(y)=L .$ If $f(y) \leq a$ all $y$ near $x$ either to the right or to the left of $x$, then $L \leq a$ and if $f(y) \geq a$ then $L \geq a$.

Proof: The proof of $7.2$ is left for you. It is like a corresponding theorem for continuous functions. Next consider $7.3$. Let $\varepsilon>0$ be given. Then by the triangle inequality,
$$
\begin{aligned}
|f g(y)-L K| & \leq|f g(y)-f(y) K|+|f(y) K-L K| \
& \leq|f(y)||g(y)-K|+|K||f(y)-L|
\end{aligned}
$$
There exists $\delta_{1}$ such that if $0<|y-x|<\delta_{1}$, then $|f(y)-L|<1$, and so for such $y$, and the triangle inequality, $|f(y)|<1+|L|$. Therefore, for $0<|y-x|<\delta_{1}$,

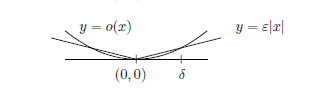
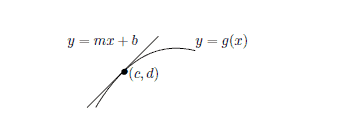
在本节中，函数将在 $\mathbb{R}$ 的某个子集上定义，其值在 $\mathbb{F}$ 中。需要 $\mathbb{R}$ 的限制是因为我们要考虑单边限制。

定义 7.1.1 令 $f$ 是一个定义在 $D(f)$ 上的函数，其中 $D(f) \supseteq$ $(xr, x) \cup(x, x+r)$ for some $r >0 .$ 请注意，$f$ 不一定在 $x$ 处定义。那么 $\lim {y \rightarrow x} f(y)=L$ 当且仅当以下条件成立。对于所有 $\varepsilon>0$ 存在 $\delta>0$ 使得如果 $$ 0<|y-x|<\delta, $$ 然后， $$ |L-f(y)|<\varepsilon \text {. } $$ 如果一切都和上面一样，除了 $y$ 需要大于 $x$ 并且 $f$ 只需要定义在 $(x, x+r)$ 上，那么符号是 $$ \lim {y \rightarrow x+} f(y)=L \text {. }
$$
如果 $f$ 只需要在 $(x-r, x)$ 上定义，并且 $y$ 需要小于 $x$，在与上述相同的条件下，我们写
$$
\lim {y \rightarrow x-} f(y)=L \text {。 } $$ 限制也被视为变量“接近”无穷大。当然，没有什么是“接近”无穷大的，因此这需要稍微不同的定义。 $$ \lim {x \rightarrow \infty} f(x)=L
$$
如果对于每个 $\varepsilon>0$ 存在 $l$ 使得每当 $x>l$，
$$
|f(x)-L|<\伐普西隆 $$ 第 7 章导数 123 $\lim {x \rightarrow-\infty} f(x)=L$ 左图中显示了一个函数的图形。注意 $x$ 处的函数值等于 $c$ 而 $\lim {y \rightarrow x+} f(y)=b$ 和 $\lim {y \rightarrow x-} f(y)=a美元。在第二张图中，$\lim {y \rightarrow x} f(y)=b$。请注意，在任何这些情况下，函数在点 $x$ 处的值都与函数的极限无关。 $x$ 处的函数值与 $x !$ 处的限制值无关，必须始终牢记这一点。您不会通过计算 $f(x) 来评估有趣的极限！$ 在上图中，$f(x)$ 总是错误的！ $f(x)$ 可能是正确的，但这只是一个巧合，正如下面定理 7.1.6 中所解释的，这有时等同于 $f$ 在 $x$ 处是连续的。定理 7.1.2 如果 $\lim {y \rightarrow x} f(y)=L$ 且 $\lim {y \rightarrow x} f(y)=L_{1}$，则 $L=L_{ 1}$。唯一性也适用于单边限制和 $x \rightarrow \infty$ 或 $x \rightarrow-\infty$ 的限制。证明：设$\varepsilon>0$。存在 $\delta>0$ 使得如果 $0<|y-x|<\delta$，那么 $$ |f(y)-L|<\varepsilon,\left|f(y)-L_{1}\right|<\varepsilon 。 $$ 因此，对于这样的 $y，\left|L-L_{1}\right| \leq|L-f(y)|+\left|f(y)-L_{1}\right|<\varepsilon+\varepsilon=2 \varepsilon$。由于 $\varepsilon>0$ 是任意的，这表明 $L=L_{1}$。在单边限制或的情况下，论点完全相同。您只需要在一侧有一些足够接近 $x$ 的 $y$，并且在 $\pm \infty$ 的限制的情况下，您使用 $y$ 使得 $|y|$ 足够大。

另一个概念是具有 $\infty$ 或 $-\infty$ 作为限制的函数。在这种情况下，函数的值永远不会接近它们的目标，因为没有任何东西可以接近 $\pm \infty$。粗略地说，如果函数的值最终大于任何给定的数字，则函数的极限等于 $\infty$。更确切地说：

定义 7.1.3 如果 $f(x) \in \mathbb{R}$，则 $\lim {y \rightarrow x} f(x)=\infty$ 如果对于每个数 $l$，存在 $\ delta>0$ 使得每当 $|yx|<\delta$, 然后 $f(x)>l 。 \lim {x \rightarrow \infty} f(x)=\infty$ 如果对于所有 $k$，存在 $l$ 使得当 $x>l$ 时 $f(x)>k$。单边限制和变量接近 $-\infty$ 时的限制的定义类似。

这里似乎有很多东西要记住。事实上，情况并非如此，因为当您理解所有定义时，它们都是直观的。当您了解定义时，一切都会变得容易得多。这通常是它在数学中的工作方式。
在以下定理中，假设函数的域使得各种限制都有意义。因此，如果使用 $\lim {y \rightarrow x}$，可以理解该函数是在 $(x-\delta, x) \cup(x, x+\delta)$ 上定义的一些增量> 0 $。然而，为了避免重复陈述，这个符号将被写成象征 $\lim {y \rightarrow x+}$ 或 $\lim {y \rightarrow x-}$ 并且在这两种情况下，可以理解该函数在适当的集合上定义假设 $f$ 是实值且 $\lim {y \rightarrow x} f(y)=L .$ 如果 $f(y) \leq a$ all $y$ 在 $x$ 附近$x$ 的左边，然后 $L \leq a$ 并且如果 $f(y) \geq a$ 然后 $L \geq a$。

证明：$7.2$ 的证明留给你。它就像连续函数的对应定理。接下来考虑 7.3 美元。设$\varepsilon>0$。然后由三角不等式，
$$
\开始{对齐}
|f g(y)-L K| & \leq|f g(y)-f(y) K|+|f(y) K-L K| \
& \leq|f(y)||g(y)-K|+|K||f(y)-L|
\end{对齐}
$$
存在 $\delta_{1}$ 使得如果 $0<|y-x|<\delta_{1}$，则 $|f(y)-L|