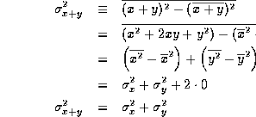物理代考| A Second Experiment — π0 Decay 量子力学代写
物理代写
$8.3$ A Second Experiment – $\pi^{0}$ Decay
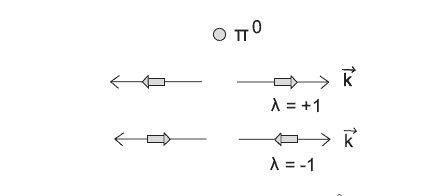
As a second, more complex, experiment, consider observations of the decay into two photons of the neutral, spin-zero, $\pi^{0}$ meson. We work in an abstract occupation number space where there are three states (see Fig. 8.3)
O ח $^{0}$
$\longleftrightarrow \longmapsto n \underset{\lambda=+1}{\stackrel{\square}{\longrightarrow}} \vec{k}$
$\longleftrightarrow \stackrel{\Leftrightarrow}{\Leftrightarrow} \underset{\lambda=-1}{\longleftrightarrow} \vec{k}$
Fig. $8.3$ The three states used in the discussion of the $\pi^{0}$-decay experiment.
(1) There is a single $\pi^{0}$ at rest in the state $\left|\pi^{0}\right\rangle$;
(2) There is one two-photon state with equal and opposite wave vectors $\vec{k}$ and unit positive helicities $\lambda=+1$, where the helicity is the component of the angular momentum along the direction of motion. With the use of the photon operators $b_{\vec{k} \lambda}^{\dagger}$ this state is
$$
|\vec{k},+1\rangle|-\vec{k},+1\rangle=b_{\vec{k},+1}^{\dagger} b_{-\vec{k},+1}^{\dagger}|0\rangle
$$
(3) There is a similar two-photon state with equal and opposite wave vectors $\vec{k}$ and unit negative helicities $\lambda=-1$
$$
|\vec{k},-1\rangle|-\vec{k},-1\rangle=b_{\vec{k},-1}^{\dagger} b_{-\vec{k},-1}^{\dagger}|0\rangle
$$
Since the pion at rest has no angular momentum, and angular momentum is conserved, there can be no net angular momentum along the direction of motion of the photons, and therefore it is only two-photon states with the same helicity that can be accessed during the decay. The state we are describing in the abstract occupation number space is a linear combination
$\qquad \Psi(t)\rangle=\int \frac{d \Omega_{k}}{2 \pi}\left{c_{+}(t)|\vec{k},+1\rangle|-\vec{k},+1\rangle+c_{-}(t)|\vec{k},-1\rangle|-\vec{k},-1\rangle\right}$ $\quad+c_{0}(t)\left|\pi^{0}\right\rangle$ $\quad$ Introduction to Quantum Mechanics
72 of these three states ${ }^{5}$
The Schrödinger equation then tracks all three coefficients in this state vector as a function of time.
- At the initial time $t=0$ we prepare a $\pi^{0}$ at rest so that
$$
c_{0}(0)=1 \quad ; c_{+}(0)=c_{-}(0)=0
$$ - There is a piece of the hamiltonian $H$ that converts the $\pi_{0}$ to two photons; we do not need to know just what this is, only that it is there. As the time progresses, the $\pi^{0}$ will disappear and the two photons will
appear. The decrease in $\left|c_{0}(t)\right|^{2}$ with time gives the decay rate, - After some time, the $\pi_{0}$ is gone, and the state is
$$
|\Psi(t)\rangle=\int \frac{d \Omega_{k}}{2 \pi}\left{c_{+}(t)|\vec{k},+1\rangle|-\vec{k},+1\rangle+c_{-}(t)|\vec{k},-1\rangle|-\vec{k},-1\rangle\right}
$$
With no further information, we expect these coefficients to be equal
Now suppose we do an experiment where we set up a detector to look at the photon with a given momentum $\hbar \vec{k}$ coming from the decay of a pion, and we measure the helicity of that photon. We do that experiment over obtained from Eq. (8.18). It is equally likely that we will measure $\lambda=+1$ as $\lambda=-1$. If we do measure $\lambda=+1$ in a pure pass measurement, for example, then the state vector becomes
$$
|\Psi(t)\rangle=c(t)|\vec{k},+1\rangle|-\vec{k},+1\rangle \quad ;|c(t)|^{2}=1
$$
We have reduced the basis, and the measurement is now reproducible. Let us do another experiment. We have a collaborator who sets up a second detector to measure the helicity of the second photon with opposite momentum $-\hbar \vec{k}$. If there is no coordination in our measurements, he or
物理代考
$8.3$ 第二次实验 – $\pi^{0}$ 衰减
作为第二个更复杂的实验,考虑观察到中性、自旋零、$\pi^{0}$ 介子的两个光子的衰变。我们在一个抽象的占用数空间中工作,其中存在三种状态(见图 8.3)
O ח $^{0}$
$\longleftrightarrow \longmapsto n \underset{\lambda=+1}{\stackrel{\square}{\longrightarrow}} \vec{k}$
$\longleftrightarrow \stackrel{\Leftrightarrow}{\Leftrightarrow} \underset{\lambda=-1}{\longleftrightarrow} \vec{k}$
图 $8.3$ $\pi^{0}$-decay 实验讨论中使用的三种状态。
(1) 在状态$\left|\pi^{0}\right\rangle$ 中存在一个静止的$\pi^{0}$;
(2) 存在一种双光子状态,波矢相等且相反,单位正螺旋度$\lambda=+1$,其中螺旋度是角动量沿运动方向的分量.使用光子算子 $b_{\vec{k} \lambda}^{\dagger}$ 这个状态是
$$
|\vec{k},+1\rangle|-\vec{k},+1\rangle=b_{\vec{k},+1}^{\dagger} b_{-\vec{k},+ 1}^{\匕首}|0\rangle
$$
(3) 有一个相似的双光子态,具有相等和相反的波向量 $\vec{k}$ 和单位负螺旋度 $\lambda=-1$
$$
|\vec{k},-1\rangle|-\vec{k},-1\rangle=b_{\vec{k},-1}^{\dagger} b_{-\vec{k},- 1}^{\匕首}|0\rangle
$$
由于静止的π介子没有角动量,而且角动量守恒,所以沿光子运动方向不可能有净角动量,因此只能得到具有相同螺旋度的双光子态。衰变。我们在抽象占用数空间中描述的状态是线性组合
$\qquad \Psi(t)\rangle=\int \frac{d \Omega_{k}}{2 \pi}\left{c_{+}(t)|\vec{k},+1\rangle |-\vec{k},+1\rangle+c_{-}(t)|\vec{k},-1\rangle|-\vec{k},-1\rangle\right}$ $\ quad+c_{0}(t)\left|\pi^{0}\right\rangle$ $\quad$ 量子力学导论
这三个州中的 72 个 ${ }^{5}$
然后,薛定谔方程跟踪该状态向量中的所有三个系数作为时间的函数。
- 在初始时间 $t=0$ 我们准备一个 $\pi^{0}$ 静止的,这样
$$
c_{0}(0)=1 \quad ; c_{+}(0)=c_{-}(0)=0
$$ - 有一块哈密顿 $H$ 将 $\pi_{0}$ 转换为两个光子;我们不需要知道这是什么,只需要知道它就在那里。随着时间的推移,$\pi^{0}$ 会消失,两个光子会
出现。 $\left|c_{0}(t)\right|^{2}$ 随时间的减少给出了衰减率, - 一段时间后,$\pi_{0}$ 消失了,状态变为
$$
|\Psi(t)\rangle=\int \frac{d \Omega_{k}}{2 \pi}\left{c_{+}(t)|\vec{k},+1\rangle|- \vec{k},+1\rangle+c_{-}(t)|\vec{k},-1\rangle|-\vec{k},-1\rangle\right}
$$
在没有进一步信息的情况下,我们希望这些系数相等
现在假设我们做一个实验,我们设置一个探测器来观察具有给定动量 $\hbar \vec{k}$ 的光子,该动量来自一个π介子的衰变,并且我们测量该光子的螺旋度。我们对从方程式获得的实验进行了实验。 (8.18)。我们同样可能将 $\lambda=+1$ 测量为 $\lambda=-1$。例如,如果我们确实在纯通过测量中测量 $\lambda=+1$,那么状态向量变为
$$
|\Psi(t)\rangle=c(t)|\vec{k},+1\rangle|-\vec{k},+1\rangle \quad ;|c(t)|^{2}= 1
$$
我们已经减少了基础,并且测量现在可以重现。让我们再做一个实验。我们有一个合作者,他设置了第二个探测器来测量具有相反动量 $-\hbar \vec{k}$ 的第二个光子的螺旋度。如果我们的测量没有协调,他或

物理代考| Classical Optics量子力学代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程