物理代考| Stern–Gerlach Experiment 量子力学代写
物理代写
8.1 Stern-Gerlach Experiment
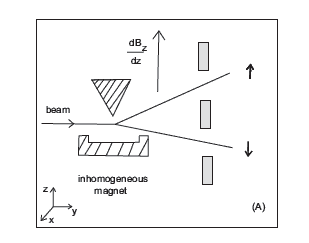
In this experiment a beam of neutral particles with internal angular momentum $\hbar \overrightarrow{\mathcal{S}}$, here assumed to be spin-1/2 with $\mathcal{S}_{z}=\pm 1 / 2$, and a magnetic moment $\vec{\mu}=2 \mu \overrightarrow{\mathcal{S}}$ in the direction of the spin, is passed through an inhomogeneous magnetic field (see Fig. 8.1).
Fig. $8.1$ Stern-Gerlach experiment on a spin-1/2 system with a magnetic moment $\vec{\mu}=$ $2 \mu \overrightarrow{\mathcal{S}}$, and $\mathcal{S}{\Sigma}=\pm 1 / 2$. The $z$-axis is in the plane and vertical. 67 68 Introduction to Quantum Mechanics The particles feel a force in the $z$-direction of $$ F{z}=\mu_{z} \frac{d B_{z}}{d z}
$$
Instead of seeing a continuous distribution of particles coming out of the detector in the $z$-direction, one observes only two beams, corresponding to $\mathcal{S}{z}=\pm 1 / 2$. This illustrates the discrete quantization of the angular momentum. One observes just the eigenvalues of $\mathcal{S}{z}$.
In quantum mechanics we understand what is happening by saying the initial internal state of each particle is a linear combination of the two spin states ${ }^{1}$
The probability that we will measure spin up is then $\left|c_{\uparrow}(t)\right|^{2}$, and the probability that we will measure spin down is $\left|c_{\downarrow}(t)\right|^{2}$, where
$$
\left|c_{\uparrow}(t)\right|^{2}+\left|c_{\downarrow}(t)\right|^{2}=1
$$
The internal Schrödinger equation tracks the behavior of both components as time progresses.
Suppose one now passes the top beam through a second detector identical to the first one as illustrated in Fig. 8.2.
Fig. $8.2$ Repeat of Stern-Gerlach experiment on upper beam using detector (A).
One will now observe that all of the particles coming out again have their spin up, and there are none coming out with their spin down. ${ }^{2}$ We conclude from this that measurements are reproducible, and if we measure that the particle has spin up, then another measurement immediately afterwards will again say that it has spin up.
${ }^{1}$ Here the states $|\uparrow\rangle$ and $|\downarrow\rangle$ are one-particle states in the abstract occupation number
space. 2We assume pure pass measurements here.
Quantum Measurements
69
But in quantum mechanics, we actually have something more profound. The act of the first measurement has changed the system. It is no longer in the state in Eq. (8.2). The act of measurement has reduced the basis. The act of measurement has placed it entirely in the new state
$$
\left|\psi_{\text {int }}(t)\right\rangle=c(t)|\uparrow\rangle \quad ;|c(t)|^{2}=1
$$
物理代考
8.1 Stern-Gerlach 实验
在这个实验中,一束具有内部角动量 $\hbar \overrightarrow{\mathcal{S}}$ 的中性粒子束,这里假设为自旋 1/2 且 $\mathcal{S}_{z}=\pm 1 / 2$ 和一个沿自旋方向的磁矩 $\vec{\mu}=2 \mu \overrightarrow{\mathcal{S}}$ 通过一个不均匀的磁场(见图 8.1)。
图 $8.1$ Stern-Gerlach 在自旋 1/2 系统上的实验,磁矩 $\vec{\mu}=$ $2 \mu \overrightarrow{\mathcal{S}}$, 和 $\mathcal{S} {\Sigma}=\pm 1 / 2$。 $z$ 轴在平面上并且是垂直的。 67 68 量子力学导论 粒子在 $z$ 方向上感觉到力 $$ F{z}=\mu_{z} \frac{d B_{z}}{d z}
$$
与其看到从探测器出来的粒子在 $z$ 方向上的连续分布,人们只观察到两束光束,对应于 $\mathcal{S}{z}=\pm 1 / 2$。这说明了角动量的离散量化。人们只观察 $\mathcal{S}{z}$ 的特征值。
在量子力学中,我们通过说每个粒子的初始内部状态是两个自旋状态 ${ }^{1}$ 的线性组合来理解正在发生的事情
那么我们测量自旋向上的概率是$\left|c_{\uparrow}(t)\right|^{2}$,我们测量自旋向下的概率是$\left|c_{\downarrow} (t)\right|^{2}$, 其中
$$
\left|c_{\uparrow}(t)\right|^{2}+\left|c_{\downarrow}(t)\right|^{2}=1
$$
随着时间的推移,内部薛定谔方程跟踪两个组件的行为。
假设现在让顶部光束通过与第一个检测器相同的第二个检测器,如图 8.2 所示。
图 $8.2$ 使用探测器 (A) 在上光束上重复 Stern-Gerlach 实验。
现在可以观察到,所有再次出来的粒子都自旋向上,而没有一个粒子随着自旋向下而出现。 ${ }^{2}$ 我们由此得出结论,测量是可重复的,如果我们测量粒子已经自旋,那么紧接着的另一个测量将再次说它已经自旋。
${ }^{1}$ 这里的状态 $|\uparrow\rangle$ 和 $|\downarrow\rangle$ 是抽象占用数中的单粒子状态
空间。 2我们在这里假设纯通过测量。
量子测量
69
但在量子力学中,我们实际上有更深奥的东西。第一次测量的行为改变了系统。它不再处于方程式中的状态。 (8.2)。测量行为减少了基础。测量的行为使它完全处于新的状态
$$
\left|\psi_{\text {int }}(t)\right\rangle=c(t)|\uparrow\rangle \quad ;|c(t)|^{2}=1
$$

物理代考| Classical Optics量子力学代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程