物理代写| Introduction 相对论代考
物理代写
3.1 Introduction
We have seen that gravitation is a manifestation of the curvature of spacetime. The mathematical structure which describes the physical situation had already been worked out by Gauss and Riemann several decades before Einstein conceived of GR. So the mathematical tools already existed for Einstein to use in his theory. The mathematical structure is the differentiable manifold-the spacetime of GR is a 4-dimensional differentiable manifold with the addition of a metric. Differentiable manifolds on which a metric is defined are called Riemannian manifolds. The metric is a second rank tensor. Thus one needs to understand and develop the algebra and calculus of tensors in order to proceed with GR. We will do this here step by step instead of launching directly into tensors on manifolds. We will first consider flat spaces like the spacetime of special relativity in which there is no gravity and in particular $n$ dimensional Euclidean spaces with which the student is usually familiar. In SR we have already encountered the quantity $\eta_{\mu v}$ which is in fact an example of a second rank tensor but only under Lorentz transformations. However, in GR we operate with general coordinate transformations so that the tensors and in particular the metric tensor transforms under general coordinate transformations-the scope is wider. Lot of the tools such as tensor algebra and also the analysis to a large extent can be developed in flat spaces and for making a smooth transition to general curved spaces we will do so in general curvilinear coordinate systems. The advantage here is that in flat space we can always choose a Cartesian coordinate system globally pervading the entire space in which the metric coefficients are constants. We can therefore use this as an “anchor” to obtain our results. This is not so for a curved space where one must necessarily use curvilinear coordinate systems-in fact more than one of them to entirely cover the manifold. These statements will become clear later and will be validated in the text as we go along. So by the approach adopted here, we are taking one step at a time.
There is another advantage to starting with a flat space. The quantities such as vectors and tensors are elements of certain vector spaces which are associated with
(C) The Author(s), under exclusive license to Springer Nature Switzerland AG 2022
37
S. Dhurandhar and S. Mitra, General Relativity and Gravitational Waves,
UNITEXT for Physics, https://doi.org/10.1007/978-3-030-92335-8_3
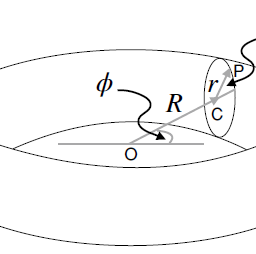
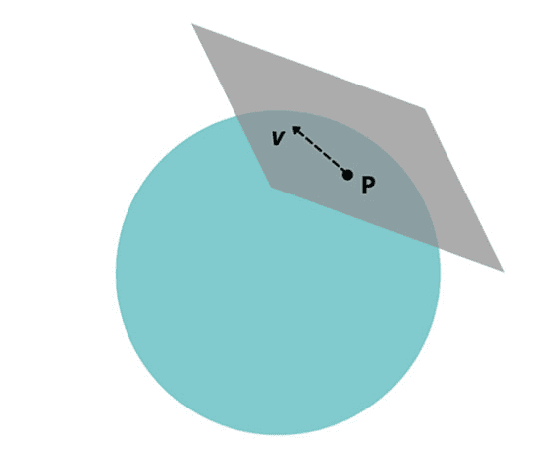
Fig. 3.1 The shaded plane is a tangent plane to the sphere at the point $\mathrm{P}$ on the sphere. The tangent plane consists of vectors such as $\mathbf{v}$. Note that the vector $\mathbf{v}$ is distinct from any point on the sphere. Credits: Ankit Bhandari
the differentiable manifold but the vectors or tensors are not elements of the manifold. The tangent space at a point of a manifold plays an important role-the (contravariant) vectors belong to this vector space. For example, consider the usual sphere which is a 2 dimensional manifold. At any point $\mathrm{P}$ on the sphere we can draw a tangent plane which consists of vectors tangent to the sphere’s surface. These vectors are not in the sphere and the tangent plane is distinct from the sphere [see Fig. 3.1]. More importantly we cannot associate vectors on the plane in a unique way with the points on the sphere. On the other hand, the situation is different for the plane. Although the tangent space at any point of the plane is distinct from the plane (the manifold) itself, we can identify the two-to each vector in the tangent plane we can uniquely identify a point in the plane. We have the so called “position vectors”. We can talk of position vectors without ambiguity and use them to our advantage. Tensors are elements of vector spaces built up essentially from the tangent space and its dual (vector space of linear mappings from the tangent space to the real numbers-this is also a vector space with the same dimension as the tangent space and is called the cotangent space). The tangent space has the same dimension as the manifold. A differentiable manifold is locally flat. For example a small region of the sphere looks like a plane. This is the reason why ancient people thought that the earth was flat-a region the size of few kilometres looks flat although the earth is approximately a sphere. For this purpose the size of the region must be small compared with the radius of the earth. Generally, at each point of the manifold, we can construct a tangent space because the manifold is locally flat. This is the key reason why we will
3.1 Introduction
39
be able to port the results of tensor algebra obtained for a flat space on to a curved manifold. At this point there is no loss of generality to our approach.
In this book we will not enter into the formal discussion of modern mathematics mentioned in the previous paragraph, but we will take a toned down and intuitive approach which will essentially give sufficient understanding of the subject, and further deduce and appreciate the results obtained in this book.
物理代考
.1 简介
我们已经看到,万有引力是时空弯曲的表现。描述物理情况的数学结构早在爱因斯坦构思 GR 之前几十年就已经由高斯和黎曼制定。因此,爱因斯坦在他的理论中使用的数学工具已经存在。数学结构是可微流形——GR的时空是一个4维可微流形加上一个度量。定义度量的可微流形称为黎曼流形。该度量是二阶张量。因此,为了继续研究 GR,需要理解和发展张量的代数和微积分。我们将在此处逐步执行此操作,而不是直接启动流形上的张量。我们将首先考虑平面空间,如狭义相对论中没有引力的时空,尤其是学生通常熟悉的 $n$ 维欧几里得空间。在 SR 中,我们已经遇到了量 $\eta_{\mu v}$,它实际上是二阶张量的一个例子,但仅在洛伦兹变换下。然而,在 GR 中,我们使用一般坐标变换进行操作,因此张量,特别是在一般坐标变换下的度量张量变换 – 范围更广。许多工具(例如张量代数)以及很大程度上的分析可以在平面空间中开发,并且为了平滑过渡到一般弯曲空间,我们将在一般曲线坐标系中进行。这里的优点是,在平面空间中,我们总是可以选择一个笛卡尔坐标系全局遍布整个空间,其中度量系数是常数。因此,我们可以将其用作“锚”来获得我们的结果。对于一个必须使用曲线坐标系的弯曲空间,情况并非如此——事实上,要完全覆盖流形的不止一个。这些陈述将在稍后变得清晰,并将在我们继续进行时在文本中得到验证。因此,通过这里采用的方法,我们一次迈出一步。
从平坦的空间开始还有另一个好处。向量和张量等量是某些向量空间的元素,它们与
(C) 作者,获得 Springer Nature Switzerland AG 2022 的独家许可
37
S. Dhurandhar 和 S. Mitra,广义相对论和引力波,
UNITEXT 物理,https://doi.org/10.1007/978-3-030-92335-8_3
图 3.1 阴影平面是球体上点 $\mathrm{P}$ 处的切平面。切平面由诸如$\mathbf{v}$之类的向量组成。请注意,向量 $\mathbf{v}$ 不同于球体上的任何点。致谢:Ankit Bhandari
可微流形,但向量或张量不是流形的元素。流形一点的切线空间起着重要的作用——(逆变)向量属于这个向量空间。例如,考虑通常的球体,它是一个二维流形。在球体上的任何点$\mathrm{P}$,我们可以绘制一个切平面,它由与球体表面相切的向量组成。这些向量不在球体中,切平面与球体不同[见图 3.1]。更重要的是,我们不能以独特的方式将平面上的向量与球体上的点相关联。另一方面,飞机的情况有所不同。尽管平面任意点的切线空间与平面(流形)本身不同,但我们可以识别切平面中的每一个向量,我们可以唯一地识别平面中的一个点。我们有所谓的“位置向量”。我们可以毫不含糊地谈论位置向量,并将它们用于我们的优势。张量是向量空间的元素,本质上是从切空间及其对偶(从切空间到实数的线性映射的向量空间-这也是与切空间具有相同维度的向量空间,称为余切)空间)。切线空间与流形具有相同的维度。可微流形是局部平坦的。例如,球体的一个小区域看起来像一个平面。这就是为什么古人认为地球是平的——一个几公里大小的区域看起来是平的,虽然地球近似于一个球体。为此,该区域的大小必须小于地球的半径。一般来说,在流形的每一点,我们可以构造一个切空间,因为流形是局部平坦的。这是我们将
3.1 简介
39
能够将针对平坦空间获得的张量代数的结果移植到弯曲的流形上。在这一点上,我们的方法没有失去一般性。
在本书中,我们不会进入前一段中提到的现代数学的正式讨论,但我们将采用一种温和而直观的方法

物理代考Gravity and Curvature of Space-Time 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程