物理代写| Kerr Spacetime and the Rotating Black Hole 相对论代考
物理代写
6.6.1 The Metric and the Horizon
From the astrophysical point of view, a purely non-rotating black hole would be unlikely. Generically, a black-hole would possess spin or non-zero angular momentum. The black holes found in the past few years by the gravitational wave observatories LIGO and Virgo are all in general, spinning having non-negligible angular momentum. Only if the angular momentum is found to be small, then the Schwarzschild solution would approximately be applicable. In this section we briefly describe the rotating black hole which is embodied in the Kerr solution (1963) which describes the spacetime outside a spinning mass. This is perhaps the most important exact solution of Einstein’s equation apart from the Schwarzschild.
We write down the metric for a mass $M$ with angular momentum $J$ in BoyerLindquist coordinates:
$$
\begin{aligned}
d s^{2}=&\left(1-\frac{2 m r}{\Sigma}\right) c^{2} d t^{2}-\frac{\Sigma}{\Delta} d r^{2}-\Sigma d \theta^{2}-\left(r^{2}+a^{2}+\frac{2 m a^{2} r \sin ^{2} \theta}{\Sigma}\right) \sin ^{2} \theta d \phi^{2} \
&+\frac{4 m r a \sin ^{2} \theta}{\Sigma} c d t d \phi,
\end{aligned}
$$
116
6 Schwarzschild Solution and Black Holes
where $a=J / c M$ is the angular momentum per unit mass of the black hole and $m=G M / c^{2}$. Both $a$ and $m$ have dimensions of length. The quantities $\Delta$ and $\Sigma$ are defined by,
$$
\Delta=r^{2}-2 m r+a^{2}, \quad \Sigma=r^{2}+a^{2} \cos ^{2} \theta
$$
This is an axially symmetric solution. It is not spherically symmmetric like the Schwarzschild solution. If we put $a=0$ in the Kerr metric described by Eqs. (6.6.1) and (6.6.2), then the metric reduces to the Schwarzschild metric.
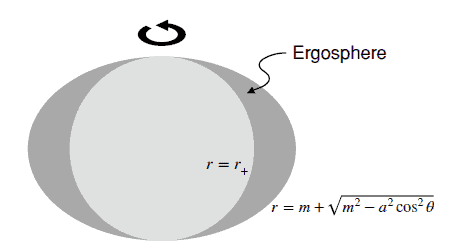
The horizon is given by the root of the equation $\Delta=0$. Since this is a quadratic, it has two roots $r_{\pm}$. The larger root $r_{+}=m+\sqrt{m^{2}-a^{2}}$ defines the horizon. The other root $r=r_{-}$also defines a horizon but since $r_{-}2 \mathrm{~m}$. These are called static observers. Now we ask the same question for the Kerr solution. An observer can remain at a fixed $(r, \theta, \phi)$ only when $g_{00}>0$. Note that the subscript 0 represents $x^{0}=c t$. Thus the limit for such observers is obtained when $g_{00}=0$ or when:
where the dot represents derivative with respect to the proper time $\tau$ (note we have absorbed the factor of $c$ so that we have the right dimensions for the constant) and
$6.6$ Kerr Spacetime and the Rotating Black Hole
117
also we have not explicitly written the metric. By taking limits as $r \longrightarrow \infty$, we find $g_{0 \phi} \longrightarrow 0$ while $g_{\phi \phi} \longrightarrow-r^{2} \sin ^{2} \theta$ and hence $g_{0 \phi} c \dot{t}+g_{\phi \phi} \dot{\phi} \longrightarrow-r^{2} \sin ^{2} \theta \dot{\phi} \equiv$ $-L$, where $L$ is the angular momentum per unit mass of the test particle at infinity. Thus the constant is $-L$ in Eq. (6.6.4). A particle starting from rest from infinity has $L=0$ (why?) and thus:
$$
\frac{d \phi}{d t}=\frac{\dot{\phi}}{\dot{t}}=-\frac{c g_{0 \phi}}{g_{\phi \phi}}=\omega(r, \theta)>0
$$
Therefore, such a particle as it falls into the black hole must co-rotate with the black hole. In fact if an observer has angular velocity $d \phi / d t=\omega(r, \theta)$ as given in Eq. $(6.6 .5)$, then such observers are called zero angular momentum observers or ZAMOs. They are also called locally non-rotating observers or LNROs. Such observers play an important role from the physical point of view. See Misner et al. (1973). All these effects go by the name of frame dragging.
Lastly, as Penrose argued, that the ergosphere can be used for energy extraction from the black hole. Consider the tangent vector $\xi$ to the coordinate $x^{0}=c t$ in this region. It is spacelike because $\xi \cdot \xi=g_{00}<0$. There exist time-like vectors whose scalar product with $\xi$ is negative (see Exercise 1). Thus, one can conceive of a momentum vector $\mathbf{p}$ (future time-like) whose scalar product with $\xi$ is negative, $\mathbf{p} \cdot \xi<0$. But this is just the energy at infinity $\mathcal{E}$ (Misner et al. (1973)). Therefore, one can have particles inside the ergosphere with momentum $\mathbf{p}$ such that $\mathbf{p} \cdot \xi=\mathcal{E}<0$. We can then arrange for a particle with energy $\mathcal{E}$ to come in from infinity and split into two particles inside the ergosphere with one of them having $\mathcal{E}{2}<0$. Because energy is conserved, we have $\mathcal{E}=\mathcal{E}{1}+\mathcal{E}{2}$, and so we have $\mathcal{E}{1}>\mathcal{E}$. This particle escapes to infinity with larger energy $\mathcal{E}{1}$ than the incoming particle which had energy $\mathcal{E}$. Thus we see that we can extract energy from a rotating black hole. This energy comes at the expense of the black hole losing rotational energy, because the particle with energy $\mathcal{E}{2}<0$ falls into the hole reducing its energy.
物理代考
6.6.1 度量和视野
从天体物理学的角度来看,纯粹的非旋转黑洞是不可能的。一般来说,黑洞会拥有自旋或非零角动量。引力波天文台LIGO和Virgo这几年发现的黑洞都是一般的,自转具有不可忽略的角动量。只有当发现角动量很小时,Schwarzschild 解才近似适用。在本节中,我们将简要描述旋转黑洞,它体现在克尔解(1963 年)中,描述了旋转质量之外的时空。这可能是爱因斯坦方程除了史瓦西方程之外最重要的精确解。
我们在 BoyerLindquist 坐标中写下具有角动量 $J$ 的质量 $M$ 的度量:
$$
\开始{对齐}
ds^{2}=&\left(1-\frac{2 mr}{\Sigma}\right) c^{2} dt^{2}-\frac{\Sigma}{\Delta} dr^{2 }-\Sigma d \theta^{2}-\left(r^{2}+a^{2}+\frac{2 ma^{2} r \sin ^{2} \theta}{\Sigma} \right) \sin ^{2} \theta d \phi^{2} \
&+\frac{4 m r a \sin ^{2} \theta}{\Sigma} c d t d \phi,
\end{对齐}
$$
116
6 史瓦西解和黑洞
其中$a=J / c M$是黑洞每单位质量的角动量,$m=G M / c^{2}$。 $a$ 和 $m$ 都有长度维度。数量 $\Delta$ 和 $\Sigma$ 由下式定义,
$$
\Delta=r^{2}-2 m r+a^{2}, \quad \Sigma=r^{2}+a^{2} \cos ^{2} \theta
$$
这是一个轴对称的解决方案。它不像 Schwarzschild 解那样是球对称的。如果我们将 $a=0$ 放入方程式描述的 Kerr 度量中。 (6.6.1) 和 (6.6.2),然后度量减少到 Schwarzschild 度量。
地平线由方程 $\Delta=0$ 的根给出。由于这是一个二次方程,它有两个根 $r_{\pm}$。较大的根 $r_{+}=m+\sqrt{m^{2}-a^{2}}$ 定义了地平线。另一个根 $r=r_{-}$ 也定义了一个地平线,但由于 $r_{-}2 \mathrm{~m }$。这些被称为静态观察者。现在我们对 Kerr 解决方案提出同样的问题。只有当 $g_{00}>0$ 时,观察者才能保持在固定的 $(r, \theta, \phi)$。注意下标0代表$x^{0}=c t$。因此,当 $g_{00}=0$ 或当:
其中点表示关于适当时间 $\tau$ 的导数(注意我们已经吸收了 $c$ 的因子,因此我们有常数的正确维度)和
$6.6$ 克尔时空和旋转黑洞
117
我们也没有明确写出指标。取极限为 $r \longrightarrow \infty$,我们发现 $g_{0 \phi} \longrightarrow 0$ 而 $g_{\phi \phi} \longrightarrow-r^{2} \sin ^{2} \theta $ 因此 $g_{0 \phi} c \dot{t}+g_{\phi \phi} \dot{\phi} \longrightarrow-r^{2} \sin ^{2} \theta \dot{\ phi} \equiv$ $-L$,其中 $L$ 是测试粒子在无穷远处的每单位质量的角动量。因此,方程中的常数是 $-L$。 (6.6.4)。从无穷大的静止开始的粒子有 $L=0$(为什么?),因此:
$$
\frac{d \phi}{dt}=\frac{\dot{\phi}}{\dot{t}}=-\frac{c g_{0 \phi}}{g_{\phi \phi}} =\omega(r, \theta)>0
$$
因此,落入黑洞的粒子必然与黑洞共同旋转。事实上,如果观察者的角速度 $d \phi / d t=\omega(r, \theta)$ 如公式 1 所示。 $(6.6 .5)$,那么这样的观察者被称为零角动量观察者或 ZAMO。它们也被称为局部非旋转观察者或 LNRO。从物理的角度来看,这些观察者起着重要的作用。见米斯纳等人。 (1973 年)。所有这些效果都称为帧拖动。
最后,正如彭罗斯所说,能层可用于从黑洞中提取能量。考虑该区域中坐标 $x^{0}=c t$ 的切向量 $\xi$。它是类空间的,因为 $\xi \cdot \xi=g_{00}<0$。存在与 $\xi$ 的标量积为负的类时向量(参见练习 1)。因此,可以设想一个动量向量 $\mathbf{p}$(类未来),其与 $\xi$ 的标量积为负,$\mathbf{p} \cdot \xi<0$。但这只是无穷大的能量 $\mathcal{E}$ (Misner et al. (1973))。因此,在能层内可以有动量为 $\mathbf{p}$ 的粒子,使得 $\mathbf{p} \cdot \xi=\mathcal{E}<0$。然后我们可以安排一个能量为 $\mathcal{E}$ 的粒子从无穷大进入并在能层内分裂成两个粒子,其中一个粒子的 $\mathcal{E}_{2}<0$。因为能量是守恒的,我们

物理代考Gravity and Curvature of Space-Time 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程