物理代写| Transition to Curved Spaces 相对论代考
物理代写
3.8 Transition to Curved Spaces
We can readily generalise the foregoing discussion to tensors on curved spaces o Riemannian manifolds. A Riemannian space, roughly speaking, can be thought o as a $n$ dimensional generalisation of a two dimensional surface on which a metric has been defined. Any Riemannian space can be embedded in a sufficiently higl dimensional Euclidean space-the maximum dimension required is $n(n+1) .$ The same result also holds for a pseudo-Riemannian space of given signature which can be embedded in a flat space with appropriate signature (Eisenhart (1926)). For example, a 3 -sphere can be embedded in the 4-dimensional Euclidean space-one does not need 6 dimensions because it happens to be a highly symmetric space. Consider a 4 dimensional Euclidean space with Cartesian coordinates $x^{i}, i=1,2,3,4$, then the equation $\left(x^{1}\right)^{2}+\left(x^{2}\right)^{2}+\left(x^{3}\right)^{2}+\left(x^{4}\right)^{2}=1$ describes a 3 dimensional unit sphere equation $\left(x^{1}\right)^{2}+\left(x^{2}\right)^{2}+\left(x^{3}\right)^{2}+\left(x^{4}\right)^{2}=1$ describes a 3 dimensional unit sphere embedded in 4 dimensions. Another example is the 4 dimensional Schwarzschild If one thinks of a curved space as a subspace of a higher dimensional flat space, then
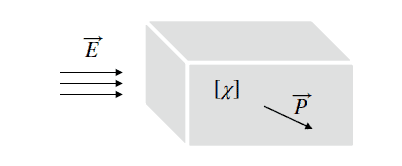
${ }^{2}$ For the advanced reader: Contravariant vectors (tangent vectors) and covariant vectors (1-forms) belong to different vector spaces, namely, the tangent space and the cotangent space respectively. However, the metric tensor defines an isomorphism between them by $V_{i}=g_{i j} V^{j}$ and its inverse $V^{i}=g^{i j} V_{j}$. This has been demonstrated pictorially in the example.
$3.8$ Transition to Curved Spaces
55
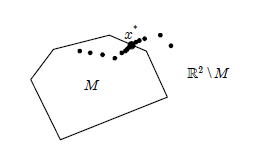
it inherits the metric – the induced metric-from that flat space. See Exercise $3.10$ for a 2 dimensional space (surface) embedded in 3 dimensional Euclidean space. Since we did not put any restriction on dimension of the spaces, all the foregoing discussion on vectors and tensors is valid for $n$ dimensional Riemannian manifolds.
However, embedding the curved space in a higher dimensional Euclidean space is not necessary-we can have a Riemannian space in its own right. We only need to prescribe a set of $n$ coordinates $x^{i}$ or a coordinate system in general on a subset of the space with sufficiently smoothness properties. This is called a chart. We generally require several charts to cover the space. In fact a curved space cannot be covered by a single chart. Now suppose we have another chart $x^{\prime j}$, then on the intersection of the two charts, we will have $x^{i i}$ s as functions of $x^{j}$ and vice-versa. In the intersection region of the two charts, the vectors and tensors follow exactly the same transformation laws as discussed earlier. Our analysis therefore is local and restricted to a chart or to an intersection region of charts. In this introductory book, we will restrict ourselves to local analysis. What about the metric? The metric must be prescribed. Since we do not have any Euclidean space in the background, the metric has to be given. It may be positive definite or indefinite as may be required from physical considerations. In relativity, both special and general, we have a 4 dimensional manifold on which the metric is indefinite.
Given these considerations, the foregoing discussion on vectors and tensors applies equally well to general $n$ dimensional Riemannian spaces.
物理代考
3.8 向弯曲空间的过渡
我们可以很容易地将上述讨论推广到弯曲空间或黎曼流形上的张量。粗略地说,黎曼空间可以被认为是定义度量的二维表面的$n$维泛化。任何黎曼空间都可以嵌入到足够高维的欧几里得空间中——所需的最大维数是$n(n+1)。同样的结果也适用于可以嵌入平面空间的给定签名的伪黎曼空间带有适当的签名(Eisenhart (1926))。例如,一个 3 球体可以嵌入到 4 维欧几里得空间中——一个不需要 6 维,因为它恰好是一个高度对称的空间。考虑一个笛卡尔坐标 $x^{i}, i=1,2,3,4$ 的 4 维欧几里得空间,那么方程 $\left(x^{1}\right)^{2}+\left( x^{2}\right)^{2}+\left(x^{3}\right)^{2}+\left(x^{4}\right)^{2}=1$ 描述了一个 3维单位球面方程 $\left(x^{1}\right)^{2}+\left(x^{2}\right)^{2}+\left(x^{3}\right)^{ 2}+\left(x^{4}\right)^{2}=1$ 描述了嵌入在 4 维中的 3 维单位球体。另一个例子是 4 维 Schwarzschild 如果将弯曲空间视为更高维平面空间的子空间,那么
${ }^{2}$ 对于高级读者:逆变向量(正切向量)和协变向量(1-形式)属于不同的向量空间,分别是正切空间和余切空间。然而,度量张量通过 $V_{i}=g_{i j} V^{j}$ 及其逆 $V^{i}=g^{i j} V_{j}$ 定义了它们之间的同构。这已在示例中以图形方式演示。
$3.8$ 过渡到弯曲空间
55
它从该平坦空间继承度量——诱导度量。有关嵌入在 3 维欧几里得空间中的 2 维空间(曲面),请参见练习 $3.10$。由于我们没有对空间的维数施加任何限制,所以前面关于向量和张量的所有讨论对于 $n$ 维黎曼流形都是有效的。
然而,将弯曲空间嵌入到更高维的欧几里得空间中并不是必须的——我们可以拥有自己的黎曼空间。我们只需要在具有足够平滑属性的空间子集上规定一组 $n$ 坐标 $x^{i}$ 或一般坐标系。这称为图表。我们通常需要几个图表来覆盖空间。事实上,一个弯曲的空间不能被一张图表覆盖。现在假设我们有另一个图表 $x^{\prime j}$,那么在两个图表的交点上,我们将有 $x^{ii}$ s 作为 $x^{j}$ 的函数,反之亦然.在两个图表的交集区域,向量和张量遵循与前面讨论的完全相同的变换定律。因此,我们的分析是局部的,并且仅限于图表或图表的交叉区域。在这本介绍性的书中,我们将仅限于局部分析。指标呢?必须规定度量标准。由于我们在背景中没有任何欧几里得空间,因此必须给出度量。根据物理考虑,它可以是肯定的或不确定的。在狭义和广义相对论中,我们有一个 4 维流形,其度量是不确定的。
鉴于这些考虑,前面关于向量和张量的讨论同样适用于一般的 $n$ 维黎曼空间。

物理代考Gravity and Curvature of Space-Time 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程