物理代写| The Energy-Momentum Stress Tensor 相对论代考
物理代写
5.2 The Energy-Momentum Stress Tensor
The distribution of matter in Einstein’s theory is described by the energy-momentum tensor $T^{i j}$. It is defined to be symmetric. The tensor in its simplest form describes a dust distribution which is characterised by just one function $\rho$, the density or the equivalently the energy density. Or it can describe what is called a perfect fluida fluid which obeys Pascal’s law in its rest frame—pressure is isotropic. We will describe the various cases and provide their expressions below. It can also describe even more complex systems. Below we mention the physical meaning of each of its components, with the indices $j, k$ taking values 1, 2, 3 only:
- $T^{00}$ is the energy density $\rho c^{2}$.
- $c T^{0 k}$ is the energy flux across the surface $x^{k}=$ const.
- $T^{k k}$ is the pressure on the surface $x^{k}=$ const.
90
5 Einstein’s Equations - In general $T^{j k}$ is the flux of the $j$ th component of momentum across the surface $x^{k}=$ const.. It represents spatial stresses.
- $c^{-1} T^{k 0}$ is the $k$ th component of the momentum-density.
In the above description, the indices $j, k$ take values $1,2,3$.
The above prescription shows that not only mass, but energy, momentum, pressure, elastic stresses all determine the curvature of spacetime or the gravitational field. They are all sources of gravitation. We may contrast this situation with Newton’s theory in which it was only the mass density which produced the gravitational field. A simple example will illustrate this. Consider a sphere of uniform density $\rho_{0}$ and consider the following two situations: (i) the sphere does not rotate, (ii) the sphere rotates with some constant angular velocity. In Newton’s theory there will be no difference in the gravitational field in the two situations, because the distribution of $\rho$ in the two cases will be identical. But in Einstein’s theory, it is the energy momentum tensor that is tere will also be a non-zero momentum flux as distinct from the first, and also other differences and so the energy momentum tensors will differ in the two cases, giving rise to different gravitational fields. For the rotating sphere, one effect is the dragging of inertial frames-we will discuss this later in the context of rotating black holes.
We now give some important examples of energy momentum tensors. The simplest case is that of dust or a dust cloud. Here there is no pressure and no elastic stresses. It is given by the expression:
$$
T^{i k}=\rho c^{2} u^{i} u^{k} .
$$
Here $\rho$ is the density of matter and $u^{i}$ is the 4-velocity of the matter. Such a tensor is used in cosmology to obtain the Friedmann models of the universe. The Earth too can be considered to be dust. We may expect the pressure to be maximum near the centre of the Earth. It is of the order of $10^{12}-10^{13}$ dynes per square $\mathrm{cm}$, while the average mass density is $\sim 5.5 \mathrm{gm} / \mathrm{cc}$. We must compare $p / c^{2}$ with $\rho$ and this turns out to be $p / \rho c^{2} \sim 10^{-9}$. Thus the pressure can be ignored to compute the gravity due to Earth. The same is true for other components of $T^{i k}$, except $T^{00}$ which is the only surviving component. Thus this is the only component, namely the mass density, which is responsible for the gravitational field of the Earth just as in Newton’s theory. for weak fields and slow motion. It is therefore advisable to use the simpler theory of Newton to compute the gravitational field of the Earth for the usual day to day situations.
We now consider the case of the perfect fluid. Consider a fluid element and go to its rest frame. In this frame assume Pascal’s law that the pressure is the same in all directions. Choose also locally flat coordinates so that the metric tensor upto the first order is $\eta_{i k}$, the metric of SR. The energy-momentum tensor in this frame is diagonal and is given by:
物理代考
5.2 能量-动量应力张量
爱因斯坦理论中的物质分布是用能量-动量张量$T^{i j}$来描述的。它被定义为对称的。张量以其最简单的形式描述了一种尘埃分布,其特征在于只有一个函数 $\rho$,即密度或等效的能量密度。或者它可以描述在静止框架中遵循帕斯卡定律的所谓完美流体——压力是各向同性的。我们将描述各种情况并在下面提供它们的表达方式。它还可以描述更复杂的系统。下面我们提到它的每个组件的物理含义,索引 $j、k$ 仅取值 1、2、3:
- $T^{00}$ 是能量密度 $\rho c^{2}$。
- $c T^{0 k}$ 是表面的能量通量 $x^{k}=$ const。
- $T^{k k}$ 是曲面上的压力 $x^{k}=$ const。
90
5 爱因斯坦方程 - 一般来说,$T^{j k}$ 是第 $j$ 个动量分量在表面上的通量 $x^{k}=$ const.. 它代表空间应力。
- $c^{-1} T^{k 0}$ 是动量密度的第 $k$ 个分量。
在上面的描述中,索引 $j, k$ 取值 $1,2,3$。
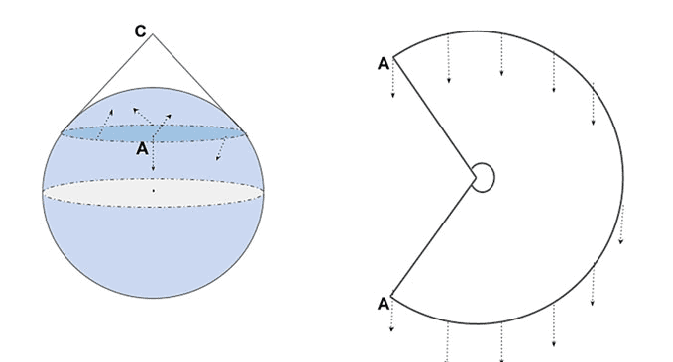
上述规定表明,不仅质量,而且能量、动量、压力、弹性应力都决定时空曲率或引力场。它们都是万有引力的来源。我们可以将这种情况与牛顿的理论进行对比,在牛顿理论中,只有质量密度产生了引力场。一个简单的例子将说明这一点。考虑一个密度均匀的球体 $\rho_{0}$ 并考虑以下两种情况:(i)球体不旋转,(ii)球体以恒定的角速度旋转。在牛顿的理论中,两种情况下的引力场没有区别,因为两种情况下$\rho$的分布是相同的。但是在爱因斯坦的理论中,能量动量张量也是一个与第一个不同的非零动量通量,还有其他差异,因此能量动量张量在两种情况下会有所不同,从而产生不同的引力场。对于旋转球体,一个影响是惯性框架的拖动——我们稍后将在旋转黑洞的背景下讨论这个问题。
我们现在给出一些能量动量张量的重要例子。最简单的情况是尘埃或尘云。这里没有压力,也没有弹性应力。它由表达式给出:
$$
T^{i k}=\rho c^{2} u^{i} u^{k} 。
$$
这里 $\rho$ 是物质的密度,$u^{i}$ 是物质的 4 速度。这样的张量在宇宙学中用于获得宇宙的弗里德曼模型。地球也可以被认为是尘埃。我们可以预期压力在地球中心附近最大。它的数量级为每平方 $\mathrm{cm}$ 10^{12}-10^{13}$ 达因,而平均质量密度为 $\sim 5.5 \mathrm{gm} / \mathrm{cc}美元。我们必须将 $p / c^{2}$ 与 $\rho$ 进行比较,结果是 $p / \rho c^{2} \sim 10^{-9}$。因此,在计算地球引力时可以忽略压力。 $T^{ik}$ 的其他组件也是如此,除了 $T^{00}$ 是唯一幸存的组件。因此,这是唯一的组成部分,即质量密度,与牛顿理论一样,它负责地球的引力场。适用于弱场和慢动作。因此,建议使用更简单的牛顿理论来计算日常情况下地球的引力场。
我们现在考虑完美流体的情况。考虑一个流体元素并转到它的静止框架。在这个框架中假设压力在所有方向上都是相同的帕斯卡定律。还要选择局部平面坐标,以便直到一阶的度量张量是 $\eta_{ik}$,即 SR 的度量。该框架中的能量-动量张量是对角线的,由下式给出:

物理代考Gravity and Curvature of Space-Time 代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程