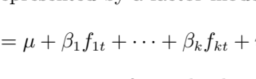数学代写| Arithmetic and Geometric Series 离散代考
离散数学在计算领域有广泛的应用,例如密码学、编码理论、 形式方法, 语言理论, 可计算性, 人工智能, 理论 数据库和软件的可靠性。 离散数学的重点是理论和应用,而不是为了数学本身而研究数学。 一切算法的基础都是离散数学一切加密的理论基础都是离散数学
编程时候很多奇怪的小技巧(特别是所有和位计算相关的东西)核心也是离散数学
其他相关科目课程代写:组合学Combinatorics集合论Set Theory概率论Probability组合生物学Combinatorial Biology组合化学Combinatorial Chemistry组合数据分析Combinatorial Data Analysis
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
离散数学代写
An arithmetic series is the sum of the terms in an arithmetic sequence, and geometric sequence is the sum of the terms in a geometric sequence. It is possible t derive a simple formula for the sum of the first $n$ terms in arithmetic and geometri series.
Arithmetic Series
We write the series in two ways: first, the normal left to right addition, and then th reverse, and then we add both series together:
$$
\begin{aligned}
&S n=a+(a+d)+(a+2 d)+(a+3 d)+\cdots+(a+(n-1) d) \
&S n=a+(n-1) d+a+(n-2) d+\cdots++(a+d)+a
\end{aligned}
$$
$S n=a+(a+d)+(a+2 d)+(a+3 d)+\cdots+(a+(n-1) d)$ $S n=a+(n-1) d+a+(n-2) d+\cdots+\quad+(a+d)+a$ $\cdots \cdot \cdots+(2 a+(n-1) d]+\cdots+[2 a+(n-1) d] \quad(n$ times $)$ $2 S n=[2 a+(n-1) d]+[(n-1) d]$ $2 S n=n \times[2 a+(-\cdots$ $2 S n=n \times[2 a+(n-1) d] .$
Therefore, we conclude that (where $r \neq 1$ )
$$
S_{n}=\frac{a\left(r^{n}-1\right)}{r-1}=\frac{a\left(1-r^{n}\right)}{1-r} .
$$
The case when $r=1$ corresponds to the arithmetic series $a+a+\cdots+a$, an the sum of this series is simply na. The geometric series converges when $|r|<1$ a $r^{n} \rightarrow 0$ as $n \rightarrow \propto$, and so
$$
S_{n} \rightarrow \frac{a}{1-r} \quad \text { as } n \rightarrow \infty
$$
Example (Geometric Series)
Find the sum of the first $n$ terms in the following geometric series $1,1 / 2,1 / 4,1 / 8, \ldots$ What is the sum of the series?
Solution
Clearly, $a=1$ and $r=1 / 2$. Therefore, applying the formula, we get

等差数列是等差数列中各项的和,等比数列是等比数列中各项的和。可以推导出算术和几何级数中前 $n$ 项之和的简单公式。
算术系列
我们以两种方式编写系列:首先,正常的从左到右相加,然后反向,然后我们将两个系列相加:
$$
\开始{对齐}
&S n=a+(a+d)+(a+2 d)+(a+3 d)+\cdots+(a+(n-1) d) \
&S n=a+(n-1) d+a+(n-2) d+\cdots++(a+d)+a
\end{对齐}
$$
$S n=a+(a+d)+(a+2 d)+(a+3 d)+\cdots+(a+(n-1) d)$ $S n=a+(n-1) d+a+ (n-2) d+\cdots+\quad+(a+d)+a$ $\cdots \cdot \cdots+(2 a+(n-1) d]+\cdots+[2 a+(n-1) d] \quad (n$ 次 $)$ $2 S n=[2 a+(n-1) d]+[(n-1) d]$ $2 S n=n \times[2 a+(-\cdots$ $2 S n= n \times[2 a+(n-1) d] .$
因此,我们得出结论(其中 $r \neq 1$ )
$$
S_{n}=\frac{a\left(r^{n}-1\right)}{r-1}=\frac{a\left(1-r^{n}\right)}{1- r} 。
$$
$r=1$ 对应算术级数$a+a+\cdots+a$ 的情况,这个级数的和就是na。当 $|r|<1$ a $r^{n} \rightarrow 0$ as $n \rightarrow \propto$ 时,几何级数收敛,依此类推
$$
S_{n} \rightarrow \frac{a}{1-r} \quad \text { as } n \rightarrow \infty
$$
示例(几何系列)
求下列几何级数 $1,1 / 2,1 / 4,1 / 8 中前 $n$ 项的和,\ldots$ 系列的和是多少?
解决方案
显然,$a=1$ 和 $r=1 / 2$。因此,应用公式,我们得到
图论代考
数学中使用的一些函数(或对象)(例如斐波那契数列)是
难以明确定义,最好由递归关系定义:即
递归定义一系列值的方程,一旦一个或多个初始值
值被定义。递归可用于定义函数、序列和
套。
递归定义有两个部分,即基本情况和
递归(归纳)步骤。基本情况通常定义函数的值
$n=0$ 或 $n=1$,而递归步骤指定如何应用
一个数的函数可以从其应用到一个或多个更小的函数中获得
数字。重要的是要注意递归定义,以确保它
不是循环的,也不会导致无限回归。函数的参数
递归步骤中定义的右侧通常小于
左侧的参数以确保终止(有一些不寻常的
递归定义的函数,例如 McCarthy 91 函数,其中 this 不是
案子)。当出现递归定义时,很自然地会问它是否意味着
任何东西,在某些情况下答案是否定的。不动点理论
为递归提供数学基础,并确保
功能/对象定义明确。
第 12 章(第 12.6 节)讨论了各种数学结构,例如偏
阶、完全偏阶和格,可用于给出
为递归奠定坚实的基础。给出了精确的数学含义
根据域和不动点理论递归定义的函数,它是
重要的是可以使用递归的条件
更多详细信息请参阅 [1]。
递归定义将包括至少一个非递归分支,每个递归分支都发生在与原始分支不同的上下文中,并带来
它更接近非递归情况。递归定义是一种强大而优雅的
给出语言结构的指称语义的方法。
接下来,我们给出阶乘函数 $\mathrm{~ N e x t i v i n g ~ d e n t i o n t}$ 的递归定义的例子
和斐波那契数。
例 4.4(函数的递归定义)阶乘函数 $n !$ 非常
在数学中很常见,其著名的定义是 $n !=$
$n(n-1)(n-2) \ldots 3.2 .1$ 和 $0 !=1$。根据基本情况的正式定义
归纳步骤如下:
$\begin{array}{ll}\text { 基本步骤 } & \text { fac }(0)=1 \ \text { 递归步骤 } & \text { fac }(n)=n * \operatorname{fac }(n-1)\end{数组}$
数学中使用的一些函数(或对象)(例如斐波那契数列)是
难以明确定义,最好由递归关系定义:即
递归定义一系列值的方程,一旦一个或多个初始值
值被定义。递归可用于定义函数、序列和
套。
递归定义有两个部分,即基本情况和
递归(归纳)步骤。基本情况通常定义函数的值
$n=0$ 或 $n=1$,而递归步骤指定如何应用
一个数的函数可以从其应用到一个或多个更小的函数中获得
数字。
重要的是要注意递归定义,以确保它
不是循环的,也不会导致无限回归。函数的参数
递归步骤中定义的右侧通常小于
左侧的参数以确保终止(有一些不寻常的
递归定义的函数,例如 $M c$ Carthy 91 函数,其中 this 不是
案子)。
当出现递归定义时,很自然地会问它是否意味着
任何东西,在某些情况下答案是否定的。不动点理论
为递归提供数学基础,并确保
功能/对象定义明确。
第 12 章(Sect. $12.6$)讨论了各种数学结构,例如偏
阶、完全偏阶和格,可用于给出
为递归奠定坚实的基础。给出了精确的数学含义
根据域和不动点理论递归定义的函数,它是
理解可以安全使用递归的条件至关重要。
$\mathrm{~ T h e ~ r e a d e r ~ i s ~ r e f e r}$
这个递归定义定义了一个数字的阶乘的过程
由基本情况确定,或由数字乘以的阶乘确定

数学代写| DISCRETE MATHEMATICS代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
抽象代数代考
抽象代数就是一门概念繁杂的学科,我们最重要的一点我想并不是掌握多少例子。即便是数学工作者也不会刻意记住Jacobson环、正则环这类东西,重要的是你要知道这门学科的基本工具和基本手法,对概念理解了没有,而这一点不需要用例子来验证,只需要看看你的理解和后续概念是否相容即可。
矩阵论代考matrix theory
数学,矩阵理论是一门研究矩阵在数学上的应用的科目。矩阵理论本来是线性代数的一个小分支,但其后由于陆续在图论、代数、组合数学和统计上得到应用,渐渐发展成为一门独立的学科。
密码学代考
密码学是研究编制密码和破译密码的技术科学。 研究密码变化的客观规律,应用于编制密码以保守通信秘密的,称为编码学;应用于破译密码以获取通信情报的,称为破译学,总称密码学。 电报最早是由美国的摩尔斯在1844年发明的,故也被叫做摩尔斯电码。
- Cryptosystem
- A system that describes how to encrypt or decrypt messages
- Plaintext
- Message in its original form
- Ciphertext
- Message in its encrypted form
- Cryptographer
- Invents encryption algorithms
- Cryptanalyst
- Breaks encryption algorithms or implementations
编码理论代写
编码理论(英语:Coding theory)是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错,最近也用于网络编码中。不同学科(如信息论、电机工程学、数学、语言学以及计算机科学)都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正(或检测)数据传输中的错误。
编码共分四类:[1]
数据压缩和前向错误更正可以一起考虑。