数学代写| Other Changes: Drawbacks of the Graphical Methods 凸优化代考
凸优化代写
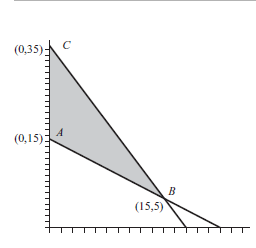
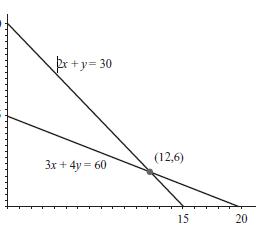
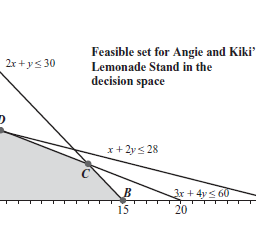
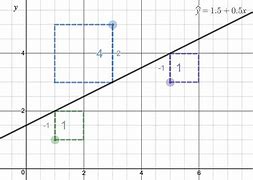
We have observed that marginal values are a local phenomenon, meaning that they remain valid for a range of values as we change the number in the right-hand side of the relevant constraint. A large change in this number, going outside this range, will result in a more drastic change. To see what kind of change, consider again the lemonade stand problem with its optimal solution at point $C$ in the graph of the feasible set in Figure 4.1.
In computing the marginal value of a lemon, we increased the lemons supply from 60 to 61 , which had the effect on the graph of moving the line for the lemon constraint slightly farther away from the origin. The new position of this line is parallel to the one in Figure 4.1, because the slope does not change when we increase the lemon supply to 61 . If the reader visualizes what happens to this line as we increase lemons even further, we have already observed that the coordinates of the optimal point $C$ change slightly (as do the coordinates of the non-optimal point $D$ ). Let’s call the (infeasible) point of intersection of the lime line and the sugar line $F$. The modified point for the modified point $D$ also moves to the right along the lime line toward $F$.
At some point, if we increase the supply of lemons enough, the modified lemon constraint line will pass through $F$ (and points $C$ and $D$ converge to and become coincident with $F$.) At this level of lemon supply, since all three lines pass though the same point $F$, the problem is degenerate. But more importantly, think of what happens if we increase the lemon supply further. If we keep moving the lemon line past this point, it completely misses the feasible set – that is, it become superfluous. This is because we have run out of the other two resources, so additional lemons no longer help. Thus, the optimal point would remain at point $F$, and the optimal solution will have slackness that at this point, the marginal value of a lemon suddenly becomes 0 . Another way to say it is that the optimal point $F$ has a different set of basic variables than does the point $C$ because $S_{1}>0$ and now $S_{2}=0$. (Basic variables were defined in Section 3.5.)
Similar reasoning applies if we lower the supply of lemons. The lemon constraint line now moves slowly toward the origin, and the points $C$ and $D$ move away from $F$ instead of toward it. In particular, the point $C$ moves down the segment $B F$ toward $B$ on the sugar line. As soon as this line hits point $B$, the problem degenerates, and any further lowering of the supply of lemons the marginal value of a lemon. This leads us to Definition $4.5$.
DEFINITION $4.5$ For each constraint, the stable range of the capacity number (the value of the right-hand side of the constraint) is the range of values for which the marginal value associated with that constraint is unchanged. Equivalently, it is the range of values for which the basic variables in the optimal solution are unchanged.
Clearly, we can find the range as follows. We know the equation of any line parallel to the lemon constraint line has equation
$$
3 x+4 y=d \text {. }
$$
As long as $d$ is chosen so that the point $C$ lies between $B$ and $F$ on the sugar line, then the basic variables of the optimal solution are unchanged. For this line to pass through $B$, we substitute in the coordinates of $B$ into this line:
$$
\begin{aligned}
3(15)+4(0) &=d \
45 &=d
\end{aligned}
$$
4.4 Other Changes
Similarly, for this line to pass through $F$, we would substitute the coordinates of $F$ into this line. Although we have not previously computed the coordinates of $F$, the reader should verify that the coordinates are $\left(\frac{32}{3}, \frac{26}{3}\right)$, lime line and the sugar line. Thus,
$3\left(\frac{32}{3}\right)+4\left(\frac{26}{3}\right)=d$
$$
\frac{200}{3}=d \text {. }
$$
Thus, we have found the stable range for $d$ :
$45 \leq d \leq \frac{200}{3}=66 \frac{2}{3}$. The conclusion is that as long as the supply of lemons is between 45 and $\frac{200}{3}$, then the optinal point has the same basic variables as point $C$ (namely, $x, y$, and $S_{2}$ ), and the marginal value of a lemon calculated in the last section, $\$ 0.35$, is valid throughout this range. If the supply of lemons exceeds $\frac{200}{3}$, then $S_{1}$ becomes a basic variable (and $M_{1}$ changes to 0 ). If the supply of lemons drops below 45 , then again the basic variables change. In this case, $y$ becomes nonbasic, and both $S_{2}$ and $S_{3}$ become basic because both limes and sugar are left over at the modified point $B$. Again, leftover lemons. We leave it to the reader to find what it changes to if $d<45$.
Similar reasoning can be applied to find the stable range for sugar. This time it is the sugar line that moves, and point $C$ moves along the segment of the lemon line connecting point $D$ to the (unlabeled) point $(20,0)$ on the $x$-axis. Any line parallel to the sugar line has equation
$$
2 x+y=d
$$
To pass through $D$, we must have
凸优化代考
我们观察到边际值是一种局部现象,这意味着当我们更改相关约束右侧的数字时,它们对于一系列值仍然有效。这个数字的大变化,超出这个范围,将导致更剧烈的变化。要查看什么样的变化,请再次考虑柠檬水摊问题及其在图 4.1 中可行集图中的点 $C$ 处的最优解。
在计算柠檬的边际价值时,我们将柠檬供应量从 60 增加到 61 ,这对将柠檬约束线稍微远离原点的图产生了影响。这条线的新位置与图 4.1 中的位置平行,因为当我们将柠檬供应量增加到 61 时,斜率不会改变。如果读者想象当我们进一步增加柠檬时这条线会发生什么,我们已经观察到最佳点 $C$ 的坐标略有变化(非最佳点 $D$ 的坐标也是如此)。让我们将石灰线和糖线的(不可行的)交点称为 $F$。修改点$D$ 的修改点也沿石灰线向右移动到$F$。
在某个时刻,如果我们足够增加柠檬的供应量,修改后的柠檬约束线将通过 $F$(并且点 $C$ 和 $D$ 会聚并与 $F$ 重合。)在这个柠檬水平供应,因为所有三条线都通过同一个点 $F$,所以问题是退化的。但更重要的是,想想如果我们进一步增加柠檬供应会发生什么。如果我们继续将柠檬线移过这一点,它就完全错过了可行集——也就是说,它变得多余了。这是因为我们已经用完了其他两种资源,所以额外的柠檬不再有帮助。因此,最优点将保持在点 $F$,并且最优解将具有松弛性,在这一点上,柠檬的边际值突然变为 0。另一种说法是,最优点 $F$ 具有与点 $C$ 不同的一组基本变量,因为 $S_{1}>0$ 并且现在 $S_{2}=0$。 (基本变量在第 3.5 节中定义。)
如果我们减少柠檬的供应,类似的推理也适用。柠檬约束线现在缓慢地向原点移动,点 $C$ 和 $D$ 远离 $F$ 而不是向它移动。特别是,$C$ 点沿 $B F$ 段向下移动,向糖线上的 $B$ 移动。一旦这条线达到$B$,问题就会退化,柠檬供应的任何进一步降低都会影响柠檬的边际价值。这将我们引向定义 $4.5$。
定义 $4.5$ 对于每个约束,容量数的稳定范围(约束右侧的值)是与该约束相关的边际值不变的值的范围。等效地,它是最优解中基本变量不变的值的范围。
显然,我们可以找到如下范围。我们知道任何平行于柠檬约束线的线的方程都有方程
$$
3 x+4 y=d \text {。 }
$$
只要选择$d$ 使得$C$ 位于糖线上的$B$ 和$F$ 之间,那么最优解的基本变量不变。为了让这条线穿过 $B$,我们将 $B$ 的坐标代入这条线:
$$
\开始{对齐}
3(15)+4(0) &=d \
45 &=d
\end{对齐}
$$
4.4 其他变化
类似地,为了让这条线穿过 $F$,我们将把 $F$ 的坐标代入这条线。虽然我们之前没有计算过 $F$ 的坐标,但读者应该验证坐标是 $\left(\frac{32}{3}, \frac{26}{3}\right)$、lime line 和糖线。因此,
$3\left(\frac{32}{3}\right)+4\left(\frac{26}{3}\right)=d$
$$
\frac{200}{3}=d \text {。 }
$$
因此,我们找到了 $d$ 的稳定范围:
$45 \leq d \leq \frac{200}{3}=66 \frac{2}{3}$。结论是,只要柠檬的供应量在 45 和 $\frac{200}{3}$ 之间,那么最优点与点 $C$ 具有相同的基本变量(即 $x、y$ 和$S_{2}$ ),并且在最后一节中计算的柠檬的边际价值 $\$ 0.35$ 在整个范围内都有效。如果柠檬的供应量超过 $\frac{200}{3}$,则 $S_{1}$ 成为基本变量($M_{1}$ 变为 0)。如果柠檬的供应量下降到 45 以下,那么基本变量会再次发生变化。在这种情况下,$y$ 变为非基本的,$S_{2}$ 和 $S_{3}$ 都变为基本的,因为在修改的点 $B$ 处留下了酸橙和糖。再一次,剩下的柠檬。如果 $d<45$,我们将其留给读者去寻找它的变化。
可以应用类似的推理来找到糖的稳定范围。这次是糖线移动,点 $C$ 沿着连接点 $D$ 到 $x$ 轴上(未标记的)点 $(20,0)$ 的柠檬线段移动。任何平行于糖线的线都有方程
$$
2 x+y=d
$$
要通过$D$,我们必须

数学代写| Chebyshev polynomials 数值分析代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
时间序列分析代写
统计作业代写
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程