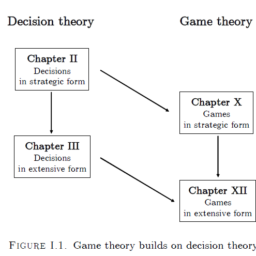
经济代写|The macroeconomy as a web of flows 宏观经济学代写
经济代写
2.4 The macroeconomy as a web of flows
We discussed the three ways of conceptualising the economy in Section 2.1. They àrè NIA, I-O méthỏd, and FoF analysis. Thẻ látteer two togeether, particularly, aid our understanding of contemporary economies, which are monetary production economies. And in Section 2.3, we pointed out the scope of economics in relation to the divergent views between economists’ wishes for the community and the wishes of that community and the boundaries presented by the social and ecological systems. In this section, we visualise the macroeconomy as a web of commodity and money flows.
An early representation of this, as noted earlier, is found in Quesnay’s Tableau Économique – a zig-zag of value-sums travelling across the proprietary, agricultural and manufacturing classes. For you to appreciate Quesnay’s work better and to get a flavour of his conceptualisation, I present an abstract from his Tableau Économique.
31
MACROECONOMICS
The 300 livres of revenue which have passed into the hands of the [manufacturing] class are spent by the artisan, as to one-half, in the purchase of products for his subsistence, for raw materials for his work, and for foreign trade, from the [agricultural] class; and the other half is distributed among the [manufacturing] class itself for its maintenance and for the redistribution of its advances. This circulation and mutual distribution are combined in the same way by means of sub-divisions down to the last penny of the sums of money which mutuin. (pp. ii-iii)
From Quesnay’s conceptualisation, it is clear that to study the macro economy (and mẻsó économy), we neeed tó examiné sẻctoral flows. Thè sèctors could be agriculture, manufacturing or services as in IOTT or households, private corporate business or government as in FoF.
Marx, writing 100 years after Quesnay, also possessed a depiction of commodity and money flows: $M-C-C^{\prime}-M^{\prime}$. In a canpitalist socièty, thé capitalists, who are the owners of the means of production, exchange money (M) for commodities (C). Workers are employed to increase the value of $\mathrm{C}$ to $\mathrm{C}^{\prime}$; the difference between $\mathrm{C}^{\prime}$ and $\mathrm{C}$ is owing to the value added by the workers. If all of $\mathrm{C}^{\prime}$ is sold (or exchanged for money) in the market, the capitalists obtain $\mathrm{M}^{\prime}$, a sum of money greater than $\mathrm{M}$. We can identify three phases in the above “general formula for capital”, as Marx calls it. The M-C. is the investment phase, $\mathrm{C}-\mathrm{C}^{\prime}$ the production phase where value gets added, and $\mathrm{C}^{\prime}-\mathrm{M}^{\prime}$ the consumption (or selling or exchange) phase. If a disruption occurs in the selling phase, the capitalists need not obtain their advances or investment back, and the circular flow in the economy is disrupted. In other words, if there are inadequate sales, insufficient profits are made and the the circular flow).
Roughly another century later, Piero Sraffa, in his 1960 book Production of Commodities by Means of Commodities, credits Quesnay’s Tableau Économique for containing “the original picture of the system of production and consumption as a circular process” (p. 93). Contemporary research in economics, which follows the classical tradition of Smith, Ricardo and others, is indebted to Sraffa’s book, which revived the tradition of classical political economy. In Quesnay, Marx and Sraffa, we also find meso approaches to studying the economy.
It is now time to list the key sectors in our conceptualisation of the Indian macroeconomy. In order to study the commodity and money flows, we divide
32
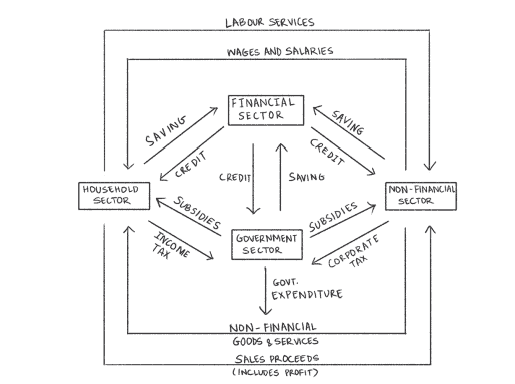
2.4 作为流量网络的宏观经济
我们在第 2.1 节中讨论了经济概念化的三种方式。他们采用 NIA、I-O 方法和 FoF 分析。这两节课特别有助于我们理解当代经济,即货币生产经济。在第 2.3 节中,我们指出了与经济学家对社区的愿望和社区的愿望之间的分歧观点以及社会和生态系统所呈现的界限有关的经济学范围。在本节中,我们将宏观经济可视化为商品和资金流动的网络。
如前所述,在 Quesnay 的 Tableau Économique 中发现了这一点的早期表现——价值总和在专有、农业和制造业类别中的曲折。为了让您更好地欣赏 Quesnay 的作品并了解他的概念化,我提供了他的 Tableau Économique 的摘要。
31
宏观经济
手工业者手中的 300 里弗收入,其中一半用于购买生活所需的产品、工作的原材料和对外贸易,来自[农业]阶级;另一半则分配给[制造业]阶级本身,用于维护和重新分配其预付款。这种流通和相互分配以同样的方式结合起来,通过细分到货币总额的最后一分钱。 (第 ii-iii 页)
从 Quesnay 的概念化来看,很明显,要研究宏观经济(和 mẻsó 经济),我们需要检查部门流动。这些部门可以是 IOTT 中的农业、制造业或服务业,也可以是家庭、私营企业或 FoF 中的政府部门。
马克思在 Quesnay 之后 100 年写作,也对商品和货币流动进行了描述:$M-C-C^{\prime}-M^{\prime}$。在资本主义社会中,作为生产资料所有者的资本家用货币(M)交换商品(C)。雇佣工人将$\mathrm{C}$的价值增加到$\mathrm{C}^{\prime}$; $\mathrm{C}^{\prime}$ 和 $\mathrm{C}$ 之间的差异是由于工人增加的价值。如果 $\mathrm{C}^{\prime}$ 全部在市场上出售(或兑换成货币),则资本家获得 $\mathrm{M}^{\prime}$,这是一笔大于 $ \mathrm{M}$。正如马克思所说,我们可以在上述“资本的一般公式”中确定三个阶段。 M-C。是投资阶段,$\mathrm{C}-\mathrm{C}^{\prime}$ 是增值的生产阶段,$\mathrm{C}^{\prime}-\mathrm{M}^ {\prime}$ 消费(或销售或交换)阶段。如果在销售阶段发生中断,资本家不需要收回他们的预付款或投资,经济中的循环流动就会被打乱。换句话说,如果销售不足,则利润不足,循环流动)。
大约又过了一个世纪,皮耶罗·斯拉法(Piero Sraffa)在他 1960 年的著作《通过商品生产商品》中称赞 Quesnay 的经济表包含“作为循环过程的生产和消费系统的原始图景”(第 93 页)。当代经济学研究沿袭了斯密、李嘉图等人的古典传统,这要归功于斯拉法的著作,它复兴了古典政治经济学的传统。在 Quesnay、Marx 和 Sraffa,我们还发现了研究经济的中观方法。
现在是时候列出我们对印度宏观经济概念化的关键部门了。为了研究商品和货币流动,我们划分
32
经济代考
宏观经济学,是以国民经济总过程的活动为研究对象,主要考察就业总水平、国民总收入等经济总量,因此,宏观经济学也被称做就业理论或收入理论。 宏观经济学研究的是经济资源的利用问题,包括国民收入决定理论、就业理论、通货膨胀理论、经济周期理论、经济增长理论、财政与货币政策。

其他相关科目课程代写:组合学Combinatorics集合论Set Theory概率论Probability组合生物学Combinatorial Biology组合化学Combinatorial Chemistry组合数据分析Combinatorial Data Analysis
my-assignmentexpert愿做同学们坚强的后盾,助同学们顺利完成学业,同学们如果在学业上遇到任何问题,请联系my-assignmentexpert™,我们随时为您服务!
宏观经济学是经济学的一个分支,它研究的是一个整体经济,即市场或其他大规模运作的系统是如何运作的。宏观经济学研究经济范围内的现象,如通货膨胀价格水平经济增长,国民收入,国内生产总值,以及失业 .
计量经济学代考
计量经济学是以一定的经济理论和统计资料为基础,运用数学、统计学方法与电脑技术,以建立经济计量模型为主要手段,定量分析研究具有随机性特性的经济变量关系的一门经济学学科。 主要内容包括理论计量经济学和应用经济计量学。 理论经济计量学主要研究如何运用、改造和发展数理统计的方法,使之成为经济关系测定的特殊方法。
相对论代考
相对论(英語:Theory of relativity)是关于时空和引力的理论,主要由愛因斯坦创立,依其研究对象的不同可分为狭义相对论和广义相对论。 相对论和量子力学的提出给物理学带来了革命性的变化,它们共同奠定了现代物理学的基础。
编码理论代写
编码理论(英语:Coding theory)是研究编码的性质以及它们在具体应用中的性能的理论。编码用于数据压缩、加密、纠错,最近也用于网络编码中。不同学科(如信息论、电机工程学、数学、语言学以及计算机科学)都研究编码是为了设计出高效、可靠的数据传输方法。这通常需要去除冗余并校正(或检测)数据传输中的错误。
编码共分四类:[1]
数据压缩和前向错误更正可以一起考虑。
复分析代考
学习易分析也已经很冬年了,七七八人的也续了圧少的书籍和论文。略作总结工作,方便后来人学 Đ参考。
复分析是一门历史悠久的学科,主要是研究解析函数,亚纯函数在复球面的性质。下面一昭这 些基本内容。
(1) 提到复变函数 ,首先需要了解复数的基本性左和四则运算规则。怎么样计算复数的平方根, 极坐标与 $x y$ 坐标的转换,复数的模之类的。这些在高中的时候囸本上都会学过。
(2) 复变函数自然是在复平面上来研究问题,此时数学分析里面的求导数之尖的运算就会很自然的 引入到复平面里面,从而引出解析函数的定义。那/研究解析函数的性贡就是关楗所在。最关键的 地方就是所谓的Cauchy一Riemann公式,这个是判断一个函数是否是解析函数的关键所在。
(3) 明白解析函数的定义以及性质之后,就会把数学分析里面的曲线积分 $a$ 的概念引入复分析中, 定义几乎是一致的。在引入了闭曲线和曲线积分之后,就会有出现复分析中的重要的定理: Cauchy 积分公式。 这个是易分析的第一个重要定理。