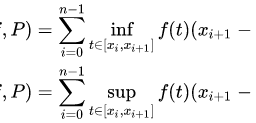微积分(Calculus),数学概念,是高等数学中研究函数的微分(Differentiation)、积分(Integration)以及有关概念和应用的数学分支。它是数学的一个基础学科,内容主要包括极限、微分学、积分学及其应用。微分学包括求导数的运算,是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。积分学,包括求积分的运算,为定义和计算面积、体积等提供一套通用的方法
my-assignmentexpert™ 微积分calculus作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的微积分calculus作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于economics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此微积分calculus作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在经济学作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的微积分calculus代写服务。我们的专家在微积分calculus学 代写方面经验极为丰富,各种微积分calculus相关的作业也就用不着 说。
我们提供的econ代写服务范围广, 其中包括但不限于:
- 单变量微积分
- 多变量微积分
- 傅里叶级数
- 黎曼积分
- ODE
- 微分学

微积分代考calculus代写|convergent sequence
First we need to define what is meant by finite total variation.
CHAPTER 9. INTEGRATION
186
Definition 9.3.1 Let $g$ be an arbitrary function defined on $[a, b] .$ For $P_{[a, x]} \equiv$ $\left{x_{0}, \cdots, x_{n}\right}$ a partition of $[a, x]$, define $V\left(P_{[a, x]}, g\right)$ by
$$
\sum_{i=1}^{n}\left|g\left(x_{i}\right)-g\left(x_{i-1}\right)\right|
$$
Define the total variation of $g$ on $[a, x]$ by
$$
V_{[a, x]}(g) \equiv \sup \left{V\left(P_{[a, x]}, g\right): P_{[a, x]} \text { is a partition of }[a, x]\right} .
$$
Then $g$ is said to be of bounded variation on $[a, b]$ if $V_{[a, b]}(g)$ is finite. Also, for $P=$ $\left{x_{0}, x_{1}, \cdots, x_{n}\right}$ where $x_{k} \geq x_{k-1},|P| \equiv \max \left{\left|x_{k}-x_{k-1}\right|: k=1,2, \cdots, n\right}$.
Then with this definition, one has an important proposition which pertains to the case of principal interest here in which the functions are all real valued. The above definition of finite total variation works for functions which have values in some normed linear space however.
Proposition $9.3 .2$ Every real valued function $g$ of bounded variation can be written as the difference of two increasing function, one of which is the function $x \rightarrow V_{[a, x]}(g)$. Furthermore, the functions of bounded variation are exactly those functions which are the difference of two increasing functions.
Proof: Let $g$ be of bounded variation. It is obvious from the definition that $x \rightarrow$ $V_{[a, x]}(g)$ is an increasing function. Also $g(x)=V_{[a, x]}(g)-\left(V_{[a, x]}(g)-g(x)\right)$ The first part of the proposition is proved if I can show $x \rightarrow V_{[a, x]}(g)-g(x)$ is increasing. Let $x \leq y$. Is it true that $V_{[a, x]}(g)-g(x) \leq V_{[a, y]}(g)-g(y) ?$ This is true if and only if
$$
g(y)-g(x) \leq V_{[a, y]}(g)-V_{[a, x]}(g)
$$
To show this is so, first note that $V\left(P_{[a, x]}, g\right) \leq V\left(Q_{[a, x]}, g\right)$ whenever the partition $Q_{[a, x]} \supseteq P_{[a, x]}$. You demonstrate this by adding in one point at a time and using the triangle inequality. Now let $P_{y}$ and $P_{[a, x]}$ be partitions of $[a, y]$ and $[a, x]$ respectively such that
$$
V\left(P_{[a, x]}, g\right)+\varepsilon>V_{[a, x]}(g), V\left(P_{y}, g\right)+\varepsilon>V_{[a, y]}(g)
$$
Without loss of generality $P_{y}$ contains $x$ because from what was just shown you could add in the point $x$ and the approximation of $V\left(P_{y}, g\right)$ to $V_{[a, y]}(g)$ would only be better. Then from the definition,
$$
\begin{gathered}
V_{[a, y]}(g)-V_{[a, x]}(g) \geq V\left(P_{y}, g\right)-\left(V\left(P_{[a, x]}, g\right)+\varepsilon\right) \
\geq|g(y)-g(x)|-\varepsilon \geq g(y)-g(x)-\varepsilon
\end{gathered}
$$
微积分代考CALCULUS代写|divergent sequence
and since $\varepsilon$ is arbitrary, this establishes $9.3$. This proves the first part of the proposition.
Now suppose $g(x)=g_{1}(x)-g_{2}(x)$ where each $g_{i}$ is an increasing function. Why is $g$ of bounded variation? Letting $x0$, there exists $\delta>0$ such that if
$$
P \equiv\left{x_{0}, x_{1}, \cdots, x_{n}\right}, a=x_{0}<\cdots<x_{n}=b
$$
is any partition hoving $|P|<\delta$, and $z_{i} \in\left[x_{i-1}, x_{i}\right]$,
$$
\left|I-\sum_{i=1}^{n} f\left(z_{i}\right)\left(g\left(x_{i}\right)-g\left(x_{i-1}\right)\right)\right|<\varepsilon .
$$
The number $\int_{a}^{b} f(x) d g(x)$ is defined as 1 . I will denote this Riemann Stieltjes sum approximating I as $\sum_{P} f\left(z_{i}\right)\left(g\left(x_{i}\right)-g\left(x_{i-1}\right)\right)$. When $f$ is Riemann Stieltjes integrable on $[a, b]$ with respect to $g$ as just described, this is denoted as $f \in R([a, b], g)$ or simply as $R[a, b]$ if the definition is clear for $g$.
A special case is the following definition.
Definition 9.3.4 The Riemann integral is a special case of the above in which $g(x)=x$. We write $\int_{a}^{b} f(x) d g(x)$ in the form $\int_{a}^{b} f(x) d x$ to signify the Riemann integral.
There is only one possible number $I$ satisfying the above definition.
Lemma 9.3.5 The integral $\int_{a}^{b} f(x) d g(x)$ is well defined in the sense that if there is such a number $I$, then there is only one.
Proof: Suppose you have two of them $I, \hat{I}$ and that $P, \hat{P}$ are corresponding partitions such that $|P|,|\hat{P}|$ are both small enough that
$$
\left|I-\sum_{P} f\left(z_{i}\right)\left(g\left(x_{i}\right)-g\left(x_{i-1}\right)\right)\right|<\varepsilon,\left|\hat{I}-\sum_{\hat{P}} f\left(\hat{z}{i}\right)\left(g\left(x{i}\right)-g\left(x_{i-1}\right)\right)\right|<\varepsilon
$$
whenever $z_{i}$ or $\hat{z}{i}$ are in $\left[x{i-1}, x_{i}\right]$. Let $Q \equiv P \cup \hat{P}$ and choose $z_{i}$ and $\hat{z}{i}$ to be the left endpoint of the sub intervals defined by the partition $Q$. Then $|Q| \leq \min (|P|,|\hat{P}|)$ and so $|I-S|<\varepsilon,|\hat{I}-S|<\varepsilon$ where $S=\sum{Q} f\left(x_{i-1}\right)\left(g\left(x_{i}\right)-g\left(x_{i-1}\right)\right)$. Then $|I-\hat{I}| \leq|I-S|+|S-\hat{I}|<2 \varepsilon$. Since $\varepsilon$ is arbitrary, $I=\hat{I}$.
Next is a fairly obvious theorem which says essentially that things which hold for sums typically hold for integrals also, provided the integrals exist.
Theorem 9.3.6 Assuming all integrals make sense, the following relation exists for $f, g$ functions and $a, b$ scalars.
$$
\int_{a}^{b}(a f+b \hat{f}) d g=a \int_{a}^{b} f d g+b \int_{a}^{b} \hat{f} d g
$$
Assuming all integrals make sense and $g$ is increasing, it follows that
$$
\int_{a}^{b}|f| d g \geq\left|\int_{a}^{b} f d g\right|
$$
Also, if $a<c<b$ and all integrals make sense for $I=[a, c],[a, b],[c, b]$, then

微积分代考CALCULUS代写|CONVERGENT SEQUENCE
首先,我们需要定义有限总变异的含义。
第 9 章积分
186
定义 9.3.1 让G是定义在[一种,b].为了磷[一种,X]≡ \left{x_{0}, \cdots, x_{n}\right}\left{x_{0}, \cdots, x_{n}\right}一个分区[一种,X], 定义五(磷[一种,X],G)经过
∑一世=1n|G(X一世)−G(X一世−1)|
定义总变异G在[一种,X]经过
V_{[a, x]}(g) \equiv \sup \left{V\left(P_{[a, x]}, g\right): P_{[a, x]} \text { 是一个分区的 }[a, x]\right} 。V_{[a, x]}(g) \equiv \sup \left{V\left(P_{[a, x]}, g\right): P_{[a, x]} \text { 是一个分区的 }[a, x]\right} 。
然后G据说是有界变化的[一种,b]如果五[一种,b](G)是有限的。此外,对于磷= \left{x_{0}, x_{1}, \cdots, x_{n}\right}\left{x_{0}, x_{1}, \cdots, x_{n}\right}在哪里x_{k} \geq x_{k-1},|P| \equiv \max \left{\left|x_{k}-x_{k-1}\right|: k=1,2, \cdots, n\right}x_{k} \geq x_{k-1},|P| \equiv \max \left{\left|x_{k}-x_{k-1}\right|: k=1,2, \cdots, n\right}.
然后有了这个定义,我们就有了一个重要的命题,它与这里的主要利益情况有关,在这种情况下,函数都是实值的。然而,上述有限总变分的定义适用于在某些规范线性空间中具有值的函数。
主张9.3.2每个实值函数G有界变化的可以写成两个增函数的差,其中一个是函数X→五[一种,X](G). 此外,有界变分函数正是两个递增函数之差的函数。
证明:让G是有界变化的。从定义中可以看出X→ 五[一种,X](G)是一个递增函数。还G(X)=五[一种,X](G)−(五[一种,X](G)−G(X))如果我能证明命题的第一部分X→五[一种,X](G)−G(X)在增长。让X≤和. 是不是真的五[一种,X](G)−G(X)≤五[一种,和](G)−G(和)?这是真的当且仅当
G(和)−G(X)≤五[一种,和](G)−五[一种,X](G)
为了证明这一点,首先请注意五(磷[一种,X],G)≤五(问[一种,X],G)每当分区问[一种,X]⊇磷[一种,X]. 您可以通过一次添加一个点并使用三角不等式来证明这一点。现在让磷和和磷[一种,X]是的分区[一种,和]和[一种,X]分别使得
五(磷[一种,X],G)+e>五[一种,X](G),五(磷和,G)+e>五[一种,和](G)
不失一般性磷和包含X因为从刚刚显示的内容中,您可以添加这一点X和近似值五(磷和,G)到五[一种,和](G)只会更好。那么根据定义,
五[一种,和](G)−五[一种,X](G)≥五(磷和,G)−(五(磷[一种,X],G)+e) ≥|G(和)−G(X)|−e≥G(和)−G(X)−e
微积分代考CALCULUS代写|DIVERGENT SEQUENCE
并且因为e是任意的,这建立9.3. 这证明了命题的第一部分。
现在假设G(X)=G1(X)−G2(X)其中每个G一世是一个递增函数。为什么是G有界变化?让X0, 那里存在d>0这样如果
P \equiv\left{x_{0}, x_{1}, \cdots, x_{n}\right}, a=x_{0}<\cdots<x_{n}=bP \equiv\left{x_{0}, x_{1}, \cdots, x_{n}\right}, a=x_{0}<\cdots<x_{n}=b
是否有任何分区悬停|磷|<d, 和和一世∈[X一世−1,X一世],
|一世−∑一世=1nF(和一世)(G(X一世)−G(X一世−1))|<e.
号码∫一种bF(X)dG(X)定义为 1 。我将把这个近似于 I 的 Riemann Stieltjes 和表示为∑磷F(和一世)(G(X一世)−G(X一世−1)). 什么时候FRiemann Stieltjes 可积在[一种,b]关于G如前所述,这表示为F∈R([一种,b],G)或者简单地说R[一种,b]如果定义明确G.
一个特例是下面的定义。
定义 9.3.4 黎曼积分是上述的一个特例,其中G(X)=X. 我们写∫一种bF(X)dG(X)在表格中∫一种bF(X)dX来表示黎曼积分。
只有一个可能的数字一世满足上述定义。
引理 9.3.5 积分∫一种bF(X)dG(X)从某种意义上说,如果有这样一个数字,则定义良好一世,那么只有一个。
证明:假设你有两个一世,一世^然后磷,磷^是对应的分区,使得|磷|,|磷^|都足够小
$$
\left|I-\sum_{P} f\left(z_{i}\right)\left(g\left(x_{i}\right)-g\left(x_{i -1}\right)\right)\right|<\varepsilon,\left|\hat{I}-\sum_{\hat{P}} f\left(\hat{z} {i}\right)\左(g\left(x {i}\right)-g\left(x_{i-1}\right)\right)\right|<\varepsilon
$$
每当和一世或 $\hat{z} {i}一种r和一世n\left[x {i-1}, x_{i}\right].一世和吨Q \equiv P \cup \hat{P}一种ndCH○○s和z_ {i}一种nd\帽子{z} {i}吨○b和吨H和一世和F吨和ndp○一世n吨○F吨H和s你b一世n吨和rv一种一世sd和F一世n和db和吨H和p一种r吨一世吨一世○n问.吨H和n|问| \leq \min (|P|,|\hat{P}|)一种nds○|IS|<\varepsilon,|\hat{I}-S|<\varepsilon在H和r和S=\sum {Q} f\left(x_{i-1}\right)\left(g\left(x_{i}\right)-g\left(x_{i-1}\right)\right ).吨H和n|我-\帽子{我}| \leq|IS|+|S-\hat{I}|<2 \varepsilon.小号一世nC和\伐普西隆一世s一种rb一世吨r一种r和,我=\帽子{我}$。
接下来是一个相当明显的定理,它本质上说,只要积分存在,对总和成立的事物通常也对积分成立。
定理 9.3.6 假设所有积分都有意义,则存在以下关系F,G功能和一种,b标量。
∫一种b(一种F+bF^)dG=一种∫一种bFdG+b∫一种bF^dG
假设所有积分都有意义并且G正在增加,因此
∫一种b|F|dG≥|∫一种bFdG|
另外,如果一种<C<b并且所有积分对于一世=[一种,C],[一种,b],[C,b], 然后

微积分note Integer Multiples of Irrational Numbers 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。