如果你也在 怎样代写运筹学Operations Research这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。假设检验Hypothesis是假设检验是统计学中的一种行为,分析者据此检验有关人口参数的假设。分析师采用的方法取决于所用数据的性质和分析的原因。假设检验是通过使用样本数据来评估假设的合理性。
运筹学(Operation)是近代应用数学的一个分支。它把具体的问题进行数学抽象,然后用像是统计学、数学模型和算法等方法加以解决,以此来寻找复杂问题中的最佳或近似最佳的解答。
二战中运筹学的应用
在二战时期,作战研究被定义为 “一种科学方法,为执行部门提供有关其控制的行动的决策的量化依据”。它的其他名称包括作战分析(英国国防部从1962年开始)和定量管理。
在第二次世界大战期间,英国有近1000名男女从事作战研究。大约有200名作战研究科学家为英国军队工作。
帕特里克-布莱克特在战争期间为几个不同的组织工作。战争初期,在为皇家飞机研究所(RAE)工作时,他建立了一个被称为 “马戏团 “的团队,帮助减少了击落一架敌机所需的防空炮弹数量,从不列颠战役开始时的平均超过20,000发减少到1941年的4,000发。
my-assignmentexpert™ 运筹学Operations Research作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的运筹学Operations Research作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此运筹学Operations Research作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在运筹学Operations Research作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的应用数学applied math代写服务。我们的专家在运筹学Operations Research代写方面经验极为丰富,各种运筹学Operations Research相关的作业也就用不着 说。
我们提供的假设检验Hypothesis及其相关学科的代写,服务范围广, 其中包括但不限于:
- 商业分析 Business Analysis
- 计算机科学 Computer Science
- 数据挖掘/数据科学/大数据 Data Mining / Data Science / Big Data
- 决策分析 Decision Analytics
- 金融工程 Financial Engineering
- 数据预测 Data Forecasting
- 博弈论 Game Theory
- 地理/地理信息科学 Geography/Geographic Information Science
- 图论 Graph Theory
- 工业工程 Industrial Engineering
- 库存控制 Inventory control
- 数学建模 Mathematical Modeling
- 数学优化 Mathematical Optimization
- 概率和统计 Probability and statistics
- 排队论 Queueing theory
- 社交网络/交通预测模型 Social network/traffic prediction modeling
- 随机过程 Stochastic processes
- 供应链管理 Supply chain management
运筹学代写
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|Woodland biomass PoWeR (us)
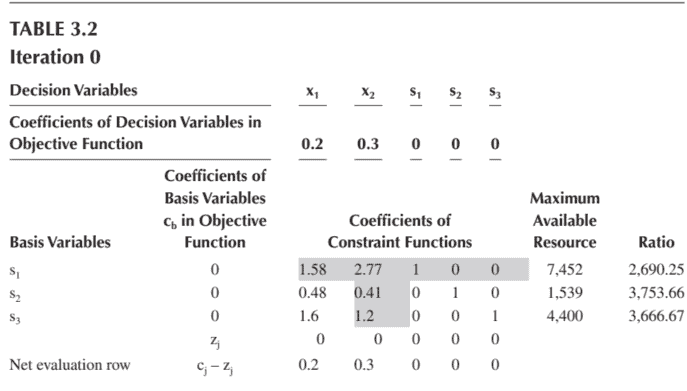
The simplex method requires the following steps for solving a linear programming problem (LPP).
Step 1: Model Construction
The case clearly illustrates that the amount of fuel A and B are variables which would decide the profit of a company. Suppose in a given month, $x_{1}$ units of $A$ and $x_{2}$ units of B are used in power generation. So if one unit of A gives the profit of $\$ 0.2$ and one unit of $B \$ 0.3$, then the objective function can be formulated as follows:
Objective function:
Maximize $\quad Z=0.2 x_{1}+0.3 x_{2}$
Subject to the following constraints:
Constraint 1: Cost of fuel
Company had resources of $\$ 7,452$ to spend on fuel for power production. One unit of $\mathrm{A}$, i.e. $100 \mathrm{~kg}$, was purchased at a price of $\$ 1.58$ and $\mathrm{B}$ at $\$ 2.77$. Thus, when $x_{1}$ and $x_{2}$ quantities of fuel $A$ and $B$ types are purchased, it would result in:
$$
1.58 x_{1}+2.77 x_{2} \leq 7,452
$$
Linear Programming: Simplex Method
69
Constraint 2: Amount of electricity generated
With given resources, a maximum of 1,539 mw of electricity was generated out of which fuel A contributed $48 \%$ and B $41 \%$. Thus,
$$
0.48 x_{1}+0.41 x_{2} \leq 1539
$$
Constraint 3: Amount of fuel
A maximum of $440,000 \mathrm{~kg}$ of combined fuel A and B was required to generate this electricity. Out of this total fuel quantity, $160 \mathrm{~kg}$ of fuel A and $120 \mathrm{~kg}$ of B generated a unit of electricity. Thus,
$$
1.6 \mathrm{x}{1}+1.2 \mathrm{x}{2} \leq 4,400
$$
Constraint 4: The number of units of fuels $A$ and $B$
$$
\mathrm{x}{1,} \mathrm{x}{2} \geq 0
$$
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|Case: Adidas AG Retail Stores
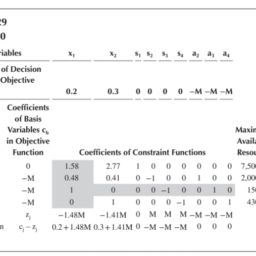
Here the model would be solved by using the simplex method. The model has been reproduced below:
Simplex Method
Maximize Profit $\mathrm{Z}=80 \mathrm{x}{1}+40 \mathrm{x}{2}$
Constraint 1: Accessibility:
$$
9 x_{1}+4 x_{2} \leq 14
$$
Constraint 2: Population density:
$$
2 x_{1}+7 x_{2} \leq 10
$$
Constraint 3: Median Income:
$$
\begin{aligned}
5 \mathrm{x}{1}+10 \mathrm{x}{2} & \leq 20 \
\mathrm{x}{1}, \mathrm{x}{2}, \mathrm{x}_{3} & \geq 0
\end{aligned}
$$

运筹学代考
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|WOODLAND BIOMASS POWER你s
单纯形法需要以下步骤来解决线性规划问题一世磷磷.
步骤 1:模型构建
该案例清楚地说明了燃料 A 和 B 的数量是决定公司利润的变量。假设在给定月份,X1单位一种和X2B 的单位用于发电。因此,如果一单位 A 的利润为$0.2和一个单位乙$0.3,则目标函数可以表述如下:
目标函数:
最大化和=0.2X1+0.3X2
受限于以下约束:约束 1:燃料
成本
$7,452用于发电的燃料。一个单位一种, IE100 到G, 购买价格为$1.58和乙在$2.77. 因此,当X1和X2燃料量一种和乙类型被购买,它会导致:
1.58X1+2.77X2≤7,452
线性规划:单纯形法
69
约束 2:发电量
在给定资源的情况下,燃料 A 贡献的最大发电量为 1,539 兆瓦48%和乙41%. 因此,
0.48X1+0.41X2≤1539
限制 3:燃料量
最多440,000 到G需要混合燃料 A 和 B 来产生这种电力。在这个总燃料量中,160 到G燃料 A 和120 到GB 产生一单位电力。因此,
$$
1.6 \mathrm{x} {1}+1.2 \mathrm{x} {2} \leq 4,400
C○ns吨r一种一世n吨4:吨H和n你米b和r○F你n一世吨s○FF你和一世s$一种$一种nd$乙$
\mathrm{x} {1,} \mathrm{x} {2} \geq 0
$$
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|CASE: ADIDAS AG RETAIL STORES
在这里,模型将使用单纯形法求解。该模型已复制如下:
单纯形法
最大化利润
\begin{aligned}
5 \mathrm{x} {1}+10 \mathrm{x} {2} & \leq 20 \
\mathrm{x} {1}, \mathrm{x} {2}, \mathrm {x}_{3} & \geq 0
\end{对齐}
$$