如果你也在 怎样代写运筹学Operations Research这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。假设检验Hypothesis是假设检验是统计学中的一种行为,分析者据此检验有关人口参数的假设。分析师采用的方法取决于所用数据的性质和分析的原因。假设检验是通过使用样本数据来评估假设的合理性。
运筹学(Operation)是近代应用数学的一个分支。它把具体的问题进行数学抽象,然后用像是统计学、数学模型和算法等方法加以解决,以此来寻找复杂问题中的最佳或近似最佳的解答。
二战中运筹学的应用
在二战时期,作战研究被定义为 “一种科学方法,为执行部门提供有关其控制的行动的决策的量化依据”。它的其他名称包括作战分析(英国国防部从1962年开始)和定量管理。
在第二次世界大战期间,英国有近1000名男女从事作战研究。大约有200名作战研究科学家为英国军队工作。
帕特里克-布莱克特在战争期间为几个不同的组织工作。战争初期,在为皇家飞机研究所(RAE)工作时,他建立了一个被称为 “马戏团 “的团队,帮助减少了击落一架敌机所需的防空炮弹数量,从不列颠战役开始时的平均超过20,000发减少到1941年的4,000发。
my-assignmentexpert™ 运筹学Operations Research作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的运筹学Operations Research作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此运筹学Operations Research作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在运筹学Operations Research作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的应用数学applied math代写服务。我们的专家在运筹学Operations Research代写方面经验极为丰富,各种运筹学Operations Research相关的作业也就用不着 说。
我们提供的假设检验Hypothesis及其相关学科的代写,服务范围广, 其中包括但不限于:
- 商业分析 Business Analysis
- 计算机科学 Computer Science
- 数据挖掘/数据科学/大数据 Data Mining / Data Science / Big Data
- 决策分析 Decision Analytics
- 金融工程 Financial Engineering
- 数据预测 Data Forecasting
- 博弈论 Game Theory
- 地理/地理信息科学 Geography/Geographic Information Science
- 图论 Graph Theory
- 工业工程 Industrial Engineering
- 库存控制 Inventory control
- 数学建模 Mathematical Modeling
- 数学优化 Mathematical Optimization
- 概率和统计 Probability and statistics
- 排队论 Queueing theory
- 社交网络/交通预测模型 Social network/traffic prediction modeling
- 随机过程 Stochastic processes
- 供应链管理 Supply chain management

运筹学代写
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|ILLUSTRATION OF MAXIMIZATION PROBLEM WITH GREATER THAN EQUAL TO CONSTRAINTS
To illustrate the procedure of greater than equal to constraint by introducing surplus variables, the case in $3.1$ is modified by including the following constraints.
Constraint 1 regarding the cost of fuel has marginally increased to $\$ 7,500$. Thus,
$$
1.58 x_{1}+2.77 x_{2} \leq 7,500
$$
Constraint 2 restricted the maximum amount of power to be generated to 1,539 units whereas now if there is limitation in terms of minimum amount of
power, i.e. due to the increased demand, the plant has to produce a minimum of 2,000 units of electricity with one $\mathrm{kg}$ of fuel A producing $0.48$ units and $1 \mathrm{~kg}$ of B producing $0.41$ units. Thus, constraint 2 would be
$$
0.48 x_{1}+0.41 x_{2} \geq 2,000
$$
Finally, constraint 3 in previous case restricted availability of fuel to 4,400 units but with increased demand for power, the amount of fuel required also increases. So, plant tends to keep stock of both types of fuel. If we add two more constraints regarding the opening stock of fuel A and fuel $B$, i.e. opening stock of fuel A is $150 \mathrm{~kg}$ and that of fuel B is $430 \mathrm{~kg}$. Thus,
Constraint $31 \cdot \mathrm{x}{1}+0 \cdot \mathrm{x}{2} \geq 150$
Constraint $40 . \mathrm{x}{1}+1 . \mathrm{x}{2} \geq 430$
Objective function
Maximize $\mathrm{Z}=0.2 \mathrm{x}{1}+0.3 \mathrm{x}{2}$
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|Simplex Method
Step 1: Model Construction
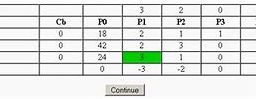
In this case, constraint 1 includes one slack variable, and constraints 2,3 and 4 include three surplus and artificial variables. It is important to notice here that in the case of maximization, coefficients of artificial variables, i.e. $M$ are subtracted from the objective function. Thus, model becomes (Table $3.28$ ).
Step 2: Finding IBFS
The model shown in Table $3.28$ indicates four equations are formed to find values of nine variables; two decision, one slack, three surplus and three artificial variables. To find the initial solution, decision variables $x_{1}$ and $x_{2}, s_{2}, s_{3}$ and $s_{4}$ are put to zero. This would give us the following:
Step 3: Improvement in solution
Iteration 0 :
At this stage, the objective function is zero.
For improvement of solution column that contributes maximum to objective function of maximization would be selected (Table 3.29). Supposing M to be 100 , i.e. an assumed high value:
c –1 1 z = 0.2 + 1.48M = 0.2 + 1.48100 = 148.2 and; c – 2 2 z = 0.3 + 1.41M = 0.3 + 1.41100 = 141.3

运筹学代考
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|ILLUSTRATION OF MAXIMIZATION PROBLEM WITH GREATER THAN EQUAL TO CONSTRAINTS
为了通过引入剩余变量来说明大于等于约束的过程,案例在3.1通过包含以下约束进行修改。
关于燃料成本的约束 1 略微增加到$7,500. 因此,
1.58X1+2.77X2≤7,500
约束 2 将最大发电量限制为 1,539 个单位,而现在如果在最小发电量方面存在限制
电力,即由于需求增加,工厂必须生产至少 2,000 单位的电力,其中一个到G生产燃料 A0.48单位和1 到GB生产的0.41单位。因此,约束 2 将是
0.48X1+0.41X2≥2,000
最后,在前一种情况下,约束 3 将燃料的可用性限制为 4,400 单位,但随着对电力的需求增加,所需的燃料量也会增加。因此,工厂倾向于保留这两种燃料的库存。如果我们再添加两个关于燃料 A 和燃料的期初库存的约束乙,即燃料 A 的期初库存为150 到G燃料 B 是430 到G. 因此,
Constraint 3 1.x1 2 + 0.x ≥ 150
Constraint 4 0.x1 2 + 1.x ≥ 430
数学代写|运筹学作业代写OPERATIONS RESEARCH代考|SIMPLEX METHOD
步骤 1:模型构建
在这种情况下,约束 1 包括一个松弛变量,约束 2,3 和 4 包括三个剩余变量和人工变量。这里需要注意的是,在最大化的情况下,人工变量的系数,即米从目标函数中减去。因此,模型变为吨一种b一世和$3.28$.
第二步:寻找IBFS
模型如表所示3.28表示形成四个方程以求出九个变量的值;两个决策,一个松弛,三个盈余和三个人为变量。为了找到初始解决方案,决策变量X1和X2,s2,s3和s4被置为零。这将为我们提供以下信息:
第 3 步:解决方案的改进
迭代 0:
在此阶段,目标函数为零。
为了改进对最大化目标函数贡献最大的解决方案列吨一种b一世和3.29. 假设 M 为 100 ,即假设的高值:
c –1 1 z = 0.2 + 1.48M = 0.2 + 1.48100 = 148.2 and; c – 2 2 z = 0.3 + 1.41M = 0.3 + 1.41100 = 141.3