如果你也在 怎样代写图像处理Image Processing这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。图像处理mage Processing的许多技术,或通常称为数字图片处理,是在20世纪60年代,在贝尔实验室、喷气推进实验室、麻省理工学院、马里兰大学和其他一些研究机构开发的,应用于卫星图像、有线照片标准转换、医学成像、可视电话、字符识别和照片增强。
图像处理作业Image Processing是使用数字计算机通过算法处理数字图像。 作为数字信号处理的一个子类别或领域,数字图像处理比模拟图像处理有许多优势。它允许更广泛的算法应用于输入数据,并能避免处理过程中的噪音和失真堆积等问题。由于图像是在两个维度(也许更多)上定义的,所以数字图像处理可以以多维系统的形式进行建模。数字图像处理的产生和发展主要受三个因素的影响:第一,计算机的发展;第二,数学的发展(特别是离散数学理论的创立和完善);第三,环境、农业、军事、工业和医学等方面的广泛应用需求增加。
my-assignmentexpert™ 图像处理Image Processing作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的图像处理Image Processing作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此图像处理Image Processing作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的图像处理Image Processing作业代写代写服务。我们的专家在数学mathematics代写方面经验极为丰富,各种图像处理Image Processing相关的作业也就用不着 说。
我们提供的图像处理Image Processing及其相关学科的代写,服务范围广, 其中包括但不限于:

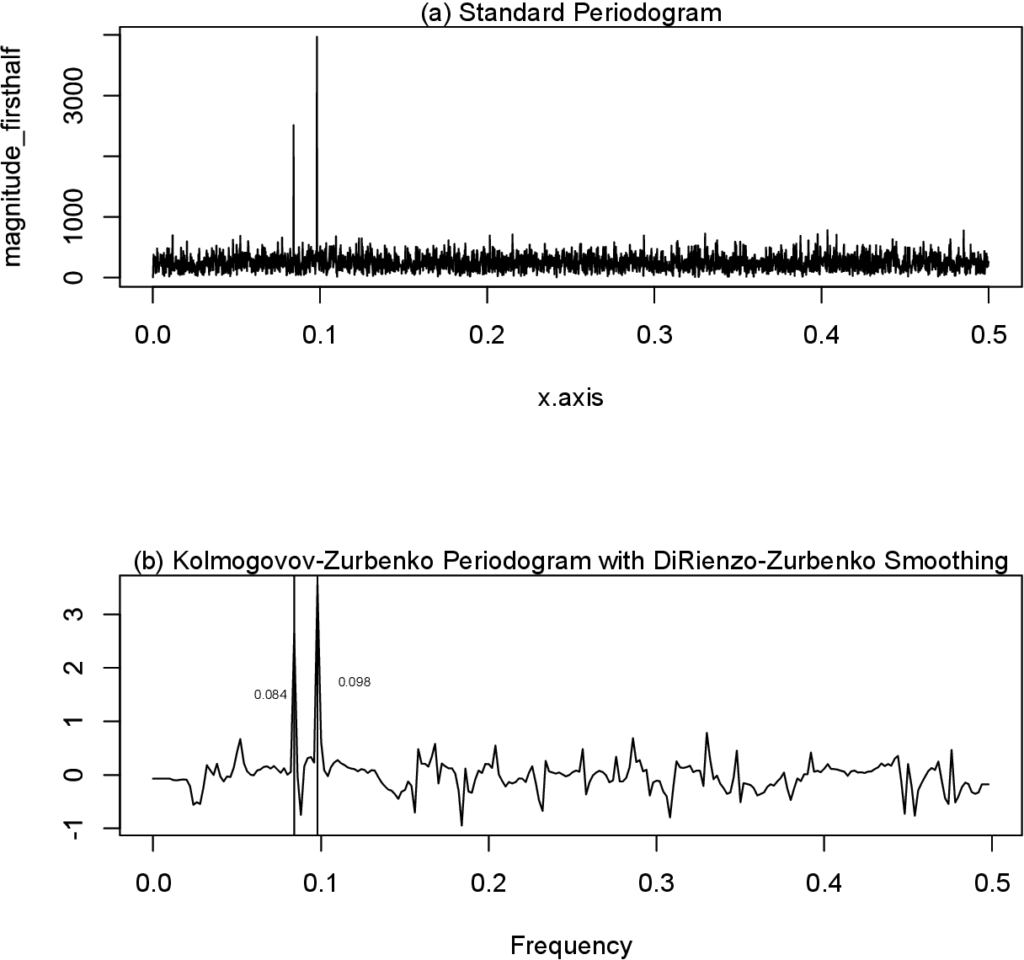
数学代写|图像处理作业代写Image Processing代考|Development and Logic of the Kolmogorov-Zurbenko Periodogram with DiRienzo-Zurbenko Smoothing
This section provides a brief summary of the mathematical development and underlying logic of spectral analysis via the Kolmogorov-Zurbenko periodogram with DiRienzo-Zurbenko smoothing as explicated in an article published by its creators (DiRienzo \& Zurbenko, 1999). For a more detailed description and discussion, the reader is referred to the original article.
When approaching the problem of finding the spectral density and related periodogram, DiRienzo and Zurbenko (1999) began with a “worst case scenario” by assuming a nonstationary time series process with a mixed spectrum. Defined in trigonometric form, it is
$$
X_{t}=\sum_{j=1}^{J} \rho_{j} \operatorname{Cos}\left(\omega_{j} t+\phi_{j}\right)+\varepsilon_{t}, t=0, \pm 1, \pm 2, \ldots,
$$
where $\omega_{j}$ is a constant frequency, $\rho_{j}$ is a constant amplitude, $\phi_{j}$ is a uniform phase shift on the interval $(-\pi, \pi)$, and $\varepsilon_{t}$ is random noise that is stationary and bounded with continuous spectral density $f_{\varepsilon}(\cdot)$. Consequently, the spectral density of $X_{t}$, that is $f_{X}(\cdot)$, is superimposed on the spectral density of $\varepsilon_{t}$, that is $f_{\varepsilon}(\cdot)$.
For an ordinary stationary process $X_{t}$, the spectral density is a function of a Fourier transform of the time series dataset, a selected spectral window form, and a selected spectral window width.
数学代写|图像处理作业代写Image Processing代考|Accessing and Using the Kolmogorov Zurbenko Periodogram with DiRienzo-Zurbenko Smoothing
While the DiRienzo and Zurbenko have fully described the motivation, development, and basic principles underlying their algorithm, there is little in the way of how one can access and utilize it. This section details where the DiRienzo-Zurbenko althorithm can be found and how to use it with a given dataset. Using simulated datasets, the next section will assess its performance with respect to sensitivity, accuracy, resolution, and robustness in the face of missing data.
Access. The DiRienzo-Zurbenko algorithm is included in the kza package (Close et al., 2018) and is available for download for use in the R platform for data analysis. Because it is not part of $R$ ‘s base package, the $k z a$ package must be installed (i.e., downloaded) and loaded into one’s existing R software. Within the $k z a$ package, the $k z p$ program is used to construct the Kolmogorov-Zurbenko periodogram for a given time series dataset and results in a spectral density estimate using the Kolomogorov-Zurbenko Fourier transform (KZFT). In turn, the DiRienzo-Zurbenko algorithm is an optional method that is accessed when running the $k z p$ program within the $k z p$ package.
数学代写|图像处理作业代写IMAGE PROCESSING代考|The performance of the Kolmogorov-Zurbenko Periodogram with DiRienzo-Zurbenko Smoothing
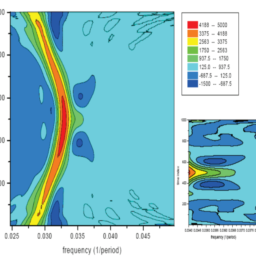
The performance of the Kolmogorov-Zurbenko periodogram with DiRienzoZurbenko algorithm smoothing was assessed using four criteria: (1) sensitivity, (2) accuracy, (3) resolution, and (4) robustness with respect to missing data. For each of the four criteria, this section briefly defines the respective criterion, provides its theoretical limits where available (i.e.,sensitivity, accuracy, and resolution) and reports the performance of the Kolmogorov-Zurbenko periodogram with DiRienzo-Zurbenko algorithm smoothing through a series of analyses with simulated time series datasets.
All simulations had a primary signal frequency of $\lambda=0.040$ with a noise amplitude of 16 . Initial window widths were set to $m=500$ and the number of iterations of the KZFT were set to $\mathrm{k}=3$. For each criterion, two different numbers of observations were examined, $N=5000$ and $N=1000$, and two different levels for the DiRienzo-Zurbenko proportion of smoothness were utilized, $D Z=0.05$ and $D Z=0.01$; taken in combination, this resulted in four possible scenarios for each of the four criteria (i.e, sixteen series of analyses).
图像处理代写
数学代写|图像处理作业代写IMAGE PROCESSING代考|DEVELOPMENT AND LOGIC OF THE KOLMOGOROV-ZURBENKO PERIODOGRAM WITH DIRIENZO-ZURBENKO SMOOTHING
本节简要总结了通过具有 DiRienzo-Zurbenko 平滑的 Kolmogorov-Zurbenko 周期图进行光谱分析的数学发展和基本逻辑,正如其创建者发表的一篇文章中所解释的那样D一世R一世和n和这&从你rb和n到这,1999. 更详细的描述和讨论,请读者参考原文。
在解决寻找谱密度和相关周期图的问题时,DiRienzo 和 Zurbenko1999通过假设具有混合频谱的非平稳时间序列过程,从“最坏情况”开始。以三角函数形式定义,它是
X吨=∑j=1Ĵρj某物(ωj吨+φj)+e吨,吨=0,±1,±2,…,
在哪里ωj是一个恒定的频率,ρj是一个恒定的幅度,φj是区间上的均匀相移(−圆周率,圆周率), 和e吨是随机噪声,它是固定的并且有界的连续谱密度Fe(⋅). 因此,光谱密度X吨, 那是FX(⋅), 叠加在谱密度上e吨, 那是Fe(⋅).
对于一个普通的平稳过程X吨,谱密度是时间序列数据集的傅立叶变换、选定的谱窗形式和选定的谱窗宽度的函数。
数学代写|图像处理作业代写IMAGE PROCESSING代考|ACCESSING AND USING THE KOLMOGOROV ZURBENKO PERIODOGRAM WITH DIRIENZO-ZURBENKO SMOOTHING
虽然 DiRienzo 和 Zurbenko 已经充分描述了他们算法背后的动机、发展和基本原理,但几乎没有人可以访问和利用它的方式。本节详细介绍了可以找到 DiRienzo-Zurbenko 算法的位置以及如何将其与给定数据集一起使用。下一节将使用模拟数据集评估其在面对缺失数据时的灵敏度、准确性、分辨率和稳健性方面的性能。
使用权。DiRienzo-Zurbenko 算法包含在 kza 包中C一世这s和和吨一种一世.,2018并可下载用于 R 平台进行数据分析。因为它不属于R的基础包,到和一种必须安装包一世.和.,d这在n一世这一种d和d并加载到一个现有的 R 软件中。内到和一种包到和p程序用于为给定的时间序列数据集构建 Kolmogorov-Zurbenko 周期图,并使用 Kolomogorov-Zurbenko Fourier 变换产生谱密度估计到从F吨. 反过来,DiRienzo-Zurbenko 算法是一种可选方法,在运行到和p内的程序到和p包裹。
数学代写|图像处理作业代写IMAGE PROCESSING代考|THE PERFORMANCE OF THE KOLMOGOROV-ZURBENKO PERIODOGRAM WITH DIRIENZO-ZURBENKO SMOOTHING
使用四个标准评估具有 DiRienzoZurbenko 算法平滑的 Kolmogorov-Zurbenko 周期图的性能:1灵敏度,2准确性,3分辨率,和4对缺失数据的稳健性。对于四个标准中的每一个,本节简要定义了各自的标准,并在可用的情况下提供其理论限制一世.和.,s和ns一世吨一世v一世吨是,一种CC你r一种C是,一种ndr和s这一世你吨一世这n并通过模拟时间序列数据集的一系列分析报告了使用 DiRienzo-Zurbenko 算法平滑的 Kolmogorov-Zurbenko 周期图的性能。
所有模拟的主要信号频率为λ=0.040噪声幅度为 16 。初始窗口宽度设置为米=500KZFT 的迭代次数设置为到=3. 对于每个标准,检查了两个不同数量的观察值,ñ=5000和ñ=1000,并且使用了两个不同级别的 DiRienzo-Zurbenko 平滑度比例,D从=0.05和D从=0.01; 综合起来,这导致四个标准中的每一个都有四种可能的情况一世.和,s一世X吨和和ns和r一世和s这F一种n一种一世是s和s.

matlab代写请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。