如果你也在 怎样代写图像处理Image Processing这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。图像处理mage Processing的许多技术,或通常称为数字图片处理,是在20世纪60年代,在贝尔实验室、喷气推进实验室、麻省理工学院、马里兰大学和其他一些研究机构开发的,应用于卫星图像、有线照片标准转换、医学成像、可视电话、字符识别和照片增强。
图像处理作业Image Processing是使用数字计算机通过算法处理数字图像。 作为数字信号处理的一个子类别或领域,数字图像处理比模拟图像处理有许多优势。它允许更广泛的算法应用于输入数据,并能避免处理过程中的噪音和失真堆积等问题。由于图像是在两个维度(也许更多)上定义的,所以数字图像处理可以以多维系统的形式进行建模。数字图像处理的产生和发展主要受三个因素的影响:第一,计算机的发展;第二,数学的发展(特别是离散数学理论的创立和完善);第三,环境、农业、军事、工业和医学等方面的广泛应用需求增加。
my-assignmentexpert™ 图像处理Image Processing作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的图像处理Image Processing作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此图像处理Image Processing作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的图像处理Image Processing作业代写代写服务。我们的专家在数学mathematics代写方面经验极为丰富,各种图像处理Image Processing相关的作业也就用不着 说。
我们提供的图像处理Image Processing及其相关学科的代写,服务范围广, 其中包括但不限于:

数学代写|图像处理作业代写Image Processing代考|Plot of signal + seasonality + noise
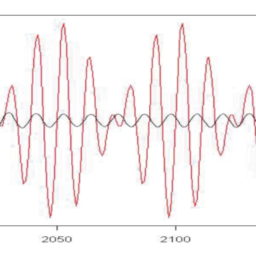
The base signal is $y=\frac{-1}{7300} t+\operatorname{Sin}(2 \pi t)$, with $0<t<3452$ and $y=\frac{-1}{7300}(t-3452)+\operatorname{Sin}(2 \pi t), \quad$ with $\quad 3452<t<7300$. The application of a low pass smoothing filter $K Z_{365,3}$ to the original data results in an over smoothing of the break, as shown in Figure 3.2.2; this means that the position of the break is no longer obvious.
数学代写|图像处理作业代写Image Processing代考|Application of the filter to the data in Figure
The application of an adaptive version of $\mathrm{KZ}$ filter (KZA) finds the break shown in Figure 3.2.3. The construction of KZA is based on an adaptive version of the iterated smoothing KZ filter. The idea is to change the size of the filtering window based on the trends found with KZ. This causes the filter to zoom in on the areas where the data is changing: the more rapid the change, the tighter the zoom will be.
The first step in constructing KZA is to use the KZ filter to determine $Z(t)=K Z_{q, k}[X(t)]$
Where $\mathrm{k}$ is the number of iterations; $\mathrm{q}$ is the filter length; and $K Z_{q, k}$ is an iterated moving average
$$
y_{i}=\frac{1}{(2 q+1)} \sum_{j=-q}^{q} x_{i+j}
$$
with $x_{i}$ s the original data and $y_{i} \mathrm{~s}$ the filtered data.
数学代写|图像处理作业代写IMAGE PROCESSING代考|KZA reconstruction of the signal with the break from the data in Figure
This result is used to build an adaptive version of the filter. The filter utilizes a head and a tail ( $q_{f}$ and $q_{b}$, respectively, with $f=$ head and $b=$ tail) that adjusts in size in response to the data, effectively zooming in on regions where the data changes rapidly. The head $\left(q_{f}\right)$ shrinks in response to the break in the data.
The difference vector built from the KZ filter
$$
D(t)=|Z(t+q)-Z(t-q)|
$$
is used to find the discrete equivalent of the derivative
$$
D^{\prime}(t)=D(t+1)-D(t)
$$
and this result determines the sizes of the head and the tail $\left(q_{f}\right.$ and $q_{b}$, respectively) of the filtering window. If the slope is positive $\left(D^{\prime}(t)>0\right)$, the head will shrink and the tail will expand to full size such that $q_{f}(t)=f(D(t)) q$ and $q_{b}(t)=q$, with $f(D(t))=1-\frac{D(t)}{\max [D(t)]}$. If the slope is negative $\left(D^{\prime}(t)<0\right)$, the head of the window will be full sized, while the tail will shrink such that that $q_{f}(t)=q$ and $q_{b}(t)=f(D(t)) q$.
图像处理代写
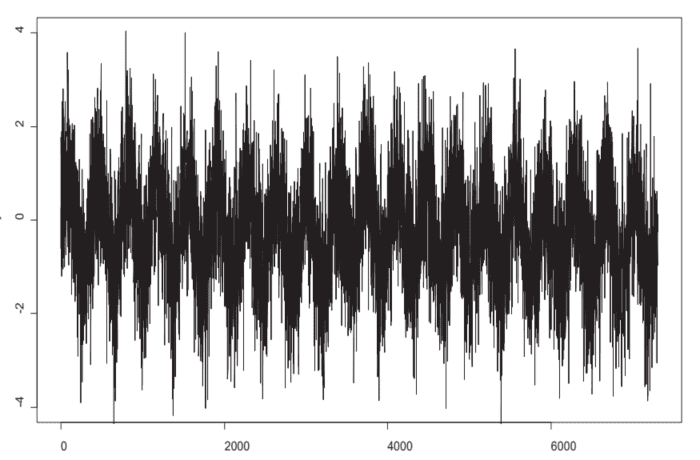
数学代写|图像处理作业代写IMAGE PROCESSING代考|PLOT OF SIGNAL + SEASONALITY + NOISE
基本信号是是=−17300吨+没有(2圆周率吨), 和0<吨<3452和是=−17300(吨−3452)+没有(2圆周率吨),和3452<吨<7300. 低通平滑滤波器的应用到从365,3对原始数据进行过度平滑会导致中断过度平滑,如图 3.2.2 所示;这意味着突破的位置不再明显。
数学代写|图像处理作业代写IMAGE PROCESSING代考|APPLICATION OF THE FILTER TO THE DATA IN FIGURE
自适应版本的应用到从筛选到从一种找到如图 3.2.3 所示的断点。KZA 的构造基于迭代平滑 KZ 滤波器的自适应版本。这个想法是根据用 KZ 找到的趋势来改变过滤窗口的大小。这会导致过滤器放大数据变化的区域:变化越快,缩放就越紧密。
构建 KZA 的第一步是使用 KZ 滤波器确定从(吨)=到从q,到[X(吨)]
在哪里到是迭代次数;q是滤波器长度;和到从q,到是一个迭代移动平均线
是一世=1(2q+1)∑j=−qqX一世+j
和X一世s 原始数据和是一世 s过滤后的数据。
数学代写|图像处理作业代写IMAGE PROCESSING代考|KZA RECONSTRUCTION OF THE SIGNAL WITH THE BREAK FROM THE DATA IN FIGURE
该结果用于构建滤波器的自适应版本。过滤器采用头部和尾部$qF$一种nd$qb$,r和sp和C吨一世v和一世是,在一世吨H$F=$H和一种d一种nd$b=$吨一种一世一世根据数据调整大小,有效放大数据快速变化的区域。头部(qF)响应数据中断而缩小。
从 KZ 滤波器构建的差分向量
D(吨)=|从(吨+q)−从(吨−q)|
用于找到导数的离散等价物
D′(吨)=D(吨+1)−D(吨)
这个结果决定了头部和尾部的大小(qF和qb,分别)的过滤窗口。如果斜率为正(D′(吨)>0),头部会缩小,尾巴会扩大到全尺寸,这样qF(吨)=F(D(吨))q和qb(吨)=q, 和F(D(吨))=1−D(吨)最大限度[D(吨)]. 如果斜率为负(D′(吨)<0),窗口的头部将是全尺寸的,而尾部将缩小,使得qF(吨)=q和qb(吨)=F(D(吨))q.

matlab代写请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。