如果你也在 怎样代写图像处理Image Processing这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。图像处理mage Processing的许多技术,或通常称为数字图片处理,是在20世纪60年代,在贝尔实验室、喷气推进实验室、麻省理工学院、马里兰大学和其他一些研究机构开发的,应用于卫星图像、有线照片标准转换、医学成像、可视电话、字符识别和照片增强。
图像处理作业Image Processing是使用数字计算机通过算法处理数字图像。 作为数字信号处理的一个子类别或领域,数字图像处理比模拟图像处理有许多优势。它允许更广泛的算法应用于输入数据,并能避免处理过程中的噪音和失真堆积等问题。由于图像是在两个维度(也许更多)上定义的,所以数字图像处理可以以多维系统的形式进行建模。数字图像处理的产生和发展主要受三个因素的影响:第一,计算机的发展;第二,数学的发展(特别是离散数学理论的创立和完善);第三,环境、农业、军事、工业和医学等方面的广泛应用需求增加。
my-assignmentexpert™ 图像处理Image Processing作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的图像处理Image Processing作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此图像处理Image Processing作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的图像处理Image Processing作业代写代写服务。我们的专家在数学mathematics代写方面经验极为丰富,各种图像处理Image Processing相关的作业也就用不着 说。
我们提供的图像处理Image Processing及其相关学科的代写,服务范围广, 其中包括但不限于:
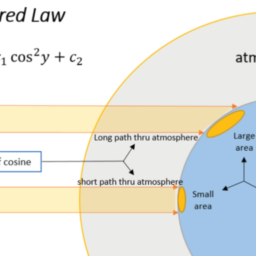
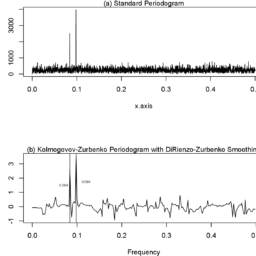
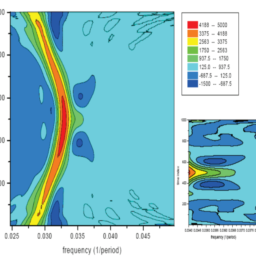
数学代写|图像处理作业代写Image Processing代考|Reconstruction of a sine wave with period of 12.5 units time using KZFT.
Due to the positive results of the reconstruction a periodic signal embedded in noise, the complexity of the signal and simulations were augmented to review the KZFT filter’s reconstructive capability for a periodic signal that was the summation of two sine waves plus noise, $Y_{3}=\sin (2 \pi(0.08) t)+$ $\sin (2 \pi(0.10) t)+N(0,1)$. In order to reconstruct this signal, the standard method was first considered. This method involves applying a band-pass filter with a center that is the midpoint of the two frequencies of interest.
数学代写|图像处理作业代写Image Processing代考|Band-pass filter application with center at the midpoint of two frequencies reveals very poor recovery of the original signal.
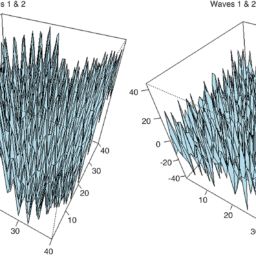
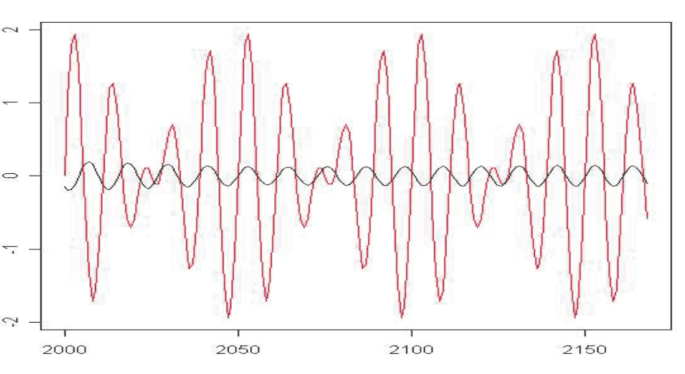
Since the standard method proved to be unsuccessful at recovering the true periodic signal, a new method was used. This new method to reconstruct the periodic signal involved taking the sum of two KZFT filters, which were the approximate dominant frequencies. In order to utilize this method, the number of iterations (parameter $k$ ) must be chosen at a high enough level in order to avoid energy leakage from the second peak in the transfer function. This method was used to reconstruct the signal, $Y_{3}=\sin (2 \pi(0.08) t)+$ $\sin (2 \pi(0.10) t)+N(0,1)$. It was also used to reconstruct this signal when the noise levels were increased up to a variance of 64 ; this had a high level of success, as the R-squared values were at least $98.2 \%$. The signal, $Y_{4}=$ $\sin (2 \pi(0.08) t)+\sin (2 \pi(0.10) t)+N(0,64)$ is displayed in Figure 7.1.3 and is plotted against the true periodic signal (without noise). Figure 7.1.4 displays the reconstruction of the periodic signal using the sum of two KZFT filters.
数学代写|图像处理作业代写IMAGE PROCESSING代考|Application: The KZFT reconstruction of the sum of two sine waves with frequencies 0.08 and 0.10 cycles per unit time plus noise~N(0,64).
This method of applying the KZFT filter to the dominant frequencies in the data determined from the spectrum proved to be successful. Therefore, the complexity of the signal was increased to the sum of four sine waves plus noise. Consider the signal, $Y_{5}=\sin (2 \pi(0.04) t)+\sin (2 \pi(0.05) t)+$ $\sin (2 \pi(0.08) t)+\sin (2 \pi(0.10) t)+N(0,16)$, as shown in Figure $7.1 .5$ along with the true periodic signal. The sum of four KZFT filters was used to reconstruct the periodic signal, which proved to be very successful and is displayed in Figure 7.1.6. The R-squared values for this signal recovery ranged from $96-99.4 \%$ as the window size increased.

图像处理代写
数学代写|图像处理作业代写IMAGE PROCESSING代考|RECONSTRUCTION OF A SINE WAVE WITH PERIOD OF 12.5 UNITS TIME USING KZFT.
由于重建嵌入噪声中的周期信号的积极结果,信号和模拟的复杂性被增强,以审查 KZFT 滤波器对周期信号的重建能力,该周期信号是两个正弦波加噪声的总和,是3=没有(2圆周率(0.08)吨)+ 没有(2圆周率(0.10)吨)+ñ(0,1). 为了重建这个信号,首先考虑了标准方法。该方法涉及应用带通滤波器,其中心是两个感兴趣频率的中点。
数学代写|图像处理作业代写IMAGE PROCESSING代考|BAND-PASS FILTER APPLICATION WITH CENTER AT THE MIDPOINT OF TWO FREQUENCIES REVEALS VERY POOR RECOVERY OF THE ORIGINAL SIGNAL.
由于标准方法被证明无法成功恢复真实的周期性信号,因此使用了一种新方法。这种重建周期信号的新方法涉及采用两个 KZFT 滤波器的总和,它们是近似的主频率。为了利用这种方法,迭代次数p一种r一种米和吨和r$到$必须选择足够高的电平以避免能量从传递函数中的第二个峰值泄漏。该方法用于重构信号,是3=没有(2圆周率(0.08)吨)+ 没有(2圆周率(0.10)吨)+ñ(0,1). 当噪声水平增加到方差为 64 时,它也被用来重建这个信号;这取得了很高的成功,因为 R 平方值至少是98.2%. 信号,是4= 没有(2圆周率(0.08)吨)+没有(2圆周率(0.10)吨)+ñ(0,64)显示在图 7.1.3 中,并针对真实的周期信号绘制在一世吨H这你吨n这一世s和. 图 7.1.4 显示了使用两个 KZFT 滤波器之和对周期信号的重构。
数学代写|图像处理作业代写IMAGE PROCESSING代考|APPLICATION: THE KZFT RECONSTRUCTION OF THE SUM OF TWO SINE WAVES WITH FREQUENCIES 0.08 AND 0.10 CYCLES PER UNIT TIME PLUS NOISE~N0,64.
这种将 KZFT 滤波器应用于从频谱确定的数据中的主要频率的方法被证明是成功的。因此,信号的复杂性增加到四个正弦波加上噪声的总和。考虑信号,是5=没有(2圆周率(0.04)吨)+没有(2圆周率(0.05)吨)+ 没有(2圆周率(0.08)吨)+没有(2圆周率(0.10)吨)+ñ(0,16),如图7.1.5以及真实的周期信号。四个 KZFT 滤波器的总和用于重构周期信号,证明非常成功,如图 7.1.6 所示。此信号恢复的 R 平方值范围为96−99.4%随着窗口大小的增加。

matlab代写请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。