如果你也在 怎样代写理论力学Theoretical Mechanics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。理论力学Theoretical Mechanics是一组密切相关的经典力学的替代公式。它是由许多科学家和数学家在18世纪及以后,在牛顿力学之后发展起来的。由于牛顿力学考虑的是运动的矢量,特别是系统中各组成部分的加速度、动量、力,因此由牛顿定律和欧拉定律所支配的力学的另一个名称是矢量力学。
理论力学Theoretical Mechanics使用代表系统整体的运动标量属性–通常是其总动能和势能–而不是牛顿对单个粒子的矢量力。运动方程是由标量通过一些关于标量变化的基本原理推导出来的。分析力学使用代表系统整体的运动标量属性–通常是其总动能和势能–而不是牛顿对单个粒子的矢量力。运动方程是由标量通过一些关于标量变化的基本原理推导出来的。
my-assignmentexpert™ 理论力学Theoretical Mechanics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的理论力学Theoretical Mechanics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此理论力学Theoretical Mechanics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在物理physics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的理论力学Theoretical Mechanics代写服务。我们的专家在物理physics代写方面经验极为丰富,各种理论力学Theoretical Mechanics相关的作业也就用不着 说。
我们提供的理论力学Theoretical Mechanics及其相关学科的代写,服务范围广, 其中包括但不限于:
物理代写|理论力学作业代写Theoretical Mechanics代考|Homogeneity of Time
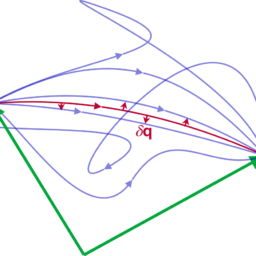
We call a system ‘temporally homogeneous’ if its properties prove to be invariant under time translations. The results of measurements performed under exactly the same boundary conditions are independent of the point in time of the measurement. The ensemble of all possible paths which start at a certain given time is independent of the choice of this initial time but only dependent on the initial configuration $\mathbf{q}{a}$. If $\mathbf{q}(t)$ is the configuration path which the system is passing through between the times $t{a}$ and $t_{e}$ with the initial- and end-configurations
$$
\mathbf{q}\left(t_{a}\right)=\mathbf{q}{a} \quad \text { and } \quad \mathbf{q}\left(t{e}\right)=\mathbf{q}{e}, $$ then the ‘temporally shifted’ configuration path between $t{a}+\Delta t$ and $t_{e}+\Delta t$ will go through, provided the temporal homogeneity is given, exactly the same points of the configuration space if only the initial- and end-configurations are the same:
$$
\mathbf{q}\left(t_{a}+\Delta t\right)=\mathbf{q}{a} ; \quad \mathbf{q}\left(t{e}+\Delta t\right)=\mathbf{q}_{e}
$$
This means, however, that the Lagrangian $L$ of the system by which we calculate its path can not explicitly depend on the time:
homogeneity of time $\Longleftrightarrow \frac{\partial L}{\partial t}=0$.
物理代写|理论力学作业代写Theoretical Mechanics代考|Homogeneity of Space
A system is called ‘spatially homogeneous’ if its properties are independent of its position, i.e. if a rigid shift of the system as a whole does not change the results of measurement. That, for instance, is the case when the considered system is subject exclusively to (internal) forces which depend only on the interparticle-distances.
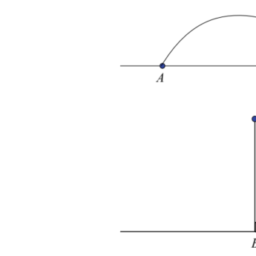
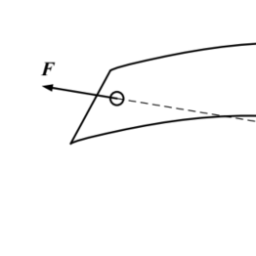
The generalized coordinate $q_{j}$ may be chosen in such a way that $\Delta q_{j}$ means a translation of the total system (Fig. 1.53). That can be realized, e.g., by the Cartesian components of the center of mass. Then it follows as sufficient condition for spatial homogeneity:
$$
\frac{\partial L}{\partial q_{j}}=0
$$
$q_{j}$ is therefore cyclic leading to the conservation law:
$$
p_{j}=\frac{\partial L}{\partial \dot{q}{j}}=\text { const } $$ But what is the physical meaning of $p{j}$ ? Since the system is thought to be conservative it holds:
$$
\frac{\partial V}{\partial \dot{q}{j}}=0 $$ and therewith also: $$ p{j}=\frac{\partial L}{\partial \dot{q}{j}}=\frac{\partial T}{\partial \dot{q}{j}}=\sum_{i=1}^{N} m_{i} \dot{\mathbf{r}}{i} \frac{\partial \dot{\mathbf{r}}{i}}{\partial \dot{q}{j}}=\sum{i=1}^{N} m_{i} \dot{\mathbf{r}}{i} \frac{\partial \mathbf{r}{i}}{\partial q_{j}}
$$
物理代写|理论力学作业代写THEORETICAL MECHANICS代考|Isotropy of Space
One calls a system ‘spatially isotropic’ if the system properties do not change on arbitrary rotations. We now choose the generalized coordinate $q_{j}$ such that $\Delta q_{j}$ represents a rotation of the system by an angle $\Delta \varphi$ around the axial direction $\mathbf{n}{j}$ (see Fig. 1.55): $$ \left|\Delta \mathbf{r}{i}\right|=\Delta q_{j} r_{i} \sin \vartheta_{i}
$$
$\Delta \mathbf{r}{i}$ is orthogonal to $\mathbf{r}{i}$ and to $\mathbf{n}{j}$. It therefore holds: $$ \Delta \mathbf{r}{i}=\Delta q_{j} \mathbf{n}{j} \times \mathbf{r}{i}
$$
It follows as sufficient condition for spatial isotropy:
$$
\frac{\partial L}{\partial q_{j}}=0
$$

理论力学代写
物理代写|理论力学作业代写THEORETICAL MECHANICS代考|HOMOGENEITY OF TIME
如果一个系统的属性在时间转换下被证明是不变的,我们就称它为“时间同质的”系统。在完全相同的边界条件下执行的测量结果与测量时间点无关。从某个给定时间开始的所有可能路径的集合与该初始时间的选择无关,而仅取决于初始配置
$$
\mathbf{q}\left(t_{a}\right)=\mathbf{q}{a} \quad \text { and } \quad \mathbf{q}\left(t{e}\right)=\mathbf{q}{e}, $$ then the ‘temporally shifted’ configuration path between $t{a}+\Delta t$ and $t_{e}+\Delta t$ will go through, provided the temporal homogeneity is given, exactly the same points of the configuration space if only the initial- and end-configurations are the same:
$$
\mathbf{q}\left(t_{a}+\Delta t\right)=\mathbf{q}{a} ; \quad \mathbf{q}\left(t{e}+\Delta t\right)=\mathbf{q}_{e}
$$
然而,这意味着拉格朗日大号我们计算其路径的系统不能明确地依赖于时间:时间的
同质性⟺∂大号∂吨=0.
物理代写|理论力学作业代写THEORETICAL MECHANICS代考|HOMOGENEITY OF SPACE
如果系统的属性与其位置无关,即如果系统作为一个整体的刚性移动不会改变测量结果,则系统被称为“空间均匀的”。例如,当所考虑的系统完全受制于一世n吨和rn一种一世仅取决于粒子间距离的力。
广义坐标qj可以这样选择Δqj表示整个系统的翻译F一世G.1.53. 这可以例如通过质心的笛卡尔分量来实现。那么它作为空间同质性的充分条件:
∂大号∂qj=0
qj因此是循环导致守恒定律:
$$
\frac{\partial L}{\partial q_{j}}=0
$$
$q_{j}$ is therefore cyclic leading to the conservation law:
$$
p_{j}=\frac{\partial L}{\partial \dot{q}{j}}=\text { const } $$ But what is the physical meaning of $p{j}$ ? Since the system is thought to be conservative it holds:
$$
\frac{\partial V}{\partial \dot{q}{j}}=0 $$ and therewith also: $$ p{j}=\frac{\partial L}{\partial \dot{q}{j}}=\frac{\partial T}{\partial \dot{q}{j}}=\sum_{i=1}^{N} m_{i} \dot{\mathbf{r}}{i} \frac{\partial \dot{\mathbf{r}}{i}}{\partial \dot{q}{j}}=\sum{i=1}^{N} m_{i} \dot{\mathbf{r}}{i} \frac{\partial \mathbf{r}{i}}{\partial q_{j}}
$$
物理代写|理论力学作业代写THEORETICAL MECHANICS代考|ISOTROPY OF SPACE
如果系统属性不随任意旋转发生变化,则将系统称为“空间各向同性”。我们现在选择广义坐标qj这样Δqj表示系统旋转一个角度Δ披绕轴向 $\mathbf{n} {j}(s和和F一世G.1.55):$ \left|\Delta \mathbf{r} {i}\right|=\Delta q_{j} r_{i} \sin \vartheta_{i}
$$
$\Delta \mathbf{r}{i}$ is orthogonal to $\mathbf{r}{i}$ and to $\mathbf{n}{j}$. It therefore holds: $$ \Delta \mathbf{r}{i}=\Delta q_{j} \mathbf{n}{j} \times \mathbf{r}{i}
$$
It follows as sufficient condition for spatial isotropy:
$$
\frac{\partial L}{\partial q_{j}}=0
$$

物理代写|理论力学作业代写Theoretical Mechanics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。