如果你也在 怎样代写理论力学Theoretical Mechanics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。理论力学Theoretical Mechanics是一组密切相关的经典力学的替代公式。它是由许多科学家和数学家在18世纪及以后,在牛顿力学之后发展起来的。由于牛顿力学考虑的是运动的矢量,特别是系统中各组成部分的加速度、动量、力,因此由牛顿定律和欧拉定律所支配的力学的另一个名称是矢量力学。
理论力学Theoretical Mechanics使用代表系统整体的运动标量属性–通常是其总动能和势能–而不是牛顿对单个粒子的矢量力。运动方程是由标量通过一些关于标量变化的基本原理推导出来的。分析力学使用代表系统整体的运动标量属性–通常是其总动能和势能–而不是牛顿对单个粒子的矢量力。运动方程是由标量通过一些关于标量变化的基本原理推导出来的。
my-assignmentexpert™ 理论力学Theoretical Mechanics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的理论力学Theoretical Mechanics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此理论力学Theoretical Mechanics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在物理physics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的理论力学Theoretical Mechanics代写服务。我们的专家在物理physics代写方面经验极为丰富,各种理论力学Theoretical Mechanics相关的作业也就用不着 说。
我们提供的理论力学Theoretical Mechanics及其相关学科的代写,服务范围广, 其中包括但不限于:
物理代写|理论力学作业代写Theoretical Mechanics代考|Representation Spaces
We want to discuss in this section some abstract terms which will turn out to be useful for our further considerations. Some of them we have already repeatedly used. We start with a classification of the representation spaces.
(1) Configuration Space
This representation space is already known to us. It has the
dimension: $S$
and as
axes: $\quad \mathbf{q}=\left(q_{1}, q_{2}, \ldots, q_{s}\right)$.
Example: Linear Harmonic Oscillator
(see Example 2 in Sect. 2.2.2)
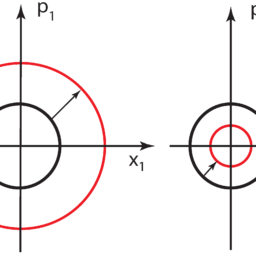
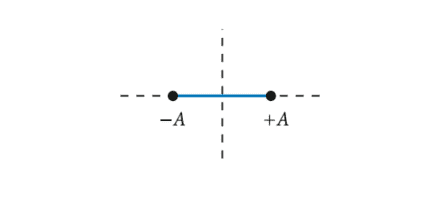
The configuration space is here the $x$-axis. The configuration path is built by all $x$ for which $|x| \leq A$.
By specification of the configuration path the mechanical problem is not yet solved because it remains unclear where the system finds itself at a certain point of time (Fig. 2.9).
(2) Event Space
dimension: $\quad S+1$,
axes: $\quad \mathbf{q}=\left(q_{1}, q_{2}, \ldots, q_{S}\right) \quad$ and $t$.
The path in the event space $(\mathbf{q}, t)$ is definitely calculable if $2 S$ initial conditions are given. These can be the configurations at two different times, $\left(\mathbf{q}\left(t_{1}\right), \mathbf{q}\left(t_{2}\right)\right)$, or $S$ generalized coordinates and the corresponding $S$ generalized velocities at a certain point of time $t_{0},\left(\mathbf{q}\left(t_{0}\right), \dot{\mathbf{q}}\left(t_{0}\right)\right)$ :
Lagrange formalism $\Longleftrightarrow$ event space.
Example: Linear Harmonic Oscillator
Because of $S=1$ two initial conditions are necessary in order to fix uniquely the path in the event space.
物理代写|理论力学作业代写Theoretical Mechanics代考|Fundamental Poisson Brackets
We now want to introduce the concept of the Poisson brackets. This concept allows for an especially concise formulation of the classical equations of motion and the conservation laws. That will be demonstrated in the following.
After the pre-considerations of the last section we know that any arbitrary mechanical observable can be represented as a phase function:
$$
f(\pi, t)=f(\mathbf{q}, \mathbf{p}, t)
$$
Let us investigate its equation of motion:
$$
\begin{aligned}
\frac{d f}{d t} &=\sum_{j=1}^{S}\left(\frac{\partial f}{\partial q_{j}} \dot{q}{j}+\frac{\partial f}{\partial p{j}} \dot{p}{j}\right)+\frac{\partial f}{\partial t} \ &=\sum{j=1}^{S}\left(\frac{\partial f}{\partial q_{j}} \frac{\partial H}{\partial p_{j}}-\frac{\partial f}{\partial p_{j}} \frac{\partial H}{\partial q_{j}}\right)+\frac{\partial f}{\partial t}
\end{aligned}
$$
Definition 2.4.2 $f=f(\mathbf{q}, \mathbf{p}, t), g=g(\mathbf{q}, \mathbf{p}, t)$ : scalar functions of the vector pairs $\mathbf{q}=\left(q_{1}, \ldots, q_{S}\right), \mathbf{p}=\left(p_{1}, \ldots, p_{S}\right)$.
$$
{f, g}_{\mathbf{q}, \mathbf{p}} \equiv \sum_{j=1}^{S}\left(\frac{\partial f}{\partial q_{j}} \frac{\partial g}{\partial p_{j}}-\frac{\partial f}{\partial p_{j}} \frac{\partial g}{\partial q_{j}}\right)
$$
‘Poisson bracket’ of $f$ with $g$.
By the subscripts at the bracket-symbol on the left-hand side it is referred to the variables with respect to which the differentiations have to be performed. However, later we will recognize that this is in principle unnecessary. As an important result it will turn out that the Poisson bracket is independent of the choice of canonical variables by which the differentiations are explicitly done.
物理代写|理论力学作业代写THEORETICAL MECHANICS代考|Formal Properties
Up to now the introduction of the Poisson bracket implied solely a simplification of the scientific notation and does not bring us a step further in the solution of a practical problem. Important are, however, some algebraic properties which allow for a generalization going distinctly beyond the framework of classical mechanics. First we list these properties and bring the proof, where it is not obvious, afterwards: antisymmetry
$$
{f, g}=-{g, f} ; \quad{f, f}=0 \quad \forall f .
$$
linearity
$$
\begin{aligned}
&\left{c_{1} f_{1}+c_{2} f_{2}, g\right}=c_{1}\left{f_{1}, g\right}+c_{2}\left{f_{2}, g\right}, \quad c_{1}, c_{2}: \text { const } \
&\text { zero (null) element } \
&{c, g}=0 \quad \forall g=g(\mathbf{q}, \mathbf{p}), \quad c: \text { constant }
\end{aligned}
$$
product rule
$$
{f, g h}=g{f, h}+{f, g} h
$$
Jacobi identity
$$
{f,{g, h}}+{g,{h, f}}+{h,{f, g}}=0
$$
Equations (2.115)-(2.117) follow directly from the Definition (2.104) of the bracket. The same holds for (2.118), too, when the product rule for differentiations is applied. The proof of Eq. (2.119) follows, even though a bit lengthy, simply by insertion or more elegantly as follows:
At first we express the Poisson bracket by a differential operator,
$$
{g, h}=D_{g} h
$$
where
$$
D_{g}=\sum_{j=1}^{S}\left(\frac{\partial g}{\partial q_{j}} \frac{\partial}{\partial p_{j}}-\frac{\partial g}{\partial p_{j}} \frac{\partial}{\partial q_{j}}\right) \equiv \sum_{i=1}^{2 S} \alpha_{i}(g) \frac{\partial}{\partial \pi_{i}}
$$

理论力学代写
物理代写|理论力学作业代写THEORETICAL MECHANICS代考|REPRESENTATION SPACES
我们想在本节中讨论一些抽象术语,这些术语将对我们的进一步考虑有用。其中一些我们已经反复使用过。我们从表示空间的分类开始。
1配置空间
这个表示空间是我们已经知道的。它具有以下
维度:小号
并作为
轴:q=(q1,q2,…,qs).
示例:线性谐波振荡器
s和和和X一种米p一世和2一世n小号和C吨.2.2.2
配置空间在这里X-轴。配置路径由所有人构建X为此|X|≤一种.
通过配置路径的规范,机械问题尚未解决,因为系统在某个时间点发现自己的位置仍不清楚F一世G.2.9.
2活动空间
维度:小号+1,
轴:q=(q1,q2,…,q小号)和吨.
活动空间中的路径(q,吨)是绝对可以计算的,如果2小号给出了初始条件。这些可以是两个不同时间的配置,(q(吨1),q(吨2)), 或者小号广义坐标和对应的小号某一时间点的广义速度吨0,(q(吨0),q˙(吨0)):
拉格朗日形式主义⟺活动空间。
示例:线性谐波振荡器
因为小号=1为了在事件空间中唯一地确定路径,需要两个初始条件。
物理代写|理论力学作业代写THEORETICAL MECHANICS代考|FUNDAMENTAL POISSON BRACKETS
我们现在要介绍泊松括号的概念。这个概念允许对经典运动方程和守恒定律进行特别简洁的表述。这将在下面演示。
在上一节的预先考虑之后,我们知道任何任意的机械可观测量都可以表示为相位函数:
F(圆周率,吨)=F(q,p,吨)
让我们研究它的运动方程:
$$
f(\pi, t)=f(\mathbf{q}, \mathbf{p}, t)
$$
Let us investigate its equation of motion:
$$
\begin{aligned}
\frac{d f}{d t} &=\sum_{j=1}^{S}\left(\frac{\partial f}{\partial q_{j}} \dot{q}{j}+\frac{\partial f}{\partial p{j}} \dot{p}{j}\right)+\frac{\partial f}{\partial t} \ &=\sum{j=1}^{S}\left(\frac{\partial f}{\partial q_{j}} \frac{\partial H}{\partial p_{j}}-\frac{\partial f}{\partial p_{j}} \frac{\partial H}{\partial q_{j}}\right)+\frac{\partial f}{\partial t}
\end{aligned}
$$
Definition 2.4.2 $f=f(\mathbf{q}, \mathbf{p}, t), g=g(\mathbf{q}, \mathbf{p}, t)$ : scalar functions of the vector pairs $\mathbf{q}=\left(q_{1}, \ldots, q_{S}\right), \mathbf{p}=\left(p_{1}, \ldots, p_{S}\right)$.
$$
{f, g}_{\mathbf{q}, \mathbf{p}} \equiv \sum_{j=1}^{S}\left(\frac{\partial f}{\partial q_{j}} \frac{\partial g}{\partial p_{j}}-\frac{\partial f}{\partial p_{j}} \frac{\partial g}{\partial q_{j}}\right)
$$
‘泊松括号’ ofF和G.
通过左侧括号符号的下标,它指的是必须执行微分的变量。但是,稍后我们将认识到这在原则上是不必要的。作为一个重要的结果,泊松括号独立于规范变量的选择,通过这些变量显式地完成微分。
物理代写|理论力学作业代写THEORETICAL MECHANICS代考|FORMAL PROPERTIES
到目前为止,泊松括号的引入仅仅意味着对科学计数法的简化,并没有使我们在解决实际问题上更进一步。然而,重要的是一些代数性质,这些性质允许进行明显超出经典力学框架的概括。首先,我们列出这些性质并在不明显的地方提供证明,然后:反对称
$$
{f, g}=-{g, f} ; \quad{f, f}=0 \quad \forall f .
$$
linearity
$$
\begin{aligned}
&\left{c_{1} f_{1}+c_{2} f_{2}, g\right}=c_{1}\left{f_{1}, g\right}+c_{2}\left{f_{2}, g\right}, \quad c_{1}, c_{2}: \text { const } \
&\text { zero (null) element } \
&{c, g}=0 \quad \forall g=g(\mathbf{q}, \mathbf{p}), \quad c: \text { constant }
\end{aligned}
$$
product rule
$$
{f, g h}=g{f, h}+{f, g} h
$$
Jacobi identity
$$
{f,{g, h}}+{g,{h, f}}+{h,{f, g}}=0
$$
Equations (2.115)-(2.117) follow directly from the Definition (2.104) of the bracket. The same holds for (2.118), too, when the product rule for differentiations is applied. The proof of Eq. (2.119) follows, even though a bit lengthy, simply by insertion or more elegantly as follows:
At first we express the Poisson bracket by a differential operator,
$$
{g, h}=D_{g} h
$$
where
$$
D_{g}=\sum_{j=1}^{S}\left(\frac{\partial g}{\partial q_{j}} \frac{\partial}{\partial p_{j}}-\frac{\partial g}{\partial p_{j}} \frac{\partial}{\partial q_{j}}\right) \equiv \sum_{i=1}^{2 S} \alpha_{i}(g) \frac{\partial}{\partial \pi_{i}}
$$

物理代写|理论力学作业代写Theoretical Mechanics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。