如果你也在 怎样代写理论力学Theoretical Mechanics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。理论力学Theoretical Mechanics是一组密切相关的经典力学的替代公式。它是由许多科学家和数学家在18世纪及以后,在牛顿力学之后发展起来的。由于牛顿力学考虑的是运动的矢量,特别是系统中各组成部分的加速度、动量、力,因此由牛顿定律和欧拉定律所支配的力学的另一个名称是矢量力学。
理论力学Theoretical Mechanics使用代表系统整体的运动标量属性–通常是其总动能和势能–而不是牛顿对单个粒子的矢量力。运动方程是由标量通过一些关于标量变化的基本原理推导出来的。分析力学使用代表系统整体的运动标量属性–通常是其总动能和势能–而不是牛顿对单个粒子的矢量力。运动方程是由标量通过一些关于标量变化的基本原理推导出来的。
my-assignmentexpert™ 理论力学Theoretical Mechanics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的理论力学Theoretical Mechanics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此理论力学Theoretical Mechanics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在物理physics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的理论力学Theoretical Mechanics代写服务。我们的专家在物理physics代写方面经验极为丰富,各种理论力学Theoretical Mechanics相关的作业也就用不着 说。
我们提供的理论力学Theoretical Mechanics及其相关学科的代写,服务范围广, 其中包括但不限于:
物理代写|理论力学作业代写Theoretical Mechanics代考|Modified Hamilton’s Principle
A weighty advantage, among others, of Hamilton’s principle considered in Sect. $1.3$ lies in the fact that it is applicable also to systems which are not of typical mechanical nature. We now want to reformulate it in such a way that the equivalence to the canonical equations becomes evident. For this purpose we briefly recall the essential elements of this principle. It states that the system movement always takes place such that the action functional
$$
S{\mathbf{q}(t)}=\int_{t_{1}}^{t_{2}} L(\mathbf{q}(t), \dot{\mathbf{q}}(t), t) d t
$$
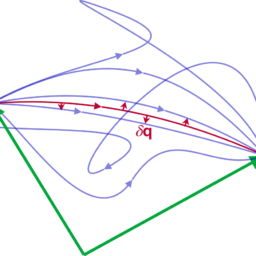
becomes extremal on the set $M$ of the admitted configuration paths $\mathbf{q}(t)$ (Fig. 2.5),
$$
M \equiv\left{\mathbf{q}(t): \mathbf{q}\left(t_{1}\right)=\mathbf{q}{\mathrm{a}}, \mathbf{q}\left(t{2}\right)=\mathbf{q}{\mathrm{e}}\right} $$ for the actual path we are interested in: $$ (\delta S){\mathrm{M}} \stackrel{!}{=} 0
$$
物理代写|理论力学作业代写Theoretical Mechanics代考|Principle of Least Action
A further principle dates back to Maupertuis (1747) which has the same explanatory power as Hamilton’s principle. We will formulate it and prove its equivalence to the principle of Hamilton. Let us define:
Definition 2.3.1 ‘action’
$$
A=\int_{t_{1}}^{t_{2}} \sum_{j=1}^{S} p_{j} \dot{q}_{j} d t
$$
$A$ has the dimension ‘energy ‘time’. We express the ‘principle of least action’ as
$$
H=T+V=E=\text { const }
$$
it holds:
$$
\Delta A=\Delta \int_{t_{1}}^{t_{2}} d t \sum_{j=1}^{S} p_{j} \dot{q}{j}=0 $$ for the path in phase space actually chosen by the system. In order to correctly understand the theorem the new path variation $\Delta$ must be defined very carefully. In Hamilton’s principle (1.121) and (2.55), respectively, the paths which are admitted to the $\boldsymbol{\delta}$-variation arise from each other by the virtual displacements $\delta q$, which are performed at constant time. All paths assume for $t{1}, t_{2}$ the same end-configurations $q_{\mathrm{a}}, q_{\mathrm{e}}$. Common characteristic of all paths is thus the same pass-through time. For the
$\Delta$-variation,
too, the end-configurations shall be fixed:
$$
\Delta \mathbf{q}{\mathrm{a}}=\Delta \mathbf{q}{\mathrm{e}}=0
$$
The common characteristic of all paths admitted to this variation is now an identical Hamilton function:
$$
\Delta H=0 \Longleftrightarrow \Delta T=-\Delta V .
$$
物理代写|理论力学作业代写THEORETICAL MECHANICS代考|Fermat’s Principle
We want to apply the just discussed principle of least action further to a special case, namely to the
force-free motion $\Longleftrightarrow V=$ const
Since already $H=T+V=$ const was presumed it now even holds:
$$
\sum_{j=1}^{S} p_{j} \dot{q}{j}=H+L=2 T=\text { const } $$ On all the admitted paths the kinetic energy is therefore a conserved quantity. The principle (2.65) then simplifies to the statement: $$ \Delta \int{t_{1}}^{t_{2}} d t=\Delta\left(t_{2}-t_{1}\right) \stackrel{!}{=} 0
$$
In case of a force-free movement the system always seeks the path for which the pass-through time becomes extremal (minimal). That is the
principle of least time
first formulated by Fermat that is known in geometrical optics as Fermat’s principle. It says there that the light ray moves between two points of space such that the pass-through time becomes minimal. This principle can successfully be applied, for instance, to light refraction leading to the law of reflexion.
If we specialize furtheron to a
force-free mass point
then we have because of $T=$ const even $v=$ const and (2.81) reads:
$$
\Delta \int_{t_{1}}^{t_{2}} d t=\Delta \int_{t_{1}}^{t_{2}} v d t=\Delta \int_{1}^{2} d s \stackrel{!}{=} 0
$$
This is the principle of the shortest path
It determines the force-free movement of a mass point on a curved plane along a socalled geodesic line. In general one understands by this the shortest line connecting two points on a given plane.
理论力学代写
物理代写|理论力学作业代写THEORETICAL MECHANICS代考|MODIFIED HAMILTON’S PRINCIPLE
汉密尔顿原则在 Sect.1.3在于它也适用于非典型机械性质的系统。我们现在想以这样一种方式重新表述它,使得与规范方程的等价性变得明显。为此,我们简要回顾这一原则的基本要素。它指出系统运动总是发生,使得动作功能
小号q(吨)=∫吨1吨2大号(q(吨),q˙(吨),吨)d吨
在集合上变得极值米允许的配置路径q(吨) F一世G.2.5,
$$
M \equiv\left{\mathbf{q}(t): \mathbf{q}\left(t_{1}\right)=\mathbf{q}{\mathrm{a}}, \mathbf{q}\left(t{2}\right)=\mathbf{q}{\mathrm{e}}\right} $$ for the actual path we are interested in: $$ (\delta S){\mathrm{M}} \stackrel{!}{=} 0
$$
物理代写|理论力学作业代写THEORETICAL MECHANICS代考|PRINCIPLE OF LEAST ACTION
另一个原则可以追溯到 Maupertuis1747它具有与汉密尔顿原理相同的解释力。我们将制定它并证明它与汉密尔顿原理的等价性。让我们定义:
定义 2.3.1 ‘动作’
一种=∫吨1吨2∑j=1小号pjq˙jd吨
一种具有维度’能量’时间’。我们将“最少行动原则”表示为H=吨+五=和= 常量
它持有:
$$
\Delta A=\Delta \int_{t_{1}}^{t_{2}} dt \sum_{j=1}^{S} p_{j} \dot{q} {j} =0 $$ 表示系统实际选择的相空间中的路径。为了正确理解定理新的路径变化Δ必须非常仔细地定义。在汉密尔顿原理中1.121和2.55,分别是允许进入的路径d-通过虚拟位移彼此产生变化dq,这是在恒定时间执行的。所有路径都假定为 $$
H=T+V=E=\text { const }
$$
it holds:
$$
\Delta A=\Delta \int_{t_{1}}^{t_{2}} d t \sum_{j=1}^{S} p_{j} \dot{q}{j}=0 $$ for the path in phase space actually chosen by the system. In order to correctly understand the theorem the new path variation $\Delta$ must be defined very carefully. In Hamilton’s principle (1.121) and (2.55), respectively, the paths which are admitted to the $\boldsymbol{\delta}$-variation arise from each other by the virtual displacements $\delta q$, which are performed at constant time. All paths assume for $t{1}, t_{2}$ the same end-configurations $q_{\mathrm{a}}, q_{\mathrm{e}}$. Common characteristic of all paths is thus the same pass-through time. For the
$\Delta$-variation,
too, the end-configurations shall be fixed:
$$
\Delta \mathbf{q}{\mathrm{a}}=\Delta \mathbf{q}{\mathrm{e}}=0
$$
The common characteristic of all paths admitted to this variation is now an identical Hamilton function:
$$
\Delta H=0 \Longleftrightarrow \Delta T=-\Delta V .
$$
物理代写|理论力学作业代写THEORETICAL MECHANICS代考|FERMAT’S PRINCIPLE
我们想将刚才讨论的最小作用原理进一步应用于一种特殊情况,即无力
运动⟺五=const
因为已经H=吨+五=const 被认为现在甚至成立:
$$
\sum_{j=1}^{S} p_{j} \dot{q}{j}=H+L=2 T=\text { const } $$ On all the admitted paths the kinetic energy is therefore a conserved quantity. The principle (2.65) then simplifies to the statement: $$ \Delta \int{t_{1}}^{t_{2}} d t=\Delta\left(t_{2}-t_{1}\right) \stackrel{!}{=} 0
$$
In case of a force-free movement the system always seeks the path for which the pass-through time becomes extremal (minimal). That is the
principle of least time
first formulated by Fermat that is known in geometrical optics as Fermat’s principle. It says there that the light ray moves between two points of space such that the pass-through time becomes minimal. This principle can successfully be applied, for instance, to light refraction leading to the law of reflexion.
If we specialize furtheron to a
force-free mass point
then we have because of $T=$ const even $v=$ const and (2.81) reads:
$$
\Delta \int_{t_{1}}^{t_{2}} d t=\Delta \int_{t_{1}}^{t_{2}} v d t=\Delta \int_{1}^{2} d s \stackrel{!}{=} 0
$$
这是最短路径原理
它决定了一个质点在曲面上沿所谓的测地线的无力运动。一般来说,人们可以理解为连接给定平面上两点的最短线。

物理代写|理论力学作业代写Theoretical Mechanics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。