如果你也在 怎样代写matlab这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。matlab是由MathWorks公司开发的一种专有的多范式编程语言和数字计算环境。MATLAB允许进行矩阵操作、绘制函数和数据、实现算法、创建用户界面以及与用其他语言编写的程序对接。
matlab尽管MATLAB主要用于数值计算,但一个可选的工具箱使用MuPAD符号引擎,允许访问符号计算能力。一个额外的软件包,Simulink,为动态和嵌入式系统增加了图形化的多域仿真和基于模型的设计。截至2020年,MATLAB在全球拥有超过400万用户。他们来自工程、科学和经济的各种背景。
my-assignmentexpert™ matlab作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的matlab作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此matlab作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在数学Mathematics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的matlab代写服务。我们的专家在数学Mathematics代写方面经验极为丰富,各种matlab相关的作业也就用不着 说。
我们提供的matlab及其相关学科的代写,服务范围广, 其中包括但不限于:
数学代写|matlab代写|Introduction
A common problem encountered in engineering analysis is this: given a function $f(x)$, determine the values of $x$ for which $f(x)=0$. The solutions (values of $x$ ) are known as the roots of the equation $f(x)=0$, or the zeroes of the function $f(x)$.
Before proceeding further, it might be helpful to review the concept of a function. The equation
$$
y=f(x)
$$
contains three elements: an input value $x$, an output value $y$ and the rule $f$ for computing $y$. The function is said to be given if the rule $f$ is specified. In numerical computing the rule is invariably a computer algorithm. It may be a function statement, such as
$$
f(x)=\cosh (x) \cos (x)-1
$$
or a complex procedure containing hundreds or thousands of lines of code. As long as the algorithm produces an output $y$ for each input $x$, it qualifies as a function.
The roots of equations may be real or complex. The complex roots are seldom computed, since they rarely have physical significance. An exception is the polynomial equation
$$
a_{1} x^{n}+a_{2} x^{n-1}+\cdots+a_{n} x+a_{n+1}=0
$$
where the complex roots may be meaningful (as in the analysis of damped vibrations, for example). For the time being, we will concentrate on finding the real roots of equations. Complex zeroes of polynomials are treated near the end of this chapter.
数学代写|matlab代写|Incremental Search Method
The approximate locations of the roots are best determined by plotting the function. Often a very rough plot, based on a few points, is sufficient to give us reasonable starting values. Another useful tool for detecting and bracketing roots is the incremental search method. It can also be adapted for computing roots, but the effort would not be worthwhile, since other methods described in this chapter are more efficient for that.
The basic idea behind the incremental search method is simple: if $f\left(x_{1}\right)$ and $f\left(x_{2}\right)$ have opposite signs, then there is at least one root in the interval $\left(x_{1}, x_{2}\right)$. If the interval is small enough, it is likely to contain a single root. Thus the zeroes of $f(x)$ can be detected by evaluating the function at intervals $\Delta x$ and looking for change in sign. There are several potential problems with the incremental search method:
- It is possible to miss two closely spaced roots if the search increment $\Delta x$ is larger than the spacing of the roots.
- A double root (two roots that coincide) will not be detected.
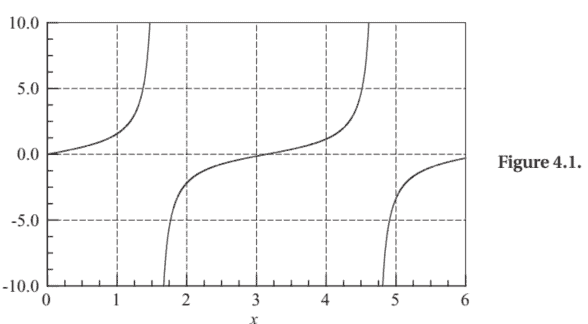
- Certain singularities of $f(x)$ can be mistaken for roots. For example, $f(x)=\tan x$ changes sign at $x=\pm \frac{1}{2} n \pi, n=1,3,5, \ldots$, as shown in Fig. 4.1. However, these locations are not true zeroes, since the function does not cross the $x$-axis.
数学代写|MATLAB代写|Method of Bisection
After a root of $f(x)=0$ has been bracketed in the interval $\left(x_{1}, x_{2}\right)$, several methods can be used to close in on it. The method of bisection accomplishes this by successively halving the interval until it becomes sufficiently small. This technique is also known as the interval halving method. Bisection is not the fastest method available for computing roots, but it is the most reliable. Once a root has been bracketed, bisection will always close in on it.
The method of bisection uses the same principle as incremental search: if there is a root in the interval $\left(x_{1}, x_{2}\right)$, then $f\left(x_{1}\right) \cdot f\left(x_{2}\right)<0$. In order to halve the interval, we compute $f\left(x_{3}\right)$, where $x_{3}=\frac{1}{2}\left(x_{1}+x_{2}\right)$ is the midpoint of the interval. If $f\left(x_{2}\right) \cdot f\left(x_{3}\right)<$ 0 , then the root must be in $\left(x_{2}, x_{3}\right)$ and we record this by replacing the original bound $x_{1}$ by $x_{3}$. Otherwise, the root lies in $\left(x_{1}, x_{3}\right)$, in which case $x_{2}$ is replaced by $x_{3}$. In either case, the new interval $\left(x_{1}, x_{2}\right)$ is half the size of the original interval. The bisection is repeated until the interval has been reduced to a small value $\varepsilon$, so that
$$
\left|x_{2}-x_{1}\right| \leq \varepsilon
$$
It is easy to compute the number of bisections required to reach a prescribed $\varepsilon$. The original interval $\Delta x$ is reduced to $\Delta x / 2$ after one bisection, $\Delta x / 2^{2}$ after two bisections and after $n$ bisections it is $\Delta x / 2^{n}$. Setting $\Delta x / 2^{n}=\varepsilon$ and solving for $n$, we get
$$
n=\frac{\ln (|\Delta x| / \varepsilon)}{\ln 2}
$$

matlab代写
数学代写|MATLAB代写|INTRODUCTION
工程分析中遇到的一个常见问题是:给定一个函数F(X),确定的值X为此F(X)=0. 解决方案在一种l在和s这F$X$被称为方程的根F(X)=0, 或函数的零点F(X).
在继续之前,回顾一下函数的概念可能会有所帮助。方程
是=F(X)
包含三个元素:一个输入值X, 一个输出值是和规则F用于计算是. 如果规则是给定的,则称该函数F被指定。在数值计算中,规则总是一种计算机算法。它可能是一个函数语句,例如
F(X)=科什(X)因(X)−1
或包含数百或数千行代码的复杂过程。只要算法产生输出是对于每个输入X,它有资格作为一个函数。
方程的根可以是实数或复数。很少计算复杂的根,因为它们很少具有物理意义。一个例外是多项式方程
一种1Xn+一种2Xn−1+⋯+一种nX+一种n+1=0
其中复根可能有意义一种s一世n吨H和一种n一种l是s一世s这Fd一种米p和d在一世br一种吨一世这ns,F这r和X一种米pl和. 目前,我们将专注于寻找方程的真正根。多项式的复零点将在本章结尾处处理。
数学代写|MATLAB代写|INCREMENTAL SEARCH METHOD
根的近似位置最好通过绘制函数来确定。通常,基于几个点的非常粗略的情节足以为我们提供合理的起始值。另一个用于检测和包围根的有用工具是增量搜索方法。它也可以适用于计算根,但这种努力是不值得的,因为本章描述的其他方法对此更有效。
增量搜索方法背后的基本思想很简单:如果F(X1)和F(X2)有相反的符号,则区间内至少有一个根(X1,X2). 如果间隔足够小,则很可能包含单个根。因此零F(X)可以通过每隔一段时间评估函数来检测ΔX并寻找符号的变化。增量搜索方法存在几个潜在问题:
- 如果搜索增量,可能会错过两个紧密间隔的根ΔX大于根间距。
- 双根吨在这r这这吨s吨H一种吨C这一世nC一世d和不会被检测到。
- 的某些奇点F(X)可能被误认为是根。例如,F(X)=棕褐色X更改签名X=±12n圆周率,n=1,3,5,…,如图 4.1 所示。然而,这些位置不是真正的零点,因为函数不跨越X-轴。
数学代写|MATLAB代写|METHOD OF BISECTION
一个根之后F(X)=0已括在区间内(X1,X2),可以使用几种方法来关闭它。二分法通过将间隔连续减半直到它变得足够小来实现这一点。这种技术也称为间隔减半法。二分法不是计算根的最快方法,但它是最可靠的。一旦根被括号括起来,二分法将始终关闭它。
二分法使用与增量搜索相同的原理:如果区间中有根(X1,X2), 然后F(X1)⋅F(X2)<0. 为了将间隔减半,我们计算F(X3), 在哪里X3=12(X1+X2)是区间的中点。如果F(X2)⋅F(X3)<0 ,那么根必须在(X2,X3)我们通过替换原始边界来记录这一点X1经过X3. 否则,根源在于(X1,X3), 在这种情况下X2被替换为X3. 在任何一种情况下,新的间隔(X1,X2)是原始区间大小的一半。重复二等分,直到间隔减小到一个小值e, 以便
|X2−X1|≤e
很容易计算达到规定所需的二等分数e. 原始区间ΔX减少到ΔX/2一等分后,ΔX/22两等分之后和之后n它是二等分ΔX/2n. 环境ΔX/2n=e并解决n,我们得到
n=ln(|ΔX|/e)ln2

数学代写|matlab代写 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。