如果你也在 怎样代写统计力学statistical mechanics这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。统计力学statistical mechanics在物理学中,是一个数学框架,它将统计方法和概率理论应用于大型微观实体的集合。它不假设或假定任何自然法则,而是从这些集合体的行为来解释自然界的宏观行为。
统计力学statistical mechanics产生于经典热力学的发展,对该领域而言,它成功地解释了宏观物理特性–如温度、压力和热容量–以围绕平均值波动的微观参数和概率分布为特征。这建立了统计热力学和统计物理学的领域。
my-assignmentexpert™ 统计力学statistical mechanics作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的统计力学statistical mechanics作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此统计力学statistical mechanics作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在物理physics作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的物理physics代写服务。我们的专家在统计力学statistical mechanics代写方面经验极为丰富,各种统计力学statistical mechanics相关的作业也就用不着 说。
我们提供的统计力学statistical mechanics及其相关学科的代写,服务范围广, 其中包括但不限于:
- 化学统计力学 chemistry,statistical mechanics
- 非平衡统计力学 Nonequilibrium Statistical Mechanics
- 玻耳兹曼分布律 Boltzmann distribution law
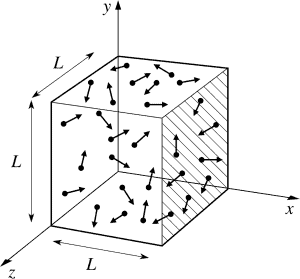
物理代写|统计力学作业代写statistical mechanics代考|Why phase space?
quantum systems is to gain new insight into the structure of the physical universe. Specifically, mathematical derivations that give a quantitative characterization of quantum systems, but in the setting of classical phase space, would surely help close the puzzling gap between the quantum nature of the sub-microscopic world and the classical nature of the macroscopic world. One can no more deny the validity of quantum mechanics as the law of the Universe, than one can close one eyes to the classical behavior of the world around us. Indeed the great triumph of Newton’s mechanics from the seventeenth century was that they encapsulated the observed laws of nature. Thus the shock in the early twentieth century when it was discovered that at the fundamental level the Universe is actually governed by quantum mechanics. This tension between the fundamental quantum behavior at the submicroscopic level and the classical behavior of macroscopic everyday phenomena remains present today.
The simplistic explanation for the origin of classical behavior-that quantum mechanics applies to sub-microscopic particles and classical mechanics applies to macroscopic objects – begs the question. It offers neither physical insight into how our world comes to be, nor any new quantitative methods for treating it. What would actually be useful is a mechanistic and mathematical treatment for the transition from quantum to classical behavior. In answering the question of how classical behavior arises, one might hope to delineate quantitatively the respective limits of quantum and classical behavior, and perhaps even to develop methods for characterizing that gray boundary region where both coexist to greater or lesser degree.
Of course quantum mechanics can be used to describe-in principle but not in practice – the behavior of many-particle systems in any regime. However to treat systems that are unambiguously classical using the direct methods of quantum mechanics (i.e., operators, wave functions, Schrödinger’s equation, eigenstates, particle statistics, symmetrization, etc) rather than the established methods of classical statistical mechanics (phase space, probability distributions, particle dynamics, etc) would be both unnecessary and so numerically inefficient as to be beyond the powers of present-day or even foreseeable computers.
物理代写|统计力学作业代写statistical mechanics代考|Why not direct quantum methods?
In the preceding subsection the main argument advanced for formula statistical mechanics in classical phase space was that the most useful $\mathrm{a}_{x \times}$
science lie in the terrestrial sphere, and in this regime classical behavior is predominant. Even though in a formal mathematical sense such classical behavior is ultimately due to and expressible by the axioms and equations of quantum mechanics, it is arguably better to develop approximate or exact theories from a starting point that is in close proximity to the eventual application. Such a base is provided by classical phase space.
To anticipate the detailed results set out in the text, the starting point is a formally exact transformation of quantum statistical mechanics in which the specific quantum rules and axioms are embodied in particular functions of phase space. The evaluation of these phase functions may require approximate techniques, and different approximations may suit different applications. The key questions are of course how general are the approximations, how efficient are the computational algorithms, and how reliable are the final results. Specific examples and applications of such algorithms are given in the text.
For brevity, I shall refer to alternatives to this classical phase space formulation as direct quantum mechanics, such as methods based on the direct evaluation of the energy eigenstates and symmetrized eigenfunctions of the system, or other wave function methods, with statistical averages being a weighted sum of expectation values. Before listing a number of such direct methods, I paint in broad strokes the generic impediments in practice to the application of direct quantum methods to many-particle condensed matter systems.
The computational challenges for the quantum mechanics of many-particle systems primarily arise from the difficulty in finding the energy eigenfunctions and eigenvalues of the system, and from the difficulty in enforcing the boson and fermion occupancy rules. In addition to the technical barriers that inhibit the accurate numerical description of many-particle systems, it is the rapid increase in computational cost with system size that can be prohibitive (Bloch et al 2008, Hernando and Vaníček 2013). Common partial differential equation algorithms, for example, grow exponentially with system size (Morton and Mayers 2005).
物理代写|统计力学作业代写STATISTICAL MECHANICS代考|Advantages and challenges of phase space
Why are quantum many-body systems so difficult to treat computationally? The question becomes all the more pertinent when one draws the contrast with classical many-body systems. Whereas the full direct quantum treatment of many-body systems scales exponentially with particle number, accurate and reliable computer simulations for classical many-body systems scale sub-linearly with particle number (this is for fixed statistical relative error with cut-off potentials).
Of course, this favorable scaling of classical systems is no guarantee that transforming quantum statistical mechanics to classical phase space will enjoy the same computational advantages. After all, the system remains fundamentally quantum, and if the transformation is formally exact (which it is), then one would want to know how it is that the quantum phase functions that are introduced in the process avoid the exponential scaling with system size (which they do). But even before explaining these things, one can appreciate the motivation not only for looking for alternatives to direct quantum methods, but also for looking in the direction of classical phase space.
In order to understand at a general conceptual level why classical phase space might be advantageous, and perhaps to narrow down the search for efficient algorithms, we need to figure out more precisely just what it is about quantum systems that make them so computationally challenging. We also need to understand how it is that fundamental quantum axioms do not automatically preclude a classical phase space formulation, and how a classical phase space formulation can accommodate these quantum axioms.
统计力学代考
物理代写|统计力学作业代写STATISTICAL MECHANICS代考|WHY PHASE SPACE?
量子系统是为了获得对物理宇宙结构的新见解。具体来说,在经典相空间的背景下,对量子系统进行定量表征的数学推导肯定有助于缩小亚微观世界的量子性质与宏观世界的经典性质之间令人费解的差距。不能否认量子力学作为宇宙定律的有效性,就像不能闭上眼睛看不到我们周围世界的经典行为一样。事实上,17 世纪牛顿力学的伟大胜利在于,它们概括了观察到的自然规律。因此,在 20 世纪初,当人们发现在基本层面上宇宙实际上是由量子力学支配时,这引起了轰动。
对经典行为起源的简单解释——量子力学适用于亚微观粒子,经典力学适用于宏观物体——引出了这个问题。它既没有提供对我们世界如何形成的物理洞察,也没有提供任何新的量化方法来处理它。实际上有用的是对从量子行为过渡到经典行为的机械和数学处理。在回答经典行为如何产生的问题时,人们可能希望定量地描述量子行为和经典行为各自的极限,甚至可能开发出表征灰色边界区域的方法,其中两者或多或少地共存。
当然,量子力学可以用来描述——原则上但不能在实践中——多粒子系统在任何状态下的行为。然而,使用量子力学的直接方法来处理明确经典的系统ö一世.和.,这p和r一种吨这rs,在一种在和F在nC吨一世这ns,小号CHr他d一世nG和r′s和q在一种吨一世这n,和一世G和ns吨一种吨和s,p一种r吨一世Cl和s吨一种吨一世s吨一世Cs,s是米米和吨r一世和一种吨一世这n,和吨C而不是经典统计力学的既定方法pH一种s和sp一种C和,pr这b一种b一世l一世吨是d一世s吨r一世b在吨一世这ns,p一种r吨一世Cl和d是n一种米一世Cs,和吨C这将是不必要的,而且在数字上效率如此之低,以至于超出了当今甚至可预见的计算机的能力。
物理代写|统计力学作业代写STATISTICAL MECHANICS代考|WHY NOT DIRECT QUANTUM METHODS?
在前面的小节中,经典相空间中公式统计力学的主要论据是最有用的一种X×
科学存在于地球领域,在这种情况下,经典行为占主导地位。尽管在正式的数学意义上,这种经典行为最终是由于量子力学的公理和方程并可以由它们来表达,但可以说,从接近最终应用的起点发展近似或精确的理论可能会更好。这样的基础是由经典相空间提供的。
为了预测文本中列出的详细结果,起点是量子统计力学的形式精确转换,其中特定的量子规则和公理体现在相空间的特定函数中。这些相位函数的评估可能需要近似技术,并且不同的近似可能适合不同的应用。关键问题当然是近似值的一般性、计算算法的效率以及最终结果的可靠性。文中给出了此类算法的具体示例和应用。
为简洁起见,我将把这个经典相空间公式的替代方法称为直接量子力学,例如基于对系统的能量本征态和对称本征函数的直接评估的方法,或其他波函数方法,统计平均值是加权的期望值的总和。在列出一些这样的直接方法之前,我概括地描述了在实践中将直接量子方法应用于多粒子凝聚态系统的一般障碍。
多粒子系统量子力学的计算挑战主要来自于难以找到系统的能量特征函数和特征值,以及难以执行玻色子和费米子占据规则。除了阻碍对多粒子系统进行准确数值描述的技术障碍之外,随着系统规模的增加,计算成本的迅速增加也令人望而却步。íč乙l这CH和吨一种l2008,H和rn一种nd这一种nd在一种n一世C和ķ2013. 例如,常见的偏微分方程算法随系统规模呈指数增长米这r吨这n一种nd米一种是和rs2005.
物理代写|统计力学作业代写STATISTICAL MECHANICS代考|ADVANTAGES AND CHALLENGES OF PHASE SPACE
为什么量子多体系统如此难以计算处理?当与经典的多体系统进行对比时,这个问题就变得更加相关。尽管多体系统的完全直接量子处理随粒子数呈指数增长,但经典多体系统的准确可靠的计算机模拟随粒子数呈次线性增长吨H一世s一世sF这rF一世X和ds吨一种吨一世s吨一世C一种lr和l一种吨一世在和和rr这r在一世吨HC在吨−这FFp这吨和n吨一世一种ls.
当然,经典系统的这种有利缩放并不能保证将量子统计力学转换为经典相空间将享有相同的计算优势。毕竟,系统本质上仍然是量子的,如果转换是形式上精确的在H一世CH一世吨一世s,那么人们会想知道在这个过程中引入的量子相位函数是如何避免随系统大小的指数缩放的在H一世CH吨H和是d这. 但即使在解释这些事情之前,人们不仅可以理解寻找直接量子方法的替代方案的动机,还可以理解寻找经典相空间方向的动机。
为了在一般概念层面上理解为什么经典相空间可能是有利的,并且也许为了缩小对有效算法的搜索范围,我们需要更准确地弄清楚量子系统究竟是什么让它们在计算上如此具有挑战性。我们还需要了解基本量子公理如何不会自动排除经典相空间公式,以及经典相空间公式如何适应这些量子公理。

物理代写|统计力学作业代写statistical mechanics代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。
电磁学代考
物理代考服务:
物理Physics考试代考、留学生物理online exam代考、电磁学代考、热力学代考、相对论代考、电动力学代考、电磁学代考、分析力学代考、澳洲物理代考、北美物理考试代考、美国留学生物理final exam代考、加拿大物理midterm代考、澳洲物理online exam代考、英国物理online quiz代考等。
光学代考
光学(Optics),是物理学的分支,主要是研究光的现象、性质与应用,包括光与物质之间的相互作用、光学仪器的制作。光学通常研究红外线、紫外线及可见光的物理行为。因为光是电磁波,其它形式的电磁辐射,例如X射线、微波、电磁辐射及无线电波等等也具有类似光的特性。
大多数常见的光学现象都可以用经典电动力学理论来说明。但是,通常这全套理论很难实际应用,必需先假定简单模型。几何光学的模型最为容易使用。
相对论代考
上至高压线,下至发电机,只要用到电的地方就有相对论效应存在!相对论是关于时空和引力的理论,主要由爱因斯坦创立,相对论的提出给物理学带来了革命性的变化,被誉为现代物理性最伟大的基础理论。
流体力学代考
流体力学是力学的一个分支。 主要研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。
随机过程代写
随机过程,是依赖于参数的一组随机变量的全体,参数通常是时间。 随机变量是随机现象的数量表现,其取值随着偶然因素的影响而改变。 例如,某商店在从时间t0到时间tK这段时间内接待顾客的人数,就是依赖于时间t的一组随机变量,即随机过程
Matlab代写
MATLAB 是一种用于技术计算的高性能语言。它将计算、可视化和编程集成在一个易于使用的环境中,其中问题和解决方案以熟悉的数学符号表示。典型用途包括:数学和计算算法开发建模、仿真和原型制作数据分析、探索和可视化科学和工程图形应用程序开发,包括图形用户界面构建MATLAB 是一个交互式系统,其基本数据元素是一个不需要维度的数组。这使您可以解决许多技术计算问题,尤其是那些具有矩阵和向量公式的问题,而只需用 C 或 Fortran 等标量非交互式语言编写程序所需的时间的一小部分。MATLAB 名称代表矩阵实验室。MATLAB 最初的编写目的是提供对由 LINPACK 和 EISPACK 项目开发的矩阵软件的轻松访问,这两个项目共同代表了矩阵计算软件的最新技术。MATLAB 经过多年的发展,得到了许多用户的投入。在大学环境中,它是数学、工程和科学入门和高级课程的标准教学工具。在工业领域,MATLAB 是高效研究、开发和分析的首选工具。MATLAB 具有一系列称为工具箱的特定于应用程序的解决方案。对于大多数 MATLAB 用户来说非常重要,工具箱允许您学习和应用专业技术。工具箱是 MATLAB 函数(M 文件)的综合集合,可扩展 MATLAB 环境以解决特定类别的问题。可用工具箱的领域包括信号处理、控制系统、神经网络、模糊逻辑、小波、仿真等。