如果你也在 怎样代写数字电路DIGITAL CIRCUIT这个学科遇到相关的难题,请随时右上角联系我们的24/7代写客服。数字电路DIGITAL CIRCUIT是电子学的一个领域,涉及数字信号的研究和使用或产生数字信号的设备工程。这与模拟电子学和模拟信号相反。
数字电路DIGITAL CIRCUIT电路通常由逻辑门的大型组件制成,通常被封装在集成电路中。复杂的设备可能有简单的布尔逻辑功能的电子表示。
my-assignmentexpert™ 数字电路DIGITAL CIRCUIT作业代写,免费提交作业要求, 满意后付款,成绩80\%以下全额退款,安全省心无顾虑。专业硕 博写手团队,所有订单可靠准时,保证 100% 原创。my-assignmentexpert™, 最高质量的数字电路DIGITAL CIRCUIT作业代写,服务覆盖北美、欧洲、澳洲等 国家。 在代写价格方面,考虑到同学们的经济条件,在保障代写质量的前提下,我们为客户提供最合理的价格。 由于统计Statistics作业种类很多,同时其中的大部分作业在字数上都没有具体要求,因此数字电路DIGITAL CIRCUIT作业代写的价格不固定。通常在经济学专家查看完作业要求之后会给出报价。作业难度和截止日期对价格也有很大的影响。
想知道您作业确定的价格吗? 免费下单以相关学科的专家能了解具体的要求之后在1-3个小时就提出价格。专家的 报价比上列的价格能便宜好几倍。
my-assignmentexpert™ 为您的留学生涯保驾护航 在信息Information作业代写方面已经树立了自己的口碑, 保证靠谱, 高质且原创的数字电路DIGITAL CIRCUIT代写服务。我们的专家在信息Information代写方面经验极为丰富,各种数字电路DIGITAL CIRCUIT相关的作业也就用不着 说。
我们提供的数字电路DIGITAL CIRCUIT及其相关学科的代写,服务范围广, 其中包括但不限于:
调和函数 harmonic function
椭圆方程 elliptic equation
抛物方程 Parabolic equation
双曲方程 Hyperbolic equation
非线性方法 nonlinear method
变分法 Calculus of Variations
几何分析 geometric analysis
偏微分方程数值解 Numerical solution of partial differential equations
信号代写|数字电路作业代写digital circuit代考|FIXED-BIAS CIRCUI
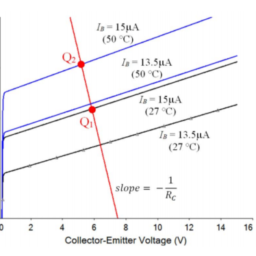
One method of biasing a transistor to operate at a desired Q-point is illustrated in Figure $3.18 \mathrm{a}$ which shows the fixed-bias circuit (sometimes called the base-bias circuit). It is convenient to use the forward-active model of the npn BJT as shown in Figure $3.18 \mathrm{~b}$ for analyzing bias circuits.
The collector-emitter voltage $V_{C E}=V_{C}-V_{E}$ is equal to the power supply voltage minus the voltage drop across the collector resistor $R_{C}$. That is:
$$
V_{C E}=V_{C C}-I_{C} R_{C}
$$
where
$$
\begin{aligned}
V_{C E} &=\mathrm{DC} \text { collector-emitter voltage } \
V_{C C} &=\text { collector supply voltage } \
I_{C} &=\mathrm{DC} \text { collector current } \
R_{C} &=\text { load resistance seen from the collector. }
\end{aligned}
$$
Kirchhoff’s Voltage Law applied to the base-emitter loop, yields the following expression for the base current:
$$
I_{B}=\frac{V_{C C}-V_{B E}}{R_{B}} .
$$
Substituting $I_{C}=\beta_{F} I_{B}$ and Equation (3.23) into Equation (3.22), the collector-emitter voltage becomes
$$
V_{C E}=V_{C C}-\beta_{F}\left(\frac{V_{C C}-V_{B E}}{R_{B}}\right) R_{C} .
$$
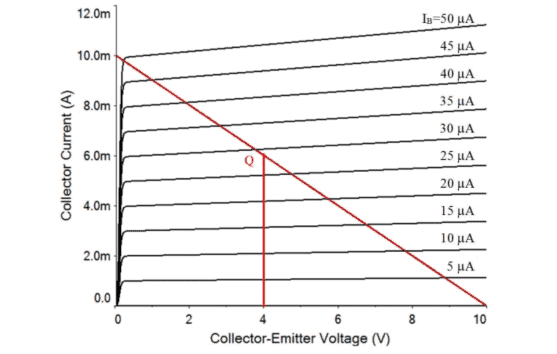
The Q-point is defined by $I_{C}$ and $V_{C E}$ for a specified $I_{B}$.
信号代写|数字电路作业代写digital circuit代考|EMITTER-BIAS CIRCUIT
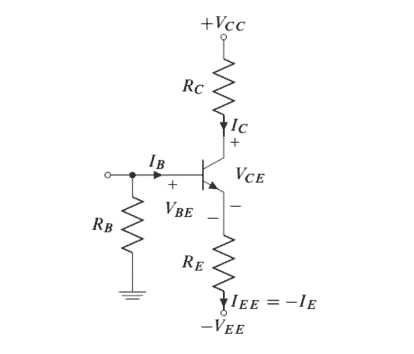
The emitter-bias circuit is often used when two power supplies (positive and negative) are available. In this configuration, shown in Figure $3.27$ the collector current can easily be made to be essentially independent of $\beta_{F}$, making the circuit less sensitive to variations in $\beta_{F}$ due to temperature or transistor replacement.
To find $I_{C}$, the KVL equation for the base-emitter loop is found,
$$
\begin{aligned}
V_{E E} &=V_{B E}+I_{B} R_{B}+I_{E E} R_{E} \
&=V_{B E}+I_{C}\left[\frac{R_{B}}{\beta_{F}}+\left(\frac{\beta_{F}+1}{\beta_{F}}\right) R_{E}\right] .
\end{aligned}
$$
信号代写|数字电路作业代写DIGITAL CIRCUIT代考|SELF-BIAS CIRCUIT
The analysis of the diagram of Figure $3.31$ is similar to that of the fixed-bias circuit. Applying KVL on the base-emitter loop,
$$
\begin{aligned}
V_{B B} &=I_{B} R_{B}+V_{B E}+I_{E E} R_{E} \
&=V_{B E}+I_{C}\left[\frac{R_{B}}{\beta_{F}}+\left(\frac{\beta_{F}+1}{\beta_{F}}\right) R_{E}\right] .
\end{aligned}
$$
Solving for the collector current,
$$
\begin{aligned}
I_{C} &=\frac{V_{B B}-V_{B E}}{\frac{R_{B}}{\beta_{F}}+\left(\frac{\beta_{F}+1}{\beta_{F}}\right) R_{E}}=\left(\frac{\beta_{F}}{\beta_{F}+1}\right) \frac{V_{B B}-V_{B E}}{R_{E}+\frac{R_{B}}{\beta_{F}+1}} \
&=\left(\frac{\beta_{F}}{\beta_{F}+1}\right) \frac{\left(\frac{V_{C C} R_{B 2}}{R_{B 1}+R_{B 2}}-V_{B E}\right)}{R_{E}+\frac{R_{B 1} R_{B 2}}{\left(R_{B 1}+R_{B 2}\right)\left(\beta_{F}+1\right)}} .
\end{aligned}
$$
The equation relating $V_{C E}$ to $I_{C}$ (Equation (3.28) repeated as Equation (3.56) below) and the load line analysis are identical to the fixed-bias circuit with emitter feedback,
$$
\begin{aligned}
V_{C E} &=V_{C C}-I_{C} R_{C}-I_{E E} R_{E} \
&=V_{C C}-I_{C}\left(R_{C}+\left(\frac{\beta_{F}+1}{\beta_{F}}\right) R_{E}\right)
\end{aligned}
$$
数字电路代写
信号代写|数字电路作业代写DIGITAL CIRCUIT代考|FIXED-BIAS CIRCUI
图 1 说明了一种偏置晶体管以使其工作在所需 Q 点的方法。3.18一种其中显示了固定偏置电路s这米和吨一世米和sC一种ll和d吨H和b一种s和−b一世一种sC一世rC在一世吨. 使用npn BJT的前向激活模型很方便,如图3.18 b用于分析偏置电路。
集电极-发射极电压在C和=在C−在和等于电源电压减去集电极电阻两端的电压降RC. 那是:
在C和=在CC−一世CRC
在哪里
在C和=DC 集电极-发射极电压 在CC= 集电极电源电压 一世C=DC 集电极电流 RC= 从集电极看到的负载电阻。
基尔霍夫电压定律应用于基极-发射极回路,产生以下基极电流表达式:
一世乙=在CC−在乙和R乙.
替代一世C=bF一世乙和方程3.23进入方程3.22,集电极-发射极电压变为
在C和=在CC−bF(在CC−在乙和R乙)RC.
Q点定义为一世C和在C和对于指定的一世乙.
信号代写|数字电路作业代写DIGITAL CIRCUIT代考|EMITTER-BIAS CIRCUIT
发射极偏置电路通常用于两个电源p这s一世吨一世在和一种ndn和G一种吨一世在和可用。在这个配置中,如图3.27集电极电流可以很容易地制成基本上独立于bF,使电路对变化不太敏感bF由于温度或晶体管更换。
寻找一世C,找到基极-发射极回路的 KVL 方程,
在和和=在乙和+一世乙R乙+一世和和R和 =在乙和+一世C[R乙bF+(bF+1bF)R和].
信号代写|数字电路作业代写DIGITAL CIRCUIT代考|SELF-BIAS CIRCUIT
图的图解分析3.31类似于固定偏置电路。在基极-发射极回路上应用 KVL,
在乙乙=一世乙R乙+在乙和+一世和和R和 =在乙和+一世C[R乙bF+(bF+1bF)R和].
求解集电极电流,
一世C=在乙乙−在乙和R乙bF+(bF+1bF)R和=(bFbF+1)在乙乙−在乙和R和+R乙bF+1 =(bFbF+1)(在CCR乙2R乙1+R乙2−在乙和)R和+R乙1R乙2(R乙1+R乙2)(bF+1).
相关方程在C和到一世C 和q在一种吨一世这n(3.28重复方程3.56下面)和负载线分析与具有发射极反馈的固定偏置电路相同,
在C和=在CC−一世CRC−一世和和R和 =在CC−一世C(RC+(bF+1bF)R和)

信号代写|数字电路作业代写DIGITAL CIRCUIT代考 请认准UprivateTA™. UprivateTA™为您的留学生涯保驾护航。